函数是贯穿中学数学的一条主线,其核心思想在解决各类数学问题中都发挥了至关重要的作用。在开启 Alevel数学学习时,绝大部分学生接触的第一门数学课往往是纯数 P1。在纯数 P1中,学生会学习基本的一元二次函数及其图像,并在此基础上学习如何利用一元二次函数的图像求解一元二次不等式。
这一部分虽说比较基础,但这种将代数方程或代数不等式问题转化成函数图像问题的思想,是具有深刻内涵的。本篇邀请到 G5教研部老师为大家就 Alevel统考和 G5自招考中的函数思想作简要分享,还请详读。
核心思想
专项提升
如前所述,在纯数 P1中,学生还会进一步学习三次函数的图像以及如何用函数图像解决更复杂的方程问题。三次甚至更高次的多项式方程问题,在 G5自招考试 MAT和 TMUA中就会高频出现,可以说是考查的重点。虽说学生在基础课纯数 P1中就已经接触过相关问题,然而根据多年以来 MAT和 TMUA课程的教学经验,多数学生在一开始常常不知道如何处理高次的多项式方程问题。

原版 P1教材中利用函数图像求方程解个数的例题
究其原因,在 Alevel学习过程中遇到的多项式方程或不等式问题时,多项式常常是以因式分解好的形式出现,或者题目会给出方程的其中一个解从而帮助学生顺利自行完成因式分解。然而 G5自招考试中的方程问题就不会有此类明显提示,甚至题目中的多项式难以进行因式分解,因为方程的解很可能不是有理数。
很多学生在遇到多项式方程问题时,第一反应是找到方程的一个解,Alevel试题中有很多也是这个考查模式。这当然是值得尝试的,通过观察和计算看看能否找到方程的某一特殊解,从而简化方程。但是当这样的尝试碰到困难时,很多学生就会感到不知所措。
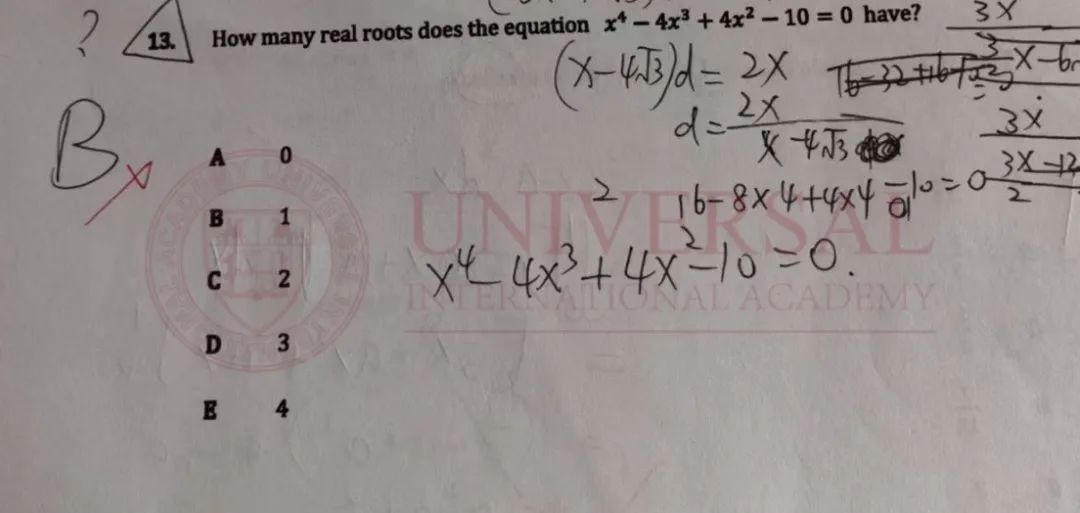
TMUA学员忆忆求解四次方程问题的尝试
在这种时候,G5教研部强调对学生应用微积分研究函数图像问题能力的培养。其实在纯数 P1时,学生就已经学习了如何求解多项式函数的导数,并在 P2阶段学习进一步的知识,包括利用导数研究函数的单调性和求解图像上的极值点。
遗憾的是,原版教材并没有趁热打铁,告诉学生们这些工具可用来解决更一般的多项式方程和不等式问题。在 MAT和 TMUA教学中,G5教研部发现了这一问题,从而针对性地对这一思想方法进行了专项训练。

G5教研部整合自招考讲义中专项知识讲解与习题截图
众所周知,对于一元二次方程,有求根公式和判别式这两个强大工具,所以二次方程是容易求解的。而对于高次的多项式,就没有如此方便的工具了。因式定理的使用要求方程具有特殊解,这是可遇不可求的,在很多 G5自招考的题目中难以发挥用处。
接下来看看微积分方法该如何处理多项式方程解的个数问题:利用导数的工具,可通过求解所有极值点的坐标,画出多项式函数的草图,从而利用方程的解和函数图像的零点进行一一对应,顺利解决问题。以三次方程为例,假如求出来两个极值点,其中一个点的纵坐标大于零,另一个点的纵坐标小于零,那么函数图像必然和 x轴有三个交点,这就是三次方程有三个实数解的等价的几何刻画。

TMUA学员睿睿对三次方程解个数问题的解答
可以说,TMUA和 MAT虽然考查的知识点绝大部分都包含在纯数 P1和 P2的考纲内,但题目的综合性和对数学思想的考查远高于 Alevel试题。
在教学过程中,G5教研部非常注重学生对基础知识的理解。所有的数学方法和思想,想要运用起来,都必须建立在对概念的准确理解上。函数部分,概念本身和各种性质,都是抽象的。
抽象的东西是不好理解的,普遍考生往往容易接受和记住直观的,看得见摸得着的事物。这就是函数思想的作用,把抽象的代数问题具像化,通过研究看得见的函数图像来解决问题。