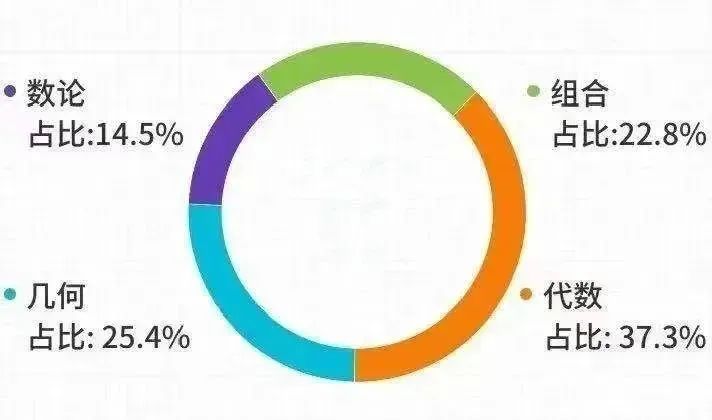
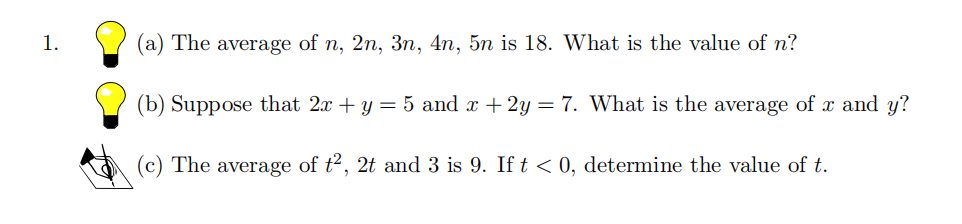针对近年来纯数 P2模块的考点设置复盘,理综教研部将核心考点归为以下类别,分别是代数、圆的方程、指数与对数、等差数列和等比数列、求和定积分和梯形法则以及三角函数的化简问题等。本篇将由理综教研部的 老师就代数、圆的方程以及指数与对数这三大考点为大家分析考生的易错点,助力把握调整方向。
考点解构
攻分有方
『代数』
首先是代数题,该类题型相对基础,重点在于对因式定理和余数定理的考查,也是考生不容失分的题型,其基础分值在 7分左右,此类题型最主要是找到除数,然后令其为 0求出其对应的 x,将其代入原式,若为 factor,则 f(x)=0,若存在余数,则 f(x)=余数,这也是题目的关键所在。但对于 fully factorie类型的题目,理综教研部则会要求考生首先考虑运算过程更加简便的长除法。在考试过程中若出现方法选取上的差异,计算过程则会较为复杂,浪费考试时间,也会容易出现失误。
根据历年真题设置,代数这一章节往往还会有一道证明题的考查,该类题型需要大量文字叙述作答,主要以穷举法 (exhaustion)和反例法 (counter-example)为主,其中穷举法中若数据无限则需分为奇数和偶数两类讨论,很多考生在做这类题型时经常无从下手,其实主要需从问题出发,分别写出奇数和偶数性质,言之有理即可,反例法则只需举出一个反例即可,例如 2022年 6月卷的第 3题,有一个很清晰的标志“false”,非常典型的一道反例法证明,该类题型还有另一个比较常见的标志就是“not”,这就要求考生在作答时若无要求穷举法时,则用相对简单的反例法进行求解即可。

来源:2022年 6月卷 P2模块真题
『圆的方程』
圆的方程章节考查重点就在于中点的坐标和圆的标准方程以及圆的切线和弦的性质,该类题型相对来说较为复杂,这就要求在求解过程中考生能够准确地找出 Centre和对应的 Radius,其中对于直线与圆的位置关系可类比为一元二次方程根的个数问题,所以考生在入手该类题型时可考虑代入后形成一个新的一元二次方程的 Discriminant,再考虑其位置关系,再进行求解。很多考生在碰到该类题型时无法正确判断点所在位置以及相应线与圆的位置关系,还需引起重视。以 2021年 6月卷的第 6题为例:
 来源:2021年 6月卷 P2模块真题
来源:2021年 6月卷 P2模块真题
该类题型主要考查考生对于圆中切线性质的理解,大部分考生在解题时未理解关于 x轴切线时可运用数形结合的思想,即可通过画出该图像将圆心坐标对应的 y值与所求圆的半径相联系,从而求出 K值,然后再画出与 y轴的交点部分,即 x等于 0时所对应的 y值,进而求出面积,该类题型会更考查考生的动手画图能力,以下是理综部模拟作答情况,对于 (a)问利用数形结合思想并求出圆的半径从而求出 k值,但是对于 (b)问来说该考生并未解答,(b)问主要考查考生对于圆的理解以及作图能力,这需要考生能精准分析出圆的圆心坐标和半径以及圆与坐标轴的位置关系,从而通过图形对三角形的面积进行求解。
 来源:理综部模拟作答过程图
来源:理综部模拟作答过程图
『指数和对数』
指数和对数章节主要考查考生对于对数的理解,不少考生在对数的底数和真数上容易出现混淆,在求解过程中往往会因为分不清这两个概念导致计算错误。以 2020年 10月卷的第 9题为例进行,以下是理综部模拟作答情况。

来源:理综部模拟作答过程图
该考生解答 (i)问过程中对于对数的运算规则还是能够理解的,但对于把一个整数换成对数的过程还相对不够熟悉,导致运算错误而失分,非常可惜。(ii)问主要考查考生对于指数的理解,需要考生对指数的运算法则相当熟悉,该考生在指数方面的运用还不够熟练,不能够独立证明出该问的结论,理综教研部提醒考生通常可在题干中找出关键点“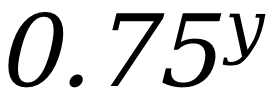 ”,即找到“
”,即找到“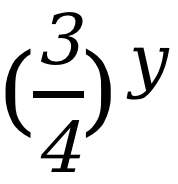 ”,然后凑出该表达式即可,步骤相较复杂,但难度适中。
”,然后凑出该表达式即可,步骤相较复杂,但难度适中。
 来源:2022年 10月卷 P2模块真题
来源:2022年 10月卷 P2模块真题