ALevel数学经典知识点！揭秘奇妙的“杨辉三角”与概率论背后的关系！

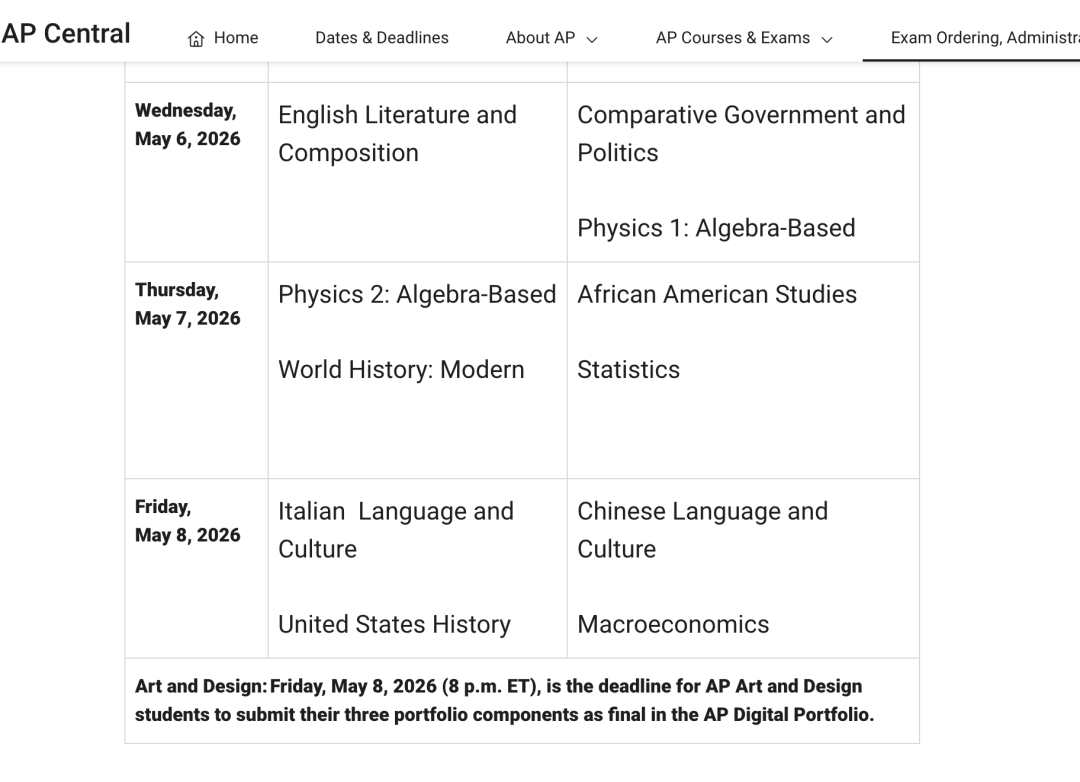
杨辉三角

早在北宋时期，我国数学家贾宪就发现了任意的高次方展开系数符合某种三角形的运算规律。200年后，南宋数学家杨辉在其著作《详解九章算术》中，详细解释了这种运算规律，并给出了一种数表，也叫做杨辉三角，300多年后，数学家帕斯卡也发现了该数表，并将其用于解决概率论的问题上，因此西方也叫帕斯卡三角。

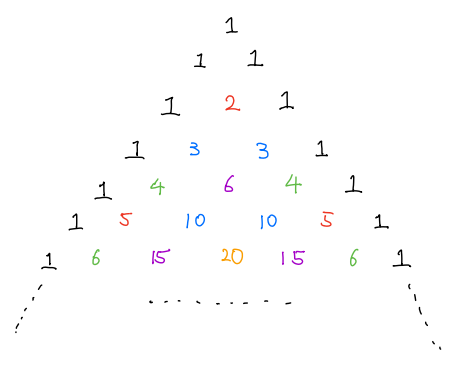
首先，我们来看看杨辉三角是如何得到的，我们根据上图，不难发现，杨辉三角内部的每一个数都等于它上面两个数的和，比如：

以此类推，我们可以得到完整的杨辉三角数表。

02、杨辉三角与概率论的关系

可是这个数表都有什么作用呢，它与概率论又有什么关系呢，下面我们来一一解释：

二项展开式：

众所周知，对于任意的a和b来说：

我们继续算更高次的展开式，我们还可以得到：

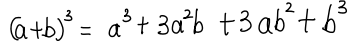
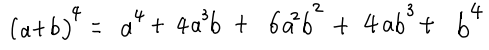
算到这里，我们发现，对于任意的一个a+b的i次方的二项展开式，它的系数都是杨辉三角中的第i+1行，但是如果想知道a+b的100次方展开式中的某一项的系数，显然用一个一个加的方式是不可行的。

所以，现在我们需要找到某种规律，可以找到杨辉三角中任意一行中的任意一个数，我们就可以对任意的二项式展开。

那我们回到开括号的算法上，a+b的i次方可以理解为i个a+b相乘：

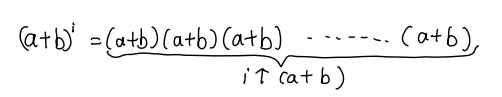
在相乘的时候，我们可以理解为每个括号里拿出一个a或者一个b，与其他括号拿出来的a或b乘在一起，比如：

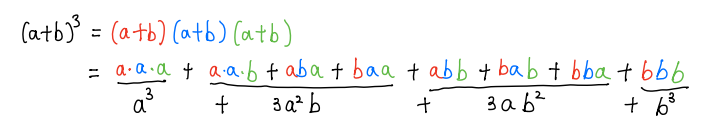
而这一过程就是一个随机的组合过程，在上面的例子中我们可以认为ab²的系数就是一个a和两个b在(a+b)³展开时有多少种组合形式，显然这种组合也可以认为在三个括号里随机挑选出一个a一共有多少种不同的方法，可以看到这个a可以来自第一个，第二个，或者第三个括号，一共3种不同的组合方式，因此ab²这一项前面的系数就是3。以此类推，我们可以得到(a+b)ⁱ的展开式中a^i-rb^r项的系数满足：

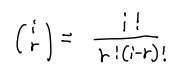
这样我们也可以对任意的(a+b)^I进行二项展开：

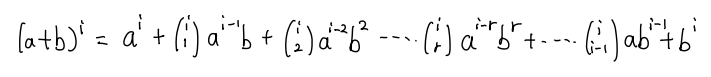
而其中每一项的系数都对应着杨辉三角的第i+1行的所有的数，这里我们会发现一个有趣的现象，如果a和b都等于1的话，我们发现杨辉三角第i行的和，都是2的i-1次方，就像这样：

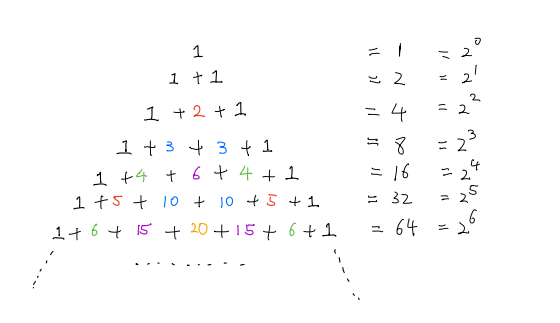
二项分布

杨辉三角同样也可以来研究概率论。如果我们抛一枚质地均匀硬币，很明显我们抛到正面和反面的概率各为1/2。但如果我们抛两次硬币，我们会得到三种可能的情况，两次正面，两次反面，或者一次正面一次反面，但是每种可能的概率是多少，我们可以得到如下的结论：

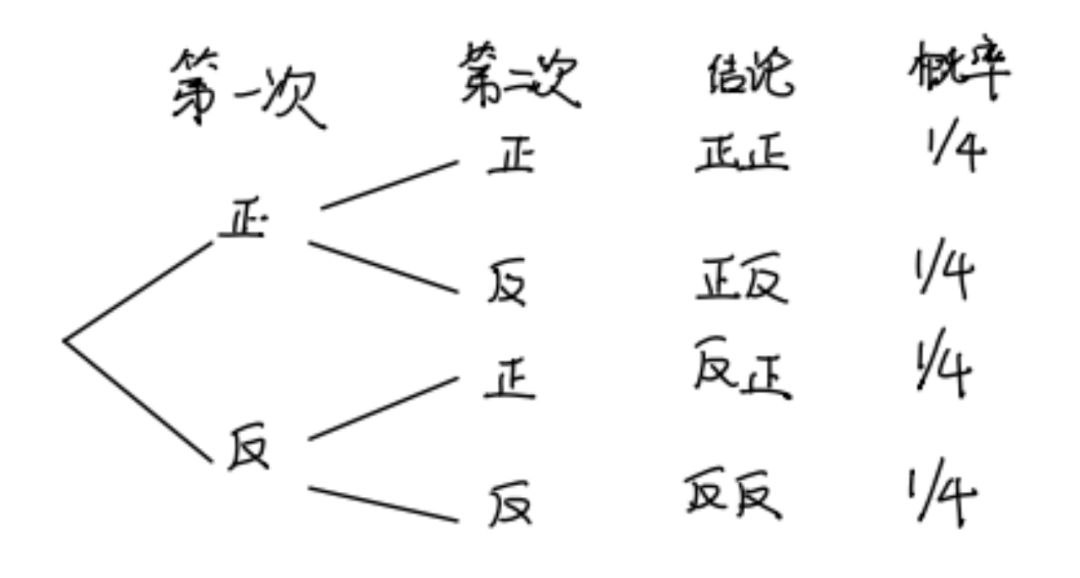
其中如果不考虑顺序的话，正反和反正都可以得到一次正一次反，因此得到一次正一次反的概率为1/2。如果抛三次硬币的话，我们还可以得到:

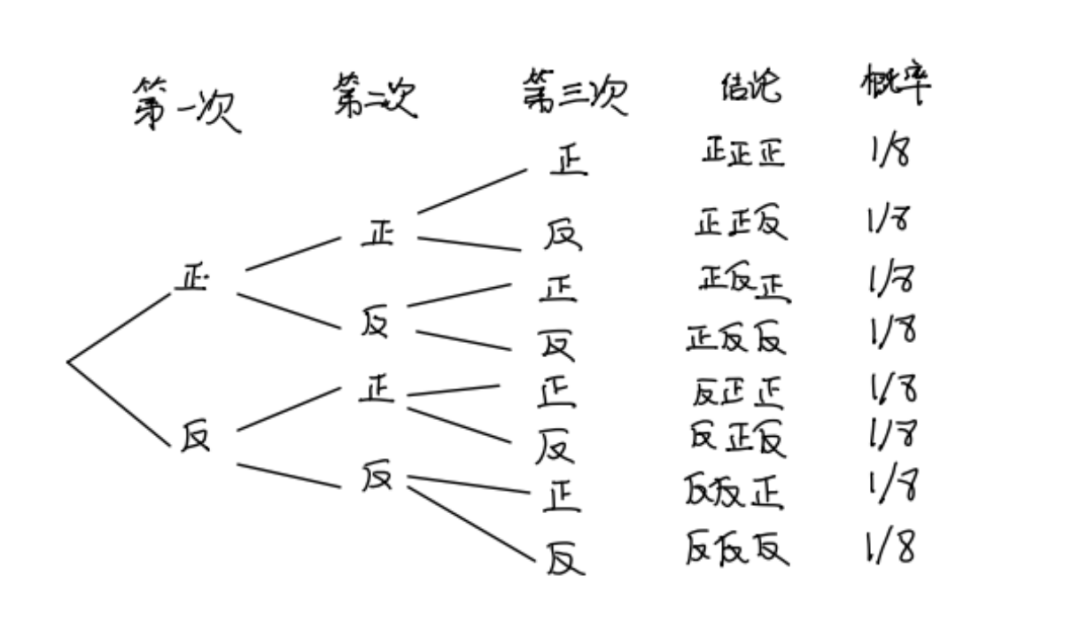
我们发现如果我们抛n次硬币，每次都有两种选择，如果其中有m次正面，(n-m)次反面，那我们一共有ⁿC_m种组合形式，而这个系数和(a+b)ⁿ展开式中a^mb^n-m的系数相同。而一共有2ⁿ种结果，因此抛出m次正面的概率可以表示为：

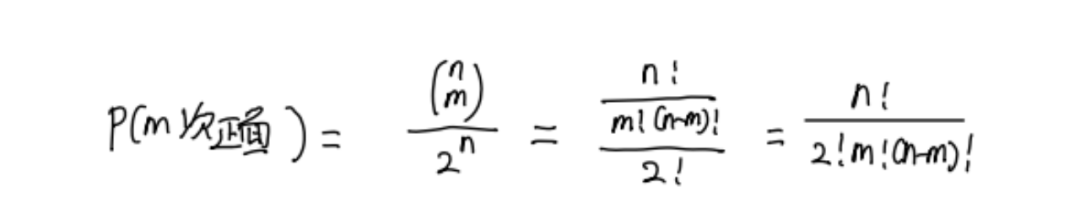
而这种概率的分布方式被称为二项分布。我们不难发现，除了抛硬币，我们生活中的很多只有两种选择的事情都符合二项分布。比如发生一件事的概率是p，不发生这件事情的概率就是1-p。如果我们还用抛硬币来理解，我们可以认为此时抛出正面的概率是p，抛出反面的概率是1-p。这时候我们抛n次硬币，其中抛出m次正面的概率就可以表示为：

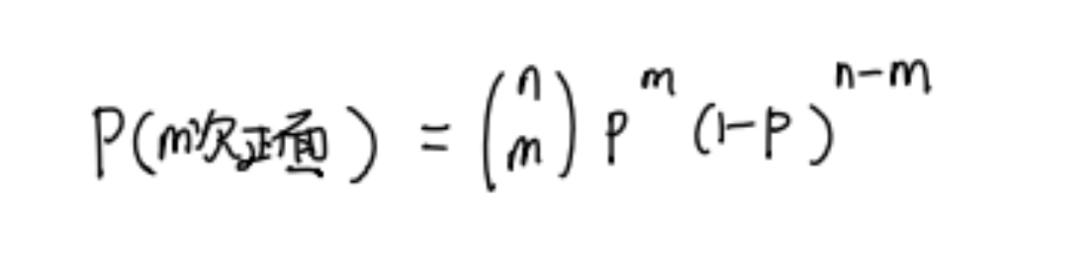
我们可以把这个概率理解为，二项展开式中a=p, b=1-p，的第m项。因为p一定是一个大于0小于1的数，所以我们不难发现如果n很大，我们很难一直抛硬币抛到正面，所以任何小概率事件，只要实验次数够多，就一定会发生，这也被人们称为“墨菲定律”。

除此之外，杨辉三角还蕴藏着很多其他有趣的数列和代数结构，如果我们把杨辉三角写成一个直角三角形，我们会发现，对角线上的数字可以构成一个斐波那契数列（任意一项的数字都等于前两项的和）：

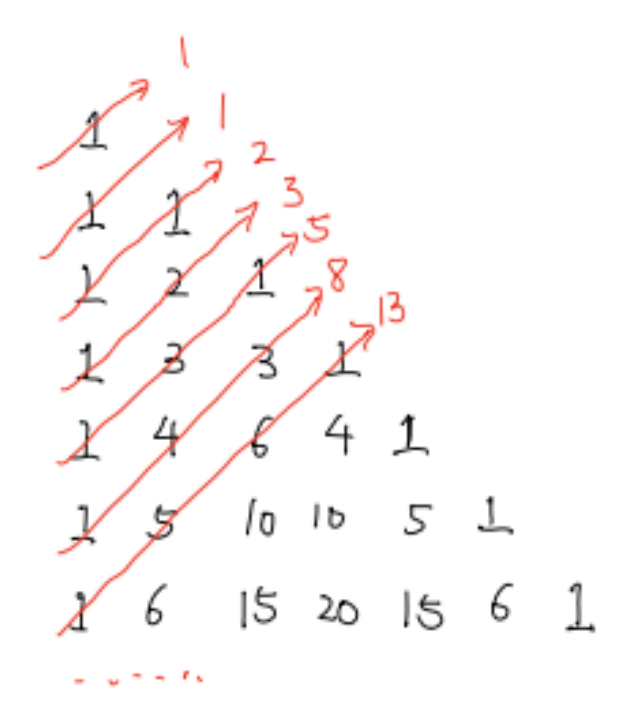
而杨辉三角的每一行还是11的幂：

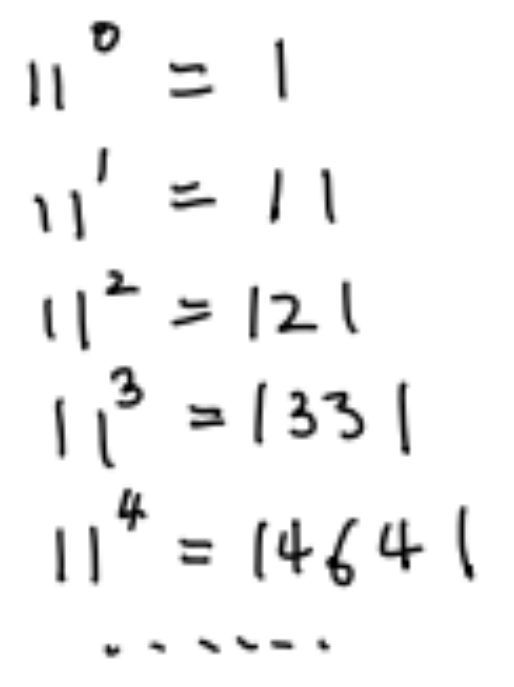
这里我们可以把11看成10+1，再用二项式展开我们就可以发现每一个二项式系数都对应这10的某个次方的系数：

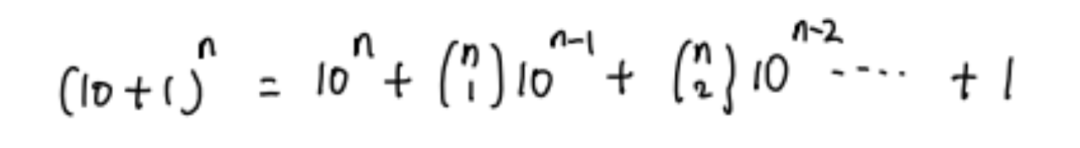
总结

所以看似简单的杨辉三角其实蕴藏着非常多的秘密，一定还有更多有趣的秘密隐藏其中，等着我们发现。