所有考AP物理1的同学注意！还有人不知道AP物理1考纲改革了嘛！
今天我们邀请到了机构AP数理老师，为大家分析更新后的“AP物理1的向量相关考纲内容”。
新考纲下，引入了更复杂的物理情境，要求学生能够在多维空间中处理更为复杂的运动问题。
张老师还为大家总结了大量示意图和例题，请大家一定要收藏转发！（家长朋友也要记得给孩子看哦！）
#01、物体在流动介质中的相对运动
在物体移动的过程中，当其所处的介质(例如空气、河流或风)也在流动时，物体的速度相对于静止观察者的速度将发生变化。这是相对运动的基本概念之一。
常见的例子包括：
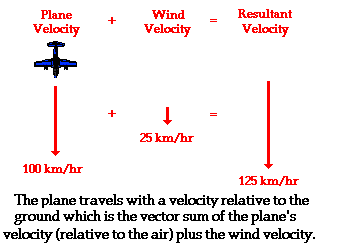
飞机在风中的运动：飞机遇到顺风(尾风)时，飞机相对于地面的速度将增大；遇到逆风(头风)时，飞机相对地面的速度将减小。
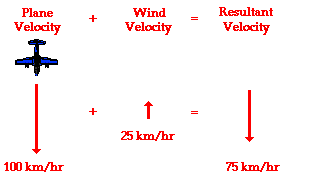
船只在河流中的运动：如果一艘船沿着河流行驶，即便船的速率恒定不变，水流的速度会影响船的最终运动轨迹和速度。
#02向量的加法与速度计算
当物体在流体中运动时，物体的速度相对于观察者的速度是通过矢量加法来计算的。以下是几个关键的计算步骤：
01、向量加法
顺风与逆风：如果物体与风的方向一致(顺风)，那么物体的相对速度将是两者的速度之和；如果方向相反(逆风)，则是两者的差。
侧风：如果物体和风的方向垂直，则需使用勾股定理来计算总速度。
02、例题与计算
Tailwind versus headwind problem: Suppose an aircraft is travelling at 100 km/h and encounters a wind of 25 km/h. If the wind is tailwind, the relative speed is 125 km/h; if it is headwind, it is 75 km/h. If the wind is a tailwind, the relative speed of the aircraft is 125 km/h; if it is a headwind, the relative speed of the aircraft is 75 km/h.
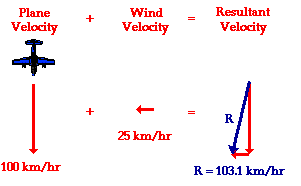
problem: If an aircraft is travelling in a southerly direction and encounters a westerly wind (speed 25 km/h), its final speed is the vector sum of the southerly speed and the westerly wind speed. This is obtained by the Pythagorean theorem:
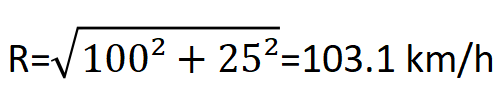
The direction can be obtained by calculating the inverse tangent function:
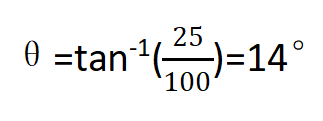#03河流中的运动分析
在河流中，类似于风的问题，水流也会影响船只的运动。
假设船只直接指向河的另一侧，但由于水流的影响，船只将不会直接抵达对岸，而是偏离。
此时，船的速度与水流的速度相结合，形成一个合成速度。
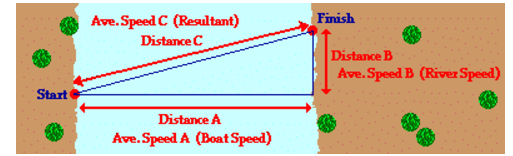
01、例题与计算
Suppose a boat is travelling with a velocity of 4 m/s,crossing a river in the forward direction, while the river is travelling with a velocity of 3 m/s, flowing laterally. By the Pythagorean theorem, the synthetic velocity is：
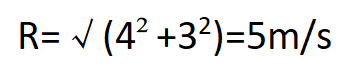
The direction is obtained by calculating the inverse tangent function：
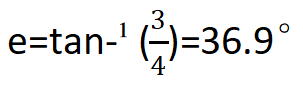
在物理学中，向量分量的独立性是一个至关重要的概念，尤其是在处理多维运动时。
这一概念的核心是：任何向量可以分解为互相垂直方向上的两个或多个分量，而这些分量之间是完全独立的。
一个方向上的分量变化不会对另一个方向的运动产生影响。
#04分量之间的独立性
水平方向与垂直方向的独立性：物体在一个方向的运动不会影响另一个方向的运动。
实例：
飞机遇到横风：假设一架飞机正朝北飞行，遇到来自西方的横风。风速增加会导致飞机的东向位移增加，但不会影响飞机的北向位移。
飞机的垂直（北向）速度仍然与风速无关，只会受到飞机引擎的影响。
气球下降：假设气球垂直下降的速度是 3 m/s，风速是 4 m/s 向东吹，气球在竖直方向上的运动是完全独立的，不受风速变化的影响。
即使风速增加到 6 m/s，气球的下降速度仍然为 3 m/s。
#05向量分量相互独立的原因
垂直方向和水平方向的分量之间没有直接的物理联系，它们是由不同的力或运动方式决定的，且作用于物体的方式不相互干扰。
简单来说，它们是互不影响的。
水平分量：例如，风速、地面速度等，这些分量仅影响物体在水平方向上的位移。
垂直分量：例如，重力、垂直速度等，这些分量仅影响物体在垂直方向上的位移。
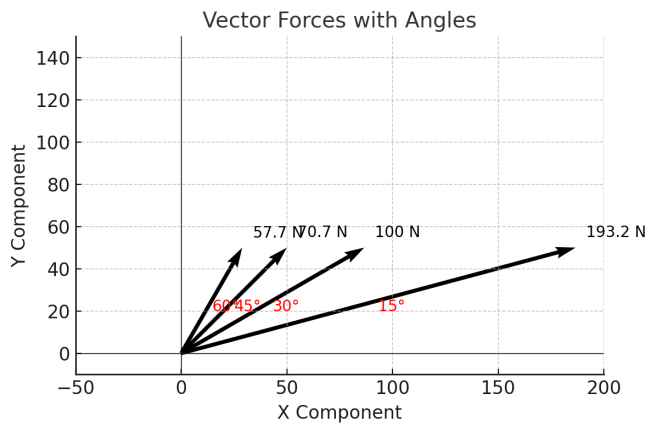
#06实际应用：物体的轨迹与分量
在处理运动轨迹时，水平和垂直方向上的分量将分别决定物体的水平方向位移和垂直方向位移。
水平和垂直分量的独立性使得我们可以分别计算两者的运动时间和位移，从而得到最终的结果。
投射物的运动：投射物在水平方向和垂直方向的分量是完全独立的。
水平方向的速度由发射速度和角度决定，垂直方向的速度则由重力和发射速度的垂直分量决定。
水平方向的位移和垂直方向的下落是两个独立的运动，最终投射物的轨迹是由两者合成的。
是不是感觉到豁然开朗？
【竞赛报名/项目咨询+微信：mollywei007】
