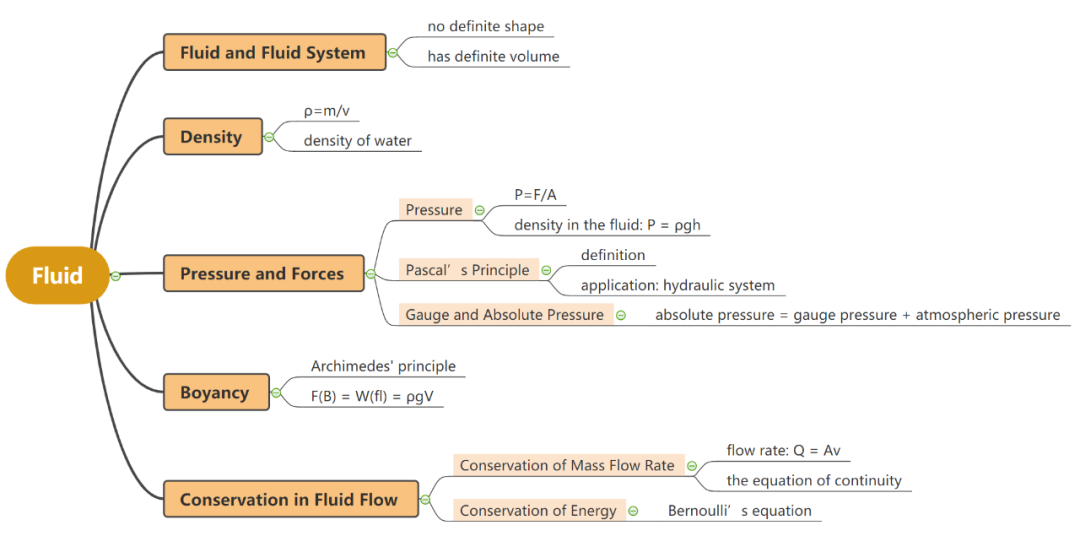
本文目录
1、Fluid and Fluid Systems
2、Density
3、Pressure and Forces
3.1 Intro to Pressure
3.2 Pressure in a Fluid3.3 Pascal’s Principle
3.4 Gauge and Absolute Pressure
4、Buoyancy
5、Conservation in Fluid Flow
5.1 Conservation of Mass Flow Rate
5.2 Conservation of Energy
NO.1、Fluid and Fluid Systems
我们知道，世界上各种各样的物体各自以不同的形态存在着，但大致可以被分为三种形态：固体(solid)，液体(liquid)，气体(gas)。这三种形态看起来就有很大的不同：
| 三种形态对比 | |||
|---|---|---|---|
| Solid | Liquid | Gas | |
| 确定的形状 | √ | × 形状会随着容纳它们的容器而变化 | × |
| 特定的体积 | √ | √ | × 分子会扩散去填满容纳它们的容器 |
为什么三种形态会呈现出如此不同的特征呢？这其实与构成物体的原子（atoms）之间的互动方式有关。 固体中的原子们关系非常好，喜欢紧紧与彼此贴在一起，它们之间的力允许原子产生一些振动，但很难改变原子之间的相对位置。
如果我突然给屏幕前的你来一拳，你也不会瞬间瓦解、失去人形，因为组成你身体的原子不能自由自在地移动（被锤得鼻青脸肿、五官稍微有点变形的那种变形不算！）
和固体不一样，液体在受到外力时很容易变形，因为液体里的原子可以自由地四处移动并改变相邻原子的位置——俗称“流动”。不过液体还保持着比较固定的体积，因为原子构成的分子会通过相互吸引聚集在一起。 气体里的原子大概是最幸福的了，因为它们可以受极少束缚、随心所欲地到处移动，像液体那样流动自然是不在话下。
因为液体和气体都可以流动，所以它俩被一起称作流体(fluid)。但因为气体里的原子之间的距离间隔非常大，它们之间的作用力很微弱，所以连体积也不怎么固定。 在这里，我们要引入“系统(system)”的概念。
一个系统是由更小的结构组成的，而系统的性质是由组成它的原子和分子结构的（1）性质和（2）这些粒子之间的相互作用决定的。在AP物理中，当组成部分的属性对宏观系统的行为建模不重要时，系统本身可以被看作一个对象。
也就是说，当我们在讨论一杯水的时候，不用把它拆成一个个水分子或者氢原子氧原子，而把这一杯水当成一个整体（也就是一个对象）来分析就好了。
NO.2、Density
一斤的铁和一斤的棉花，哪个更重呢？
这个古老的谜题向我们展示了质量(mass)和密度(density)之间的区别。一斤当然就是一斤；但是因为铁的密度比棉花大得多，所以我们从直觉上倾向于认为铁更重。 密度是物质的重要特征之一。
比如，我们可以通过物体的密度来确定它是在流体中下沉还是浮起来（比如你会不会在自己的泪水池里淹死）。密度指的是物体单位体积的质量，国际单位是kg/m3，表示为： 记住最常见的流体之一——水的密度（在4℃的环境下）为1000 kg/m3。
NO.3、Pressure and Forces
3.1 Intro to Pressure
你一定听说过高血压（尤其是老师或者父母很生气的时候）、低血压，也听说过高气压、低气压，而这些“压”实际上指的是流体（液体或者气体）所带来的压强(pressure)。 压强的定义是：力除以垂直于所施加的力的面积，表示为：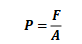
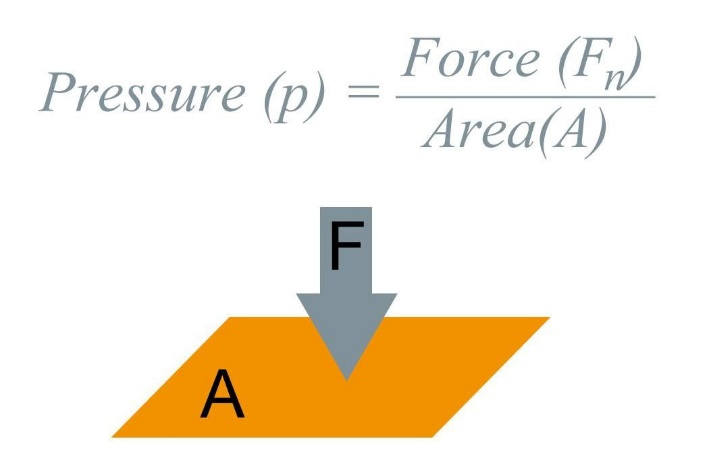
图1
压强的国际单位是帕斯卡(pascal/Pa)，并且从压强的计算公式很容易可以得知：1 Pa = 1 N/m2。 取决于力所施加的平面的面积大小，一个给定的力可以对一个平面产生很不同的影响：同样重的砝码会对施加平面产生一样大的压力，与施加平面的接触面积越大，对其产生的压强就越小；接触面积越小，对其产生的压强也就越大（如图2所示）。
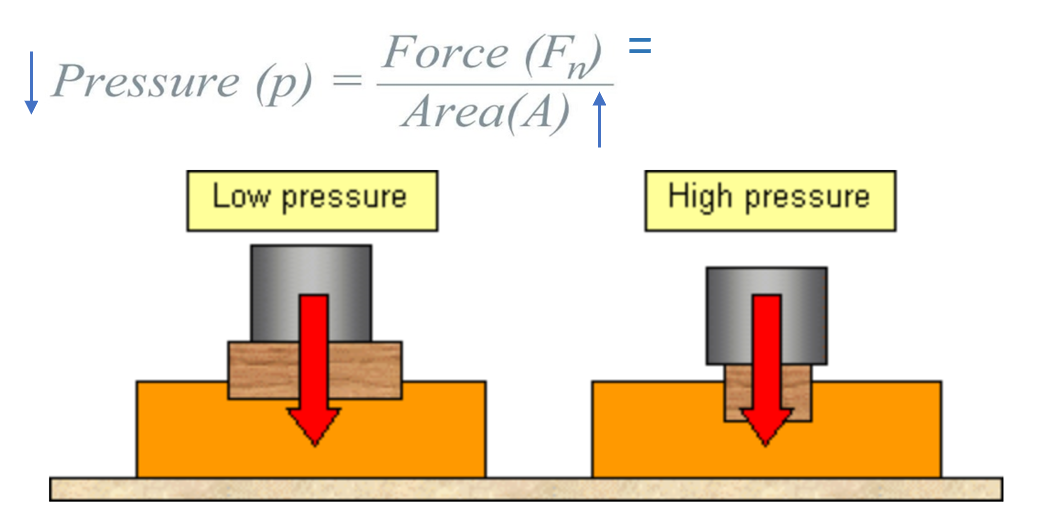
图2
这个产生压强的力有哪些特点呢？
首先它有明确的方向——总是垂直于力所施加的表面。其次，压力会把压强施加在它所接触的整个表面上。比如，在池子里游泳的人能感受到来自四面八方的水所施加的压强。
3.2 Pressure in a Fluid
如果你曾经在海里游过泳，并且有潜在水底下的话，你一定感受到过那种流体带来的压强。而且位置越深，这种压强会越大。 这种水底下的压强怎么计算呢？比如图3中容器底部受到的流体压强？
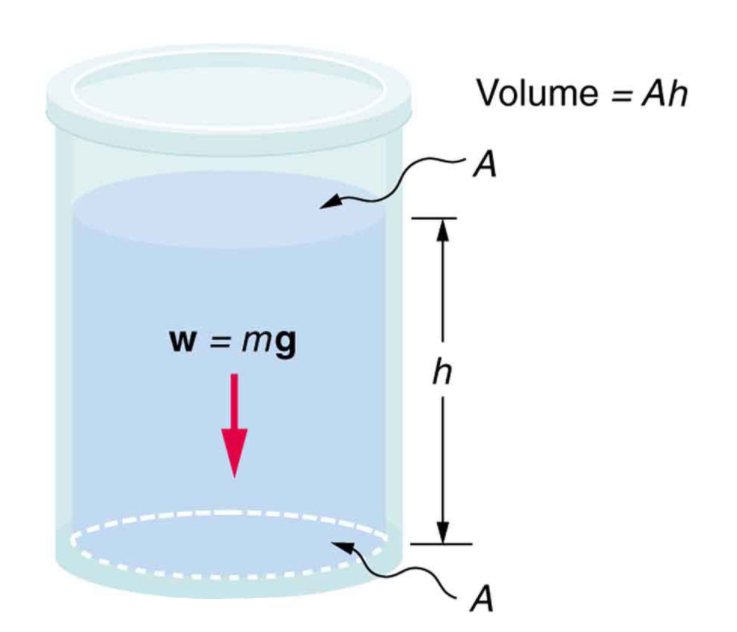
图3 首先容器底部受到的力来自于液体的重力w = mg，那么它所受到的压强就是P = F/A = W/A = mg/A
这样我们就得到计算液体底部的压强公式啦！ 什么？你说如果想知道液体其他位置的压强怎么办？ 那把h改一改，改成那个位置的高度就可以了嘛。因为你可以把那个位置所在的横截面看作新的底部，这个横截面所受到的压力等于压在它上面的液体的重力，那么公式的推导过程就和上面写的一模一样啦！
【真题速递】
（2016 Q18）
解析：
这其实是在变相地问我们处在哪个深度的水可以产生最大的压强，因为对于同样大小的出水孔(A)，压强(P)越大意味着压力(F)越大，越大的压力产生越大的加速度(a)，导致水在出管时越大的的初始水平速度和越长的水平运动距离。
对于液体来说，深度越大压强越大，所以P(C) > P(B) > P(A)，根据上述一连串的推导过程，得到dc > db > da，选择D！
3.3 Pascal’s Principle
当一个压强被施加在封闭流体里，会发生什么呢？ 因为流体中的原子可以自由自在地移动，所以它们在受到压强后，会将压强传递到流体的各个部分和容器壁上（毕竟它们可以相互碰撞）。而且在传递的过程中，压强的大小会保持不变。这个现象最初被Blaise Pascal这位法国科学家描述，所以被称为Pascal’s Principle（帕斯卡原理）：
A change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
关于Pascal’s Principle最重要的应用之一是hydraulic system（液压系统）——这是一个用来施加力的封闭流体系统。最常见的液压系统大概是控制汽车刹车的系统。一个简单的液压系统如图4所示。
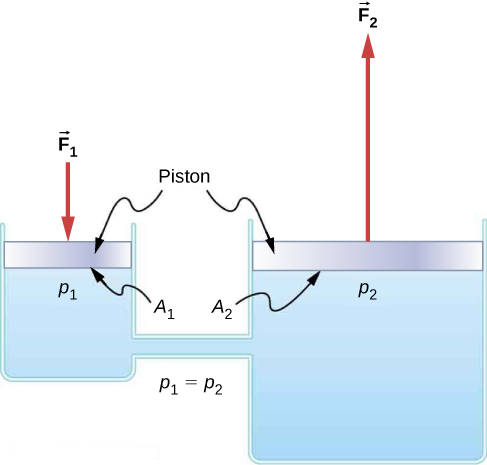
图4 我们可以通过Pascal’s Principle来推导出一个简单液压系统的力之间的关系。首先要注意的是，系统中的两个活塞高度相同，因此不会因为深度不同而产生压力差异。 因为压强可以由P = F * A算出来，所以 F1作用于区域A1上的压强P1=F1*A1。
根据Pascal’s Principle，这个压强可以在液体中被完美传递到各处，包括另一个活塞那里。因此，另一个活塞受到的压强P2等于P1。又因为P2=F2 * A2，所以我们可以得到关系式：F1 * A1 = F2 * A2。 简单来说就是：
P1 = P2 //Pascal’s Principle
F1 * A1 = F2 * A2
别忘了，这个关系成立的前提条件是：
1）活塞处于相同的竖直高度；
2）系统中的摩擦力可以忽略不计。
有了这个关系式，液压系统就可以帮助我们在一个地方去增加或减少施加在另一个地方上的力啦！比如，如果我们的控制端在A1，并且已经尽可能施加了最大的力F1，那么为了增加施加在另一端的力F2，就要使另一端的受力面积A2尽可能的小。
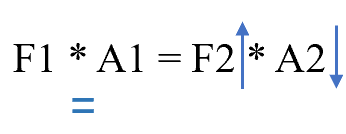
3.4 Gauge and Absolute Pressure
在你坐着父母的车去上学的路上，突然你感到一阵颠簸，紧接着车子便熄火停了下来——糟糕，轮胎漏气了！压胎表上显示的数字逐渐趋近于0。
但轮胎里真的就没有一点压强了吗？ 不，外界的大气压还在给轮胎施加着压强。那为什么压胎表上会显示0呢？因为压胎表就是这么设计的：当轮胎气压等于大气压的时候显示0，当轮胎气压大于大气压的时候读数为正——两者的差值。
类似压胎表这样的压强测量工具（比如血压表）常常会忽略大气压强，因为它几乎无处不在，所以当轮胎只受大气压强作用的时候压胎表会显示0。我们把压胎表所显示的相对于大气压强的压强称为gauge pressure（表压）：当实际压强>大气压强，表压为正；当实际压强＜大气压强，表压为负; 当实际压强=大气压强，表压为0。
这个实际压强也就是总压强，被称作absolute pressure（绝对压强）。绝对压强、表压、和大气压强之间的关系是：absolute pressure = gauge pressure + atmospheric pressure
NO.4、Buoyancy
回到文章标题所提出的问题——我们在泪流成河（字面意义）里大概率不会淹死，是因为我们在水里可以受到一个水向我们施加的向上的浮力。
浮力到底是何方神圣？
浮力现象的产生基于这样一个事实——流体中的压强随深度的增加而增加。这意味着：流体中物体底部受到的向上的力大于物体顶部受到的向下的力，这个压力差（F2-F1）也就是物体所受到的浮力（见图5）。
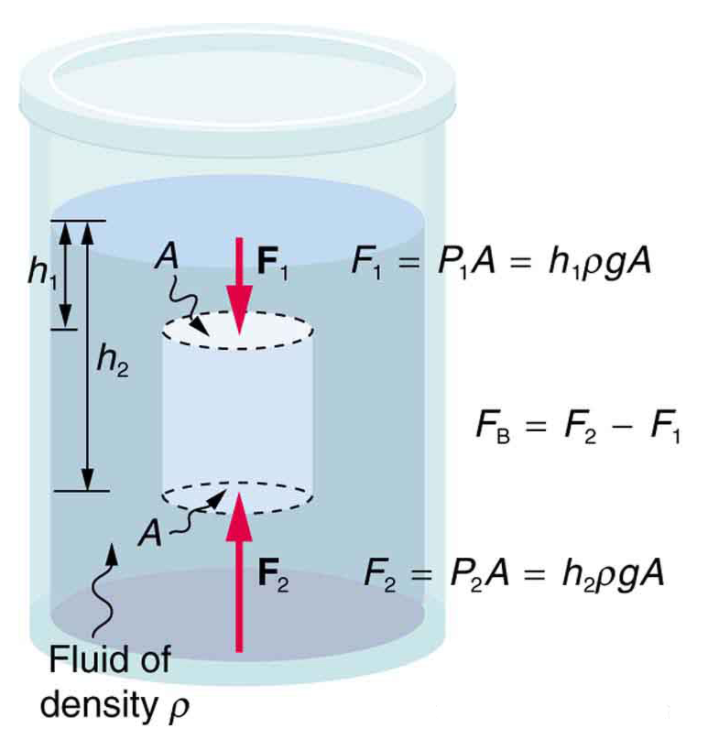
图5
流体中的物体受到两个力：向上的浮力和向下的重力。当浮力大于物体重力时，物体会上升直到浮在水面上；如果浮力小于重力，物体会下沉；如果凑巧两个力相等，物体就会悬浮在流体中静止不动。 浮力要怎么计算呢？让我们先来想想看当一个浸没在流体里的物体被取出的时候发生了什么。
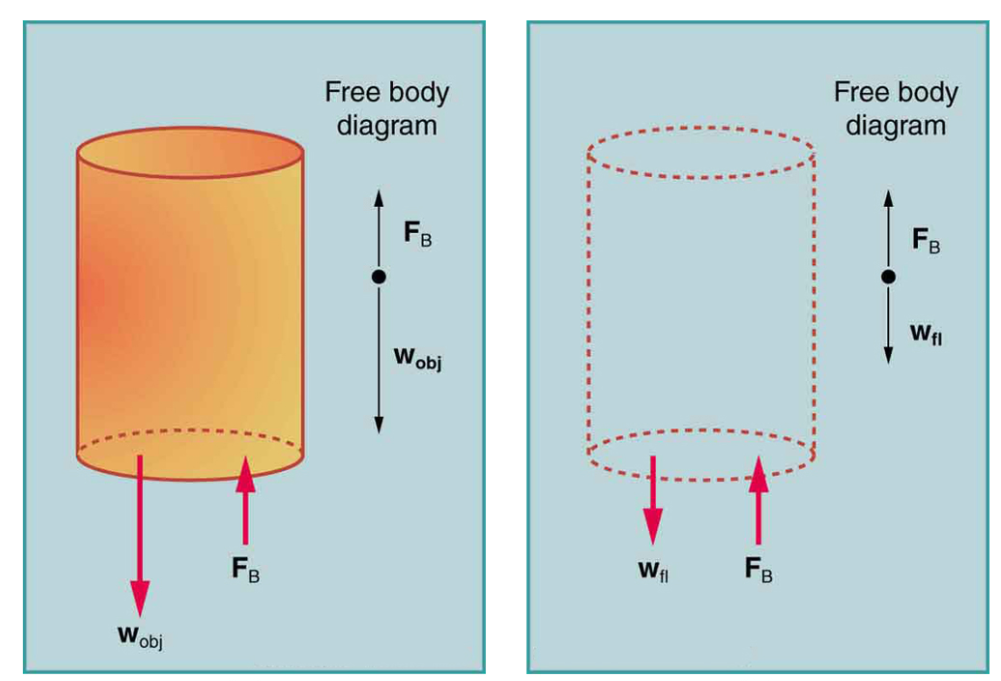
图6
从图6中我们可以看到，这个物体原本所占的空间会被重量为Wfl的流体所填充。因为这“块”流体（被虚线框起来的）需要被底下的流体支撑，以静止在原处，因此这块流体所受到的浮力FB应该等于Wfl，也就是被物体排开的这块流体的重量。
这一关系最早是由Archimedes（阿基米德）提出的，因此它被称作Archimedes’ principle（阿基米德定律）：物体所受的浮力等于它所排开的流体的重量，即FB = Wfl 再拓展一下公式，我们可以得到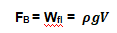
其中指的是流体密度，V指的是物体浸没在流体中的体积 = 物体所排开的流体体积。 密度在Archimedes’ principle中起着至关重要的作用——一个物体的平均密度最终决定了它是漂浮还是下沉。如果它的平均密度小于周围流体的密度，它就会漂浮。为什么呢？
这是因为如果流体具有更高的密度，也就意味着被物体所排开的流体具有更多的质量（别忘了物体浸没在流体中的体积 = 物体所排开的流体体积）和更大的重力。而根据Archimedes’ principle，浮力FB等于排开的流体的重量Wfl。Wfl大于物体的重力，也就意味着浮力FB大于物体的重力，物体自然也就上浮啦！ 那么同理，我们也可以推断出：比流体密度大的物体会下沉。
【真题速递】
（2016 FRQ Q2）
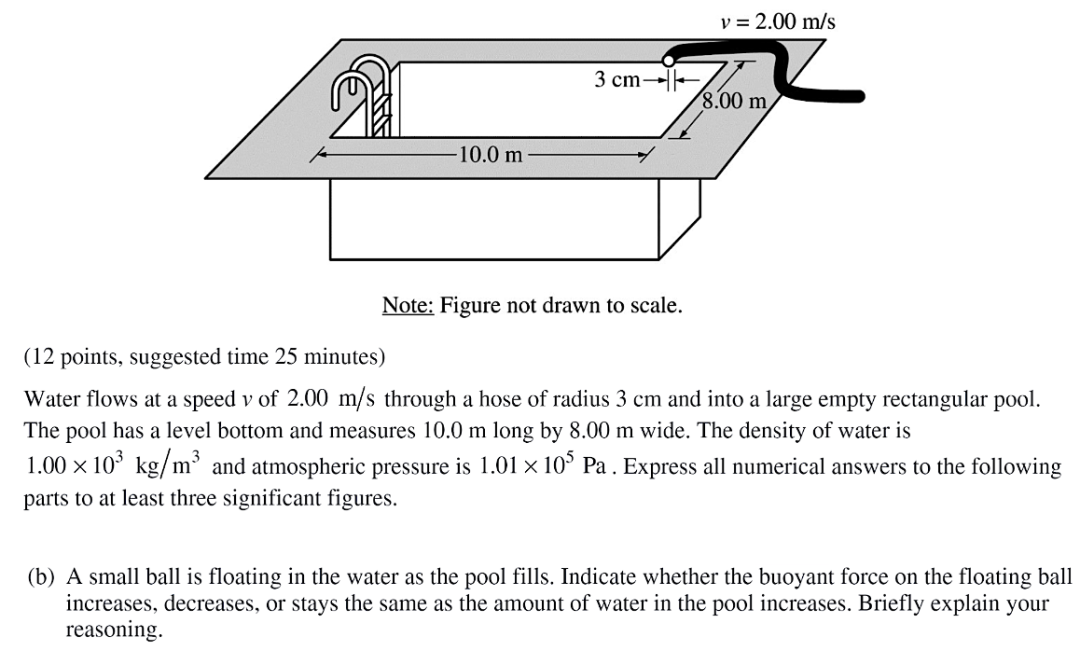
刚开始小球就浮在水面上，说明小球的密度比水小，无论池子里装了多少水都无法改变这个事实，因此小球会一直浮在水面上。因为浮力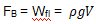
，水的密度ρ不变，小球没在水面以下的体积V不变，说明小球受到的浮力也不会变。 参考回答：The buoyant force on the ball depends only on the amount of water displaced by the ball which does not change as long as the ball is floating.
NO.5Conservation in Fluid Flow
到目前为止，我们探讨的流体都是处于静止状态的。但我们知道，流体既然叫“流”体，就说明它们是可以流动的。接下来我们就将一起学习处于动态中的流体具有哪些性质和特点。
5.1 Conservation of Mass Flow Rate
流体的flow rate（流速）Q指的是一段时间内流经某一区域某一位置的流体体积（见图7），表示为：Q = V / t 因为体积（V）可以被表示为底面积（A）*高度（d），所以我们把公式变一变，又可以得到：Q = Ad / t d/t，一段长度除以时间是什么呢，那不就是速度嘛！所以：Q = Av 把体积V和速度v看清楚啦，别弄混了！
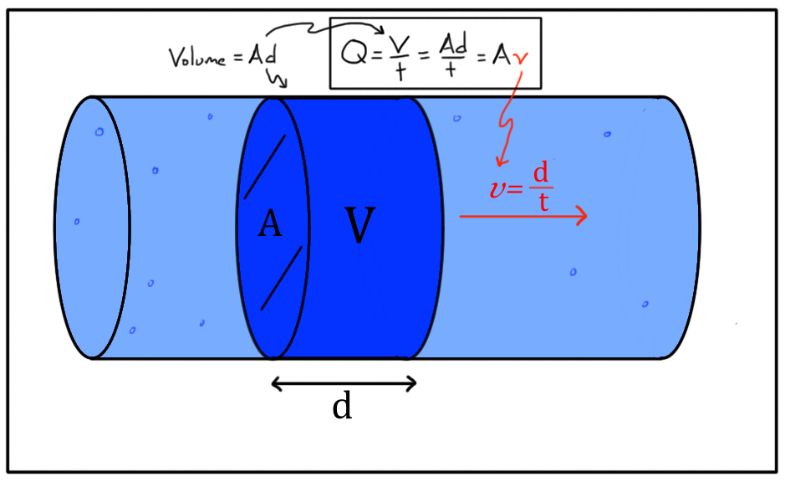
图7
从公式中我们可以看出，flow rate（流速）和velocity（速度）的联系很紧密，但它们的不同点在于：flow rate是单位时间内流过某个位置的液体体积，而velocity在这里指的是线性的速度，也就是单位时间内液体流过的距离。
想想一条河流的flow rate：河流的velocity越大，河流的flow rate就越大。但是flow rate也取决于河流的宽度或者横截面——一条小溪流即使很湍急，它单位时间内流过的体积（即flow rate）还是要比大河少得多。 然而，一条河流不可能处处都一样宽，这意味着河流在流动的过程中，横截面积A将产生变化。
图8
图8中的管道为河流宽度的变化提供了一个简单的模拟。我们可以看到，水在沿着半径递减的管道流动。由于流体是不可压缩的，在给定的时间内，必须有等量的流体流过管道中的任何一点，以确保流动的连续性。
也就是说，对于没有被压缩的流体来说，在它流动的过程中的任何时候都有着相等的flow rate——这被称作the equation of continuity。 在这种情况下，由于管道的截面积A减小，速度v必然增大，因为
Q1 = Q2A1 * v1 = A2 * v2
A2 < A1v2 > v1
5.2 Conservation of Energy
The equation of continuity告诉我们，当流体流入较窄的通道时，它的速度会增加——这意味着它的动能也增加了。但推动动能变化的源头到底是啥？ 变化的动能其实来自：将流体推入通道所做的净功+重力对流体所做的功（如果流体的竖直位置有变化）。
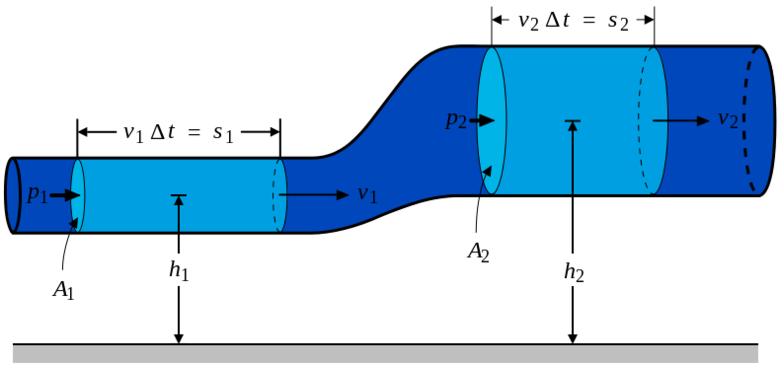
图9
那么在流体流动中的任意一点，它的总能量将等于三个能量之和：一个将流体推入通道所做的净功+动能+重力势能。根据能量守恒定律，在流体这个系统中，如果忽略阻力并且没有来自系统以外的外力（表现为流体没有被压缩），流体的总能量应该是不变的。这意味着：
Wnet + Wkinetic+WG = constantFd + (1/2)mv2 + mgh = constant(PA)d + (1/2)mv2 + mgh = constantP(Ad) + (1/2)mv2 + mgh = constantPV + (1/2)mv2 + mgh = constant
各项除以体积V：PV/V + (1/2)(m/V)v2 + (m/V)gh = constant 最后我们将得到：P + (1/2)v2 + gh = constant 这就是由能量守恒推导出来的Bernoulli’s equation，在任何没有被压缩以及忽略阻力的流体系统中成立。因为流体的总能量恒等于一个常数，所以如果我们任意取两点（见图9），总可以得到：
P1 + (1/2)v12 + gh1 =
P2 + (1/2)v22 + gh2
【真题速递】
（2017 Q134）
解析：
题目中 “ideal fluid”的表述向我们暗示了这个流体系统能量守恒，可以应用Bernoulli’s equation：P + (1/2)v2 + gh = constant。我们需要判断流体pressure的变化，就得判断流体速度的变化和重力势能的变化：根据the equation of continuity，不可压缩的流体flow rate会保持不变，Q = A* v = constant，因为管口变窄，所以速度v会增大；因为管道高度增加，所以重力势能也会增大。在(1/2)v2 和gh都增大的情况下，P应该变小。 所以选择A和C！
结 语
关于流体的知识你掌握了吗？收下这份思维导图，助你AP55555！
【竞赛报名/项目咨询+微信：mollywei007】
