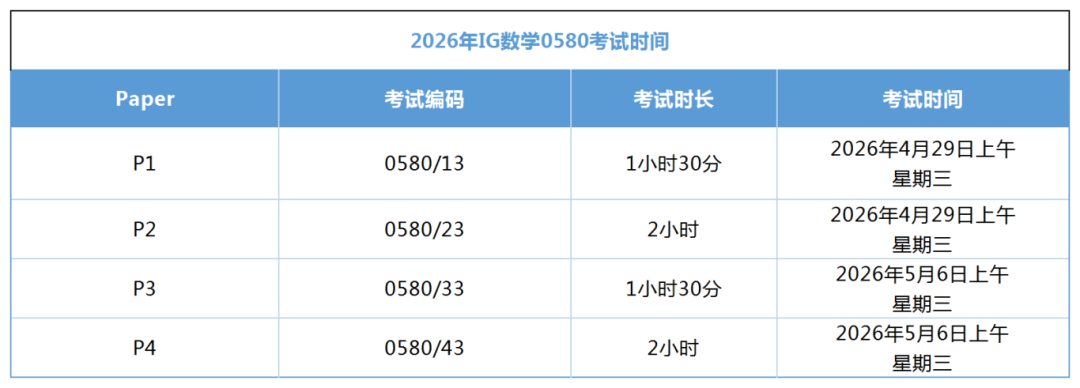
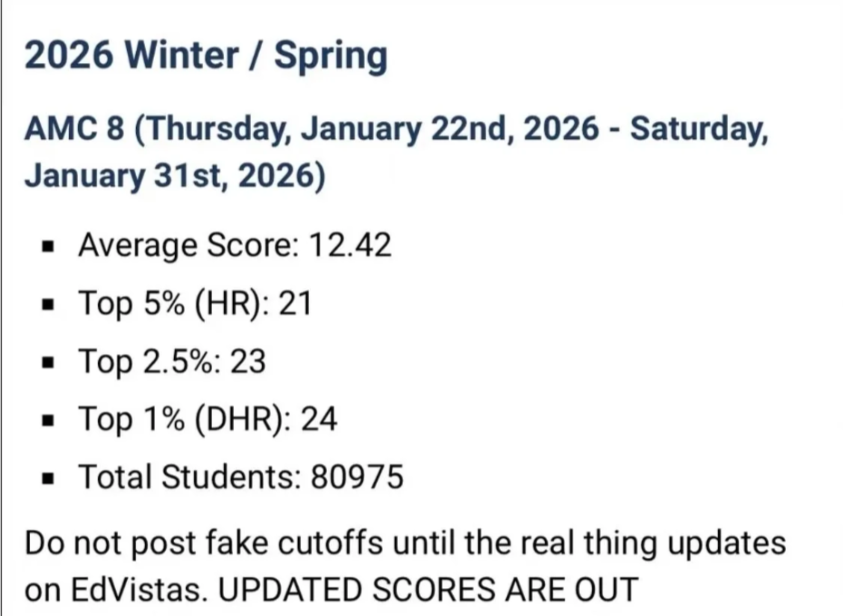
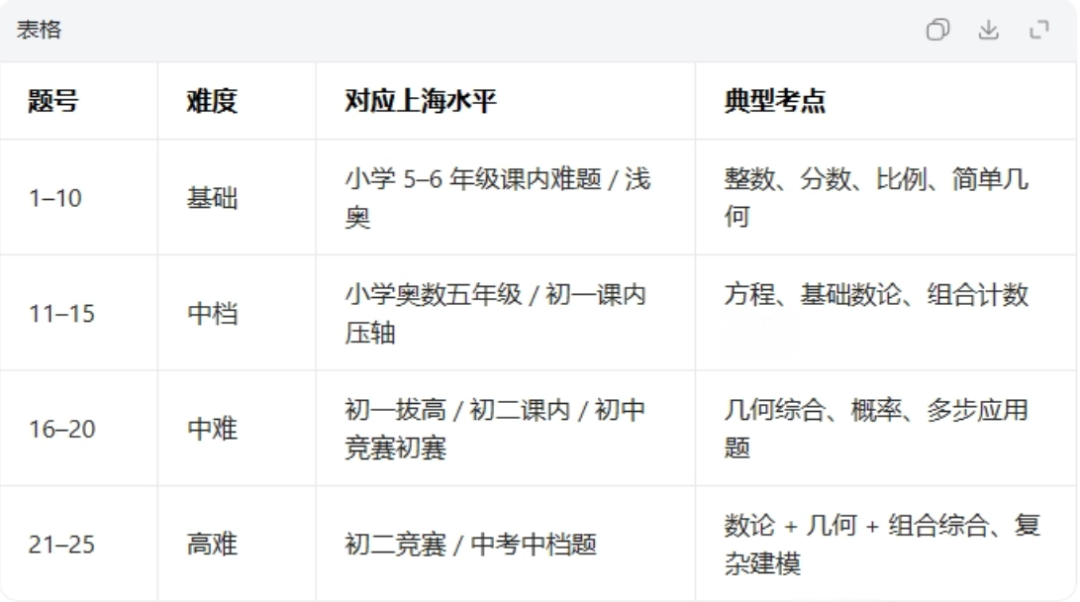
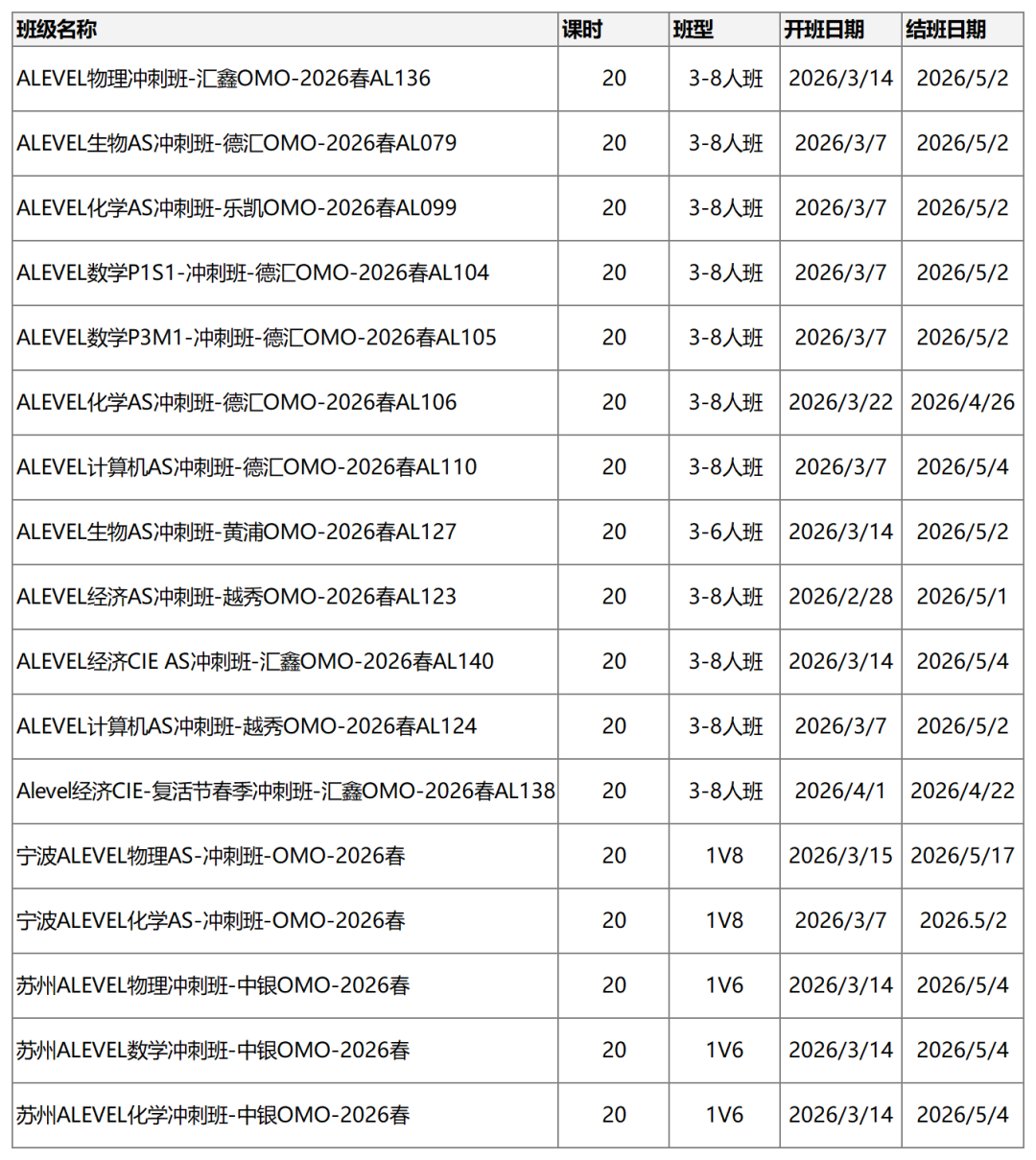
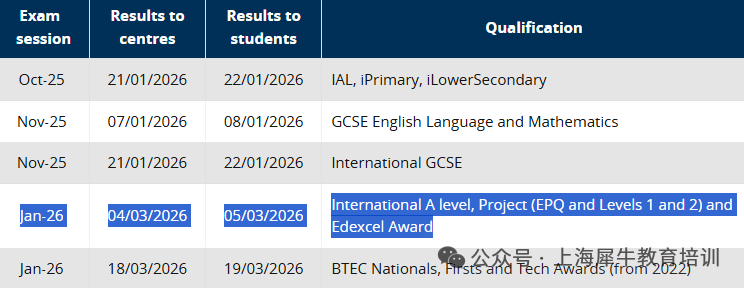
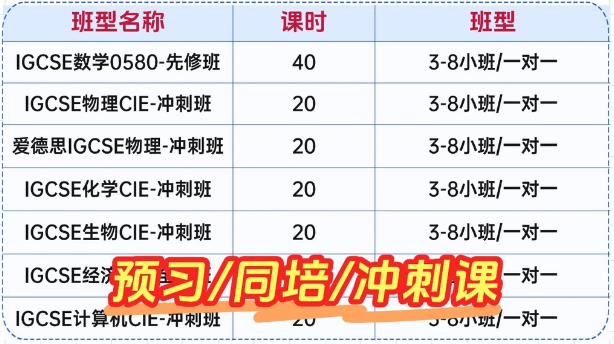
现在已经进入三月份，距离5月4号的考试还有2个月的时间，大家如何保证在复习过程中不要跑偏，确定要复习哪些重点知识点呢？ 这篇文章里，一丁老师为少年和小仙女们，梳理了在AP统计学考试中基本年年必考的考点，大家在复习过程中，一定要重点掌握，弄懂弄通。
Unit 1 Exploring Categorical Variable
1. 明确展示单变量分类变量的图形有bar chart、pie chart，展示双变量分类变量的图形有：side-by-side bar chart和segmental bar chart，容易出选择题。
2. 掌握单变量分类变量的假设检验（chi-square test of goodness of fit）四步骤，选择题、简答题都有出题的可能。要熟练掌握计算器的操作，以及利用chi-square cdf来找到pvalue。
3. 
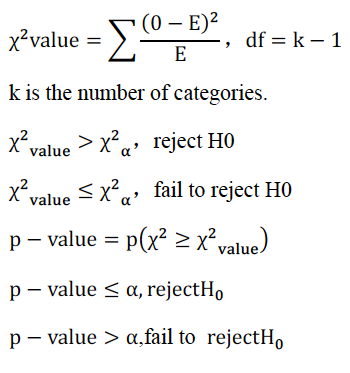
4. 掌握双变量分类变量数据的展示表格—two way table（必考）。
（1）结合概率（probability）考查
例（2010年Form B） 
参考答案 
（2）掌握通过side by side bar chart，segmental bar chart如何描述变量之间的关系（简答题易考）。 特别注意画图一定要基于条件概率（conditional probability）的基础上。 例（2009年Form A）
参考答案 
（3）掌握卡方独立性检验（chi squre test of independence）以及卡方比例同质性检验（chi-square test for homogeneityof proportions），特别是在碰到简答题时一定要区分好是哪种检验。
Unit 2 Exploring Numerical Variable
1. 对于单变量数值型数据（univariate numerical data）
（1） 掌握频数分布表，累积频数分布表，看图时一定看好y轴坐标轴用的是frequency 还是percent等。
（2）掌握展示图形（4种）：点图（dotplot）、茎叶图（stem-and-leaf plot）【茎叶图易考简答题】注意；茎叶图的规则是末位数字是leaf，其它部分是stem，要注意在画图过程中对数据进行说明，比如73，要写上7|3代表73。 —直方图（histogram） —boxplot（箱线图）--每年必考。 特别注意：boxplot无法看出数据个数的多少，以及boxplot中线的长度大小不代表数据个数的多少，二者没有对应关系。
（3）掌握判断outlier的标准： 
（4）每年必考：describe或者compare distributions（结合4钟图形）如果考到简答题，一定要涉及四方面：shape、center、spread以及其他usual features（如是否有outlier、gap and cluster） 例（2010年FormB）
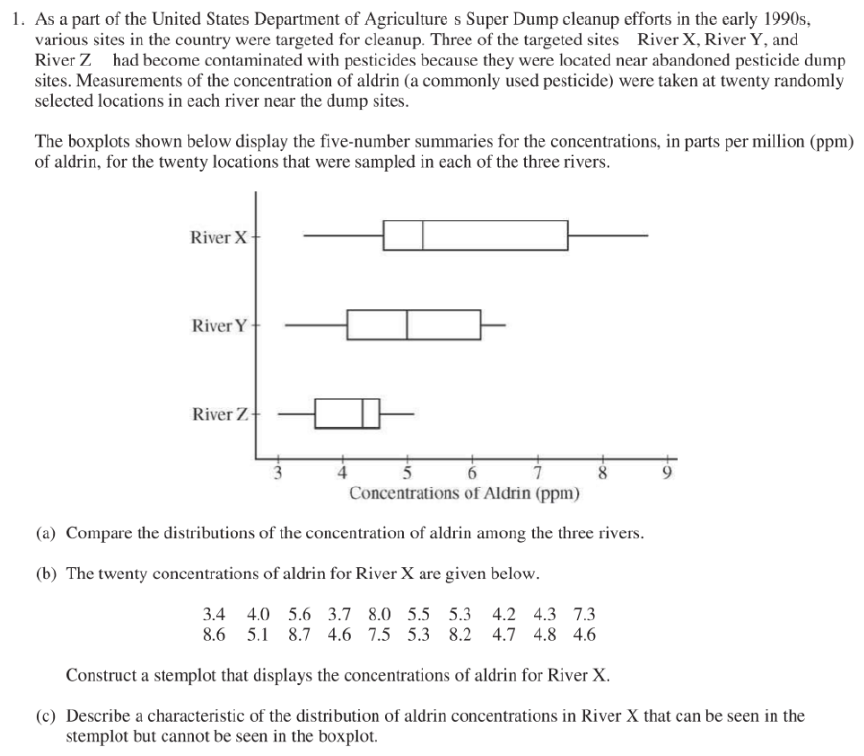参考答案： 
2.对于双变量数值型数据（bivariate numerical data） 简答题中大概率会有最小二乘回归线的题目。
（1）掌握展示图形—散点图（scatterplot）并能结合题目的背景信息通过散点图描述两个变量之间的关系特征。 主要从四方面展开：形式（form），方向（direction），强度（strength）以及其他unusual features。该考点非常高频考，需要特别注意：association≠causation。所以在简答题中出现时千万不要用cause之类的词，可以用tend to。特别注意结合y=x这条直线。 例（2015年）
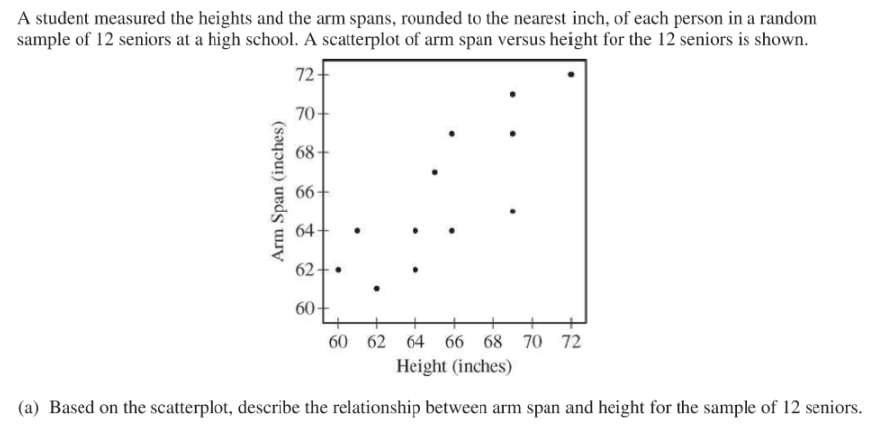参考答案： 
（2）掌握相关系数（correlation）r的概念，明确-1≤r≤1，明确改变变量计量单位、对变量上的每个数字加减常数或乘一个大于0的常数，r都不变，易考选择题。
（3）
（4）掌握如何计算残差（residual）并解释其含义。
（5）
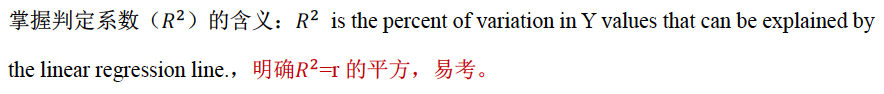
（6）残差图（residual plot）以及什么样的残差图代表模型拟合好（residuals around 0 and the residual plot shows no pattern），该考点易考。
（7）掌握异常值（outlier），高杠杆点（high-leverage point）以及有影响的点（influential point）。An outlier is a point that does not follow the general trend shown in the rest of data. A high-leverage point has a substantially larger or smaller x-value than the other observations have. An influential point is any point, if removed, changes the relationship substantially(for example:slope /y-intercept/ correlation)
（8）线性回归模型要掌握如何读取statistical outputs。
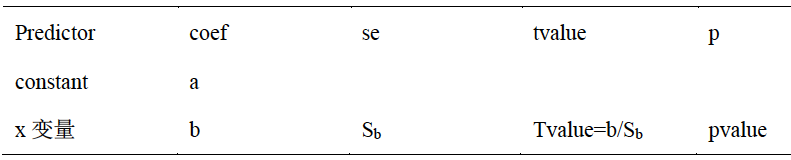例（2011年Form A） 
参考答案： 
（9）
例题
答案:E （10）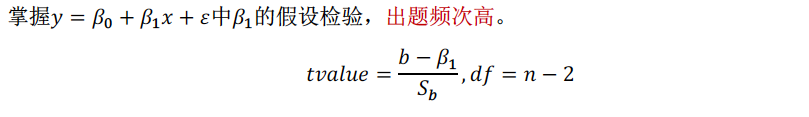
例（2011年From A） 
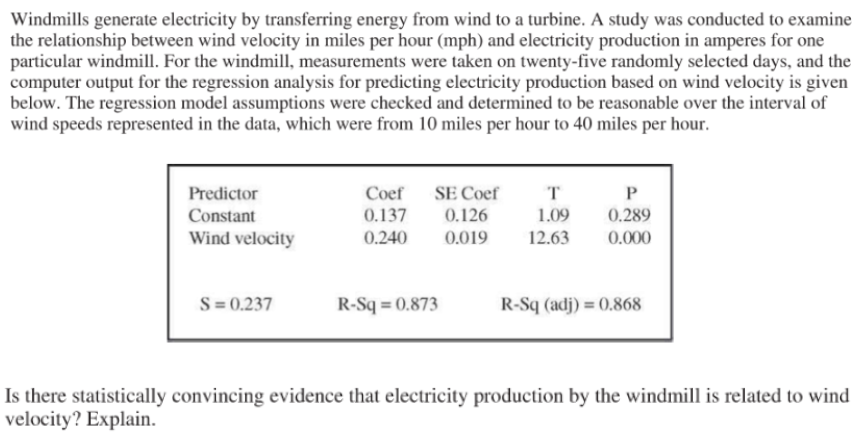参考答案：Yes, there is very strong statistical evidence that the population slope differs from zero, so electricity production is linearly related to wind speed. For testing the hypotheses H0:β=0 versus Ha:β≠0, where β represents the population slope, the output reveals that the test statistic is t=12.63 and the p-value(to three decimal places) is 0.000. Because the p-value is so small(much less than both 0.05 and 0.01), the sample data provide very strong statistical evidence that electricity production is linearly related to wind speed.
Unit 3 Data Collection
本章节基本会出4-5道选择题，1道简答题。
1. Sampling部分
（1）掌握掌握总体（population）和样本（sample）的概念，易出选择题。
（2）掌握随机抽样（random sampling）的几种方法，易考考点，简答题也会出陈述抽样过程以及比较抽样方法优劣的题目。 简单随机抽样（simple random sample）:会陈述如何抽取简单随机样本，简答题步骤一定要熟练掌握，考试频次极高。分层随机样本（stratified random sample）整群抽样（cluster sample）。系统抽样（systematic random sample） 例（2010年Form b）
参考答案： 
（3）掌握抽样中可能存在的error以及bias。抽样误差（sample error）：variability due to sampling.偏差（bias）：bias occurs when certain response are systematically favored over others. 特别注意仅改变sample size n，不会对bias产生影响，该点易考选择题。 涵盖不全偏差（undercoverage bias）、无回答偏差（nonresponse bias）、回答偏差（response bias）、选择偏差（selection bias）的概念需要了解清楚并掌握，能够根据题目信息判断陈述的属于何种偏差。 例
该题选 E
2. 实验（experiment）
（1）掌握观测研究和实验的本质区别，观测研究无法获得因果关系（cause-and-effect）可以通过设计良好的实验得到因果关系。特别是要清楚判断是观测研究还是实验，如果有treatment去treat实验对象，是实验。该考点易考。
（2）掌握实验对象、实验单位experimental unit，解释变量explanatory variable（也就是因子factor，因变量（response variable），混淆变量（confounding variable），区组（block，处理（treatment），对照组（control group）以及安慰剂组（placebo group）等的概念，能从一段陈述中选出以上概念指的是什么，该考点易考。 特别是混淆变量的定义一定要明确，既不是自变量，也不是因变量，但是也会跟影响因变量。明确在实验中存在混淆变量的最严重的后果是variation比较大，控制混淆变量的方式是划分block，其最主要的目的就是减少variation，该考点易考。 例（2010年Form A）
参考答案：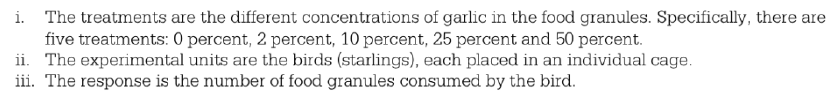 
（3）掌握设计良好的实验应该满足的几个要素，以及single blind 和double blind易考。
（4）掌握完全随机设计（completely randomized design），随机区组设计（randomized block
Unit 4 Probability，Random Variable and Probability Distribution
1. Probability
（1）掌握基本的概率概念。如果样本空间内的所有可能结果是等可能发生的，那么事件
（2） 掌握常见事件及其发生的概率，如补事件（complement）、交集（intersection）、并集（union）、互斥事件（mutually exclusive）、条件概率（conditional probability）以及独立（independent）的概念及公式，会灵活变通及使用这些概率公式。掌握以下公式：
这部分内容必考。 特别是将互斥和独立结合在一起的考点，基本每年必考。
例
参考答案：
（3）明确当题目中给出一个一般概率和条件概率时（这是判断基础，一定要看好题干信息），一定在考查tree diagram，高频考查的考点。
2. 离散型随机变量及其概率分布（discrete random variable and probability distribution）
（1）
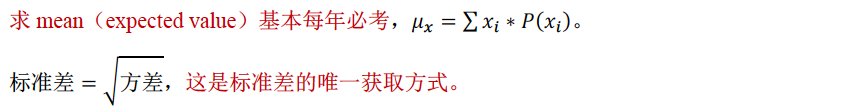
（2）与概率结合的考点，必考。 例（2015年）
参考答案： 
（3）与互斥和独立结合的考点，基本每年必考。
（4）binomial distribution考点每年必考。要掌握一旦n给定，success p给定时，要有倾向的往二项分布考点去判断。会熟练使用计算器binomial pdf和cdf求概率。会看公式表找其mean和standard deviation。 例（2011年 Form B）
参考答案： 
（5）geometric distribution考点近几年要关注，识别的关键first success的字样，掌握geometric pdf和geometric cdf。
3. 独立随机变量的组合（combining independent random variables）
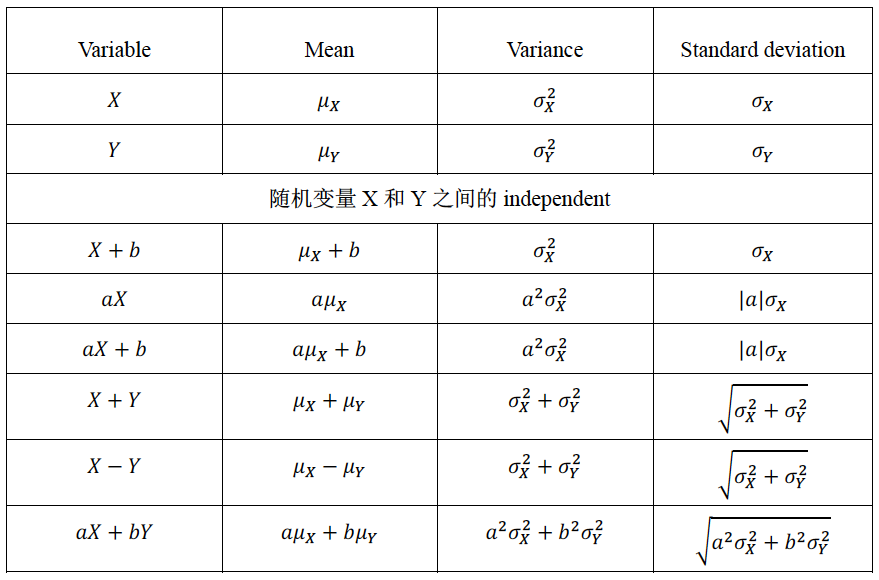
该考点必考，特别注意的是在变量之间组合时，样本标准差成立的前提是随机变量是独立的关系。 比如：注意不能用1个个体的10倍代表10个个体的和，因为世界上没有完全相同的两个个体。多个个体之间组合一定要用x+y的推广，不能用ax+by。 例 
参考答案：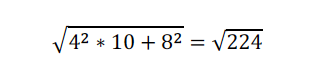
4. 连续型随机变量及概率分布（continuous random variable and probability distribution）
（1）掌握z-score的公式及其所代表的含义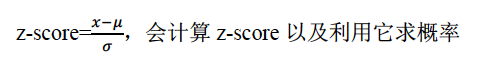 
这个公式特别重要，每年必考。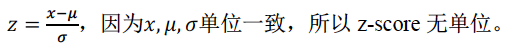 
（2）掌握zscore解释。如x value is 1.2 standard deviations above the mean value，意味着x value对应的zscore是1.2；如果将above变为below，zscore是-1.2，不容易识别，高频考查。
（3）掌握利用Normal cdf 求概率，以及在给定概率的前提下利用Inverse Normal求取值，每年必考。 例（2014年）
例（2009年Form A） 
（4）normal分布与combine independent variables结合的考点，有难度，每年必考。 
Unit 5 Sampling Distribution
1.明确中心极限定理（central limit theorem）的作用The Central limit theorem States that when the sample size is sufficiently large ,a sampling distribution of the mean of a random variable will be approximately normally distributed . 中心极限定理是将样本均值近似成正态分布的定理，而不是将样本近似成正态分布，很多同学在这里有误区，要区分好。
2.10% condition要掌握，如果样本量n小于等于总体容量的10%，那么可以基本忽略由于不放回抽样所导致的个体之间可能存在的关系，简答题必考。
3. 样本均值的抽样分布--掌握其正态分布的途径：normal population or large sample（n大于等于30），并且要会进行zscore进而求概率、inverse normal求value；large sample途径每年必考。 例（2010 From A)
参考答案 
4.结合公式表能找到样本比例、样本比例差、样本均值差的抽样分布对应的mean和standard error，并明确其分别实现normal的途径，该考点易考。 要特别注意：本部分内容一定会结合置信区间估计和假设检验进行考查。
Unit 6 Parameter Estimation
1.点估计（point estimate) 掌握一个好的统计量要同时满足无偏性（unbiasedness)和有效性（efficiently)，明确有效性对应variability of sampling distribution of statistic。 掌握，the best estimator 一定是无偏中波动最小的那一个。 例（2008年 from B)
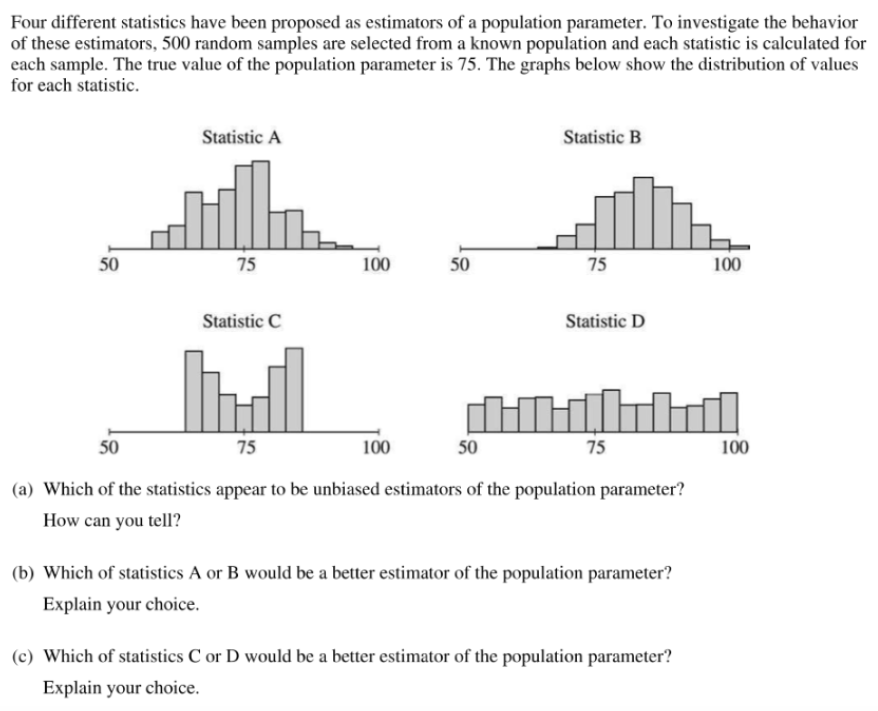参考答案： 
2.明确置信水平（confidence level）的基本概念并能结合题目的具体内容进行陈述，该考点必考一道选择题。 例confidence level =95%We can repeatedly take random samples from the population with the same size and construct 95% confidence intervals ,in the long run ,95% of the confidence internals will include the true population parameter value.
3.总体均值的置信间区间估计（confidence interval for population mean）
（1）明确当总体标准差已知时，采用单样本z区间对总体均值进行置信区间估计。掌握总体均值u的置信区间公式：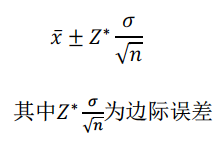 
最高频的考点为，给定margin of error求n，基本每年必考。 例
参考答案： 
The smallest sample size is 4979。
（2）明确当总体标准差未知时，采用单样本t区间对总体均值进行置信区间估计。总体均值的置信区间公式为：
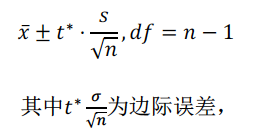
该考点非常高频考查，如考简答题一定要注意严格按照4步骤进行作答。 例（2013年）
参考答案 
4. 总体均值差的置信区间估计（confidence interval for the difference of two means）
（1）明确当两个总体标准差未知且不等时，采用双样本t区间对总体均值差进行置信区间估计，该考点易出简答题。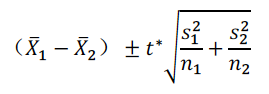 
其中，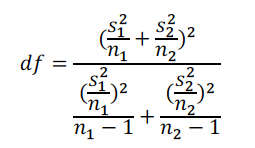
【注意：无需记忆df公式，先将计算器输入结果得到直接使用结果中的df即可】 例（2009年From A)
参考答案： 
5. 总体比例p的置信间区间估计（confidence interval for population proportion）
（1）明确对单一总体比例p的置信区间估计采用的是单比例z区间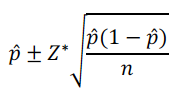 
熟练掌握构建总体比例p的置信区间估计的4步骤，能在简答题中根据题意快速写出步骤作答，本考点易考。
（2）掌握通过边际误差的给定值反求样本量n的题目，该考点也是易考点，基本每年必定会有求n的题目考点。 特别注意当p和未知时，代入p=0.5求解。 例（2011年From B)
参考答案 
6. 总体比例差的置信间区间估计（confidence interval for the difference of two population proportions）
（1）明确总体比例差的置信区间估计公式，采用的是双比例z区间。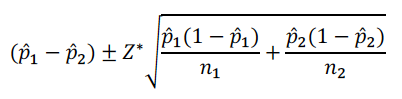 
（2）熟练掌握构建总体比例差的置信区间估计的步骤，能做到根据题意快速写出四步骤作答，该考点易考。 例（2009年From B) 
参考答案： 
7. 掌握matched pair sample对应的mean difference的求置信区间的4步骤。 考试时一定要区间好题目中是two independent samples 还是matched pair sample（one sample）。
Unit7 Hypothesis Test
1.假设检验（hypothesis test）的基本概念 （1）掌握零假设（null hypothesis）以及备择假设（alternative hypothesis）的概念，能熟练根据题目，快速写出对应的零假设和备择假设，该考点必考。
（2）掌握检验统计量（test statistic）和p值（p-value）的含义，该考点必考。
p-value是指在假定零假设为真的情况下，可以观测到的比根据样本计算出的检验统计量值至少更为极端的概率。并能够结合左尾检验、右尾检验以及双尾检验写出p-value的公式，解释p-value的含义。
2.总体均值的假设检验（hypothesis test for population mean）当总体标准差未知时，采用单样本t检验对总体均值进行检验，要熟练掌握检验4步骤，能根据检验结果，做出正确的检验结论，该考点高频考查。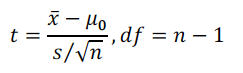 
例（2009年from b) 
参考答案 
3.总体均值差的假设检验（hypothesis test for the difference of two means）
（1）当两个总体标准差未知时，要采用双样本t检验对总体均值差进行检验，该考点必考。记住：计算器 two sample t test中pooled选No。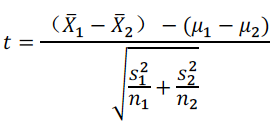 
（2）熟练掌握进行双样本t检验的步骤，并能结合题目信息，快速写出步骤进行作答。 例（2010年from A)
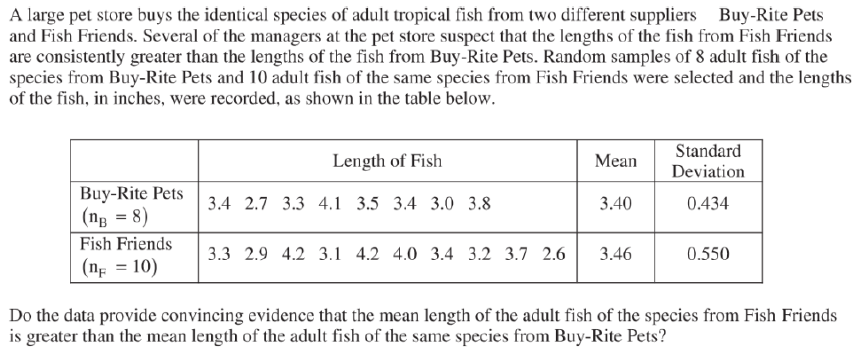参考答案: 
4.总体比例p的假设检验（hypothesis test for population proportion）
（1）明确对单一总体比例p的假设检验采用的是单比例z检验。
（2）明确总体比例p的假设检验统计量（test statistic）的公式
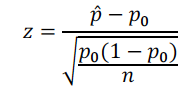注意：这里用的是，该考点高频考查。
（3）熟练掌握构建总体比例p的假设检验的4步骤，能做到根据题意快速写出步骤作答。
5.总体比例差p1-p2的假设检验（hypothesis test for the difference of two population proportions）
（1）明确对两个总体比例差p1-p2的假设检验估计采用的是双比例z检验，能根据题目写出假设。
（2）明确总体比例差的假设检验统计量（test statistic）的公式：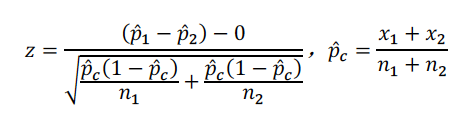 
（3）熟练掌握总体比例差p1-p2假设检验的4步骤，能够根据题意快速写出步骤作答。 总体比例差p1-p2假设检验的考点，非常高频地被考查。
6. 配对样本均值差的假设检验 掌握matched pair sample对应的mean difference的求假设检验的4步骤。 考试时一定要区间好题目中是two independent samples 还是matched pair sample（one sample）。
特别注意：在输入计算器是，t test中的u0输入0，该考点高频考查。 7. 假设检验中可能犯的两类错误（type I error 以及type Ⅱ error），考点必考 （1）熟练掌握下面的表格，能够结合题目信息写出type I error 以及type Ⅱ error。
Type I error是指we reject H0 but actually H0 is true。犯第一类错误的概率为α。
Type Ⅱ error是指we fail to rejectH0 but actually Ha is ture.。犯第二类错误的概率为β。检验的势（power of the test）为1-β。
（2）熟练掌握下面的表格，能够结合题目信息写出type I error 以及type Ⅱ error。 样本量n增大；显著性水平α增大；标准误差减少；真实的参数值远离零假设的假定值（真实值在Ha的方向上取值越extreme）。
8. 单尾检验和双尾检验的相互转换，对应的pvalue的不同变化情况，考点高频考查。
9. 假设检验和置信区间的关系
（1）明确confidence level+significance level=1
（2）明确如何使用置信区间对双尾检验进行简单结论的方法：如果零假设的假定值在置信区间外，拒绝零假设； 如果零假设的假定值在置信区间内，fail to reject 零假设。 该考点每年必考。 特别注意：置信区间估计只能跟双尾检验直接联系，如果想跟单尾检验产生联系，单尾检验必须先转成双尾检验。
以上就是老师为大家梳理的，复习的脉络和重点。希望大家在复习中不要跑偏，分配好各个AP科目的复习时间，做好规划，顺利实现考试拿5分的小目标！
