想要知道标题里的问题的答案?不知道上一期你有没有认真学习关于probability的基础知识呢?这一期我们将更深入地学习有关probability的规则和概念,然后再来解决标题里的问题~
本文目录
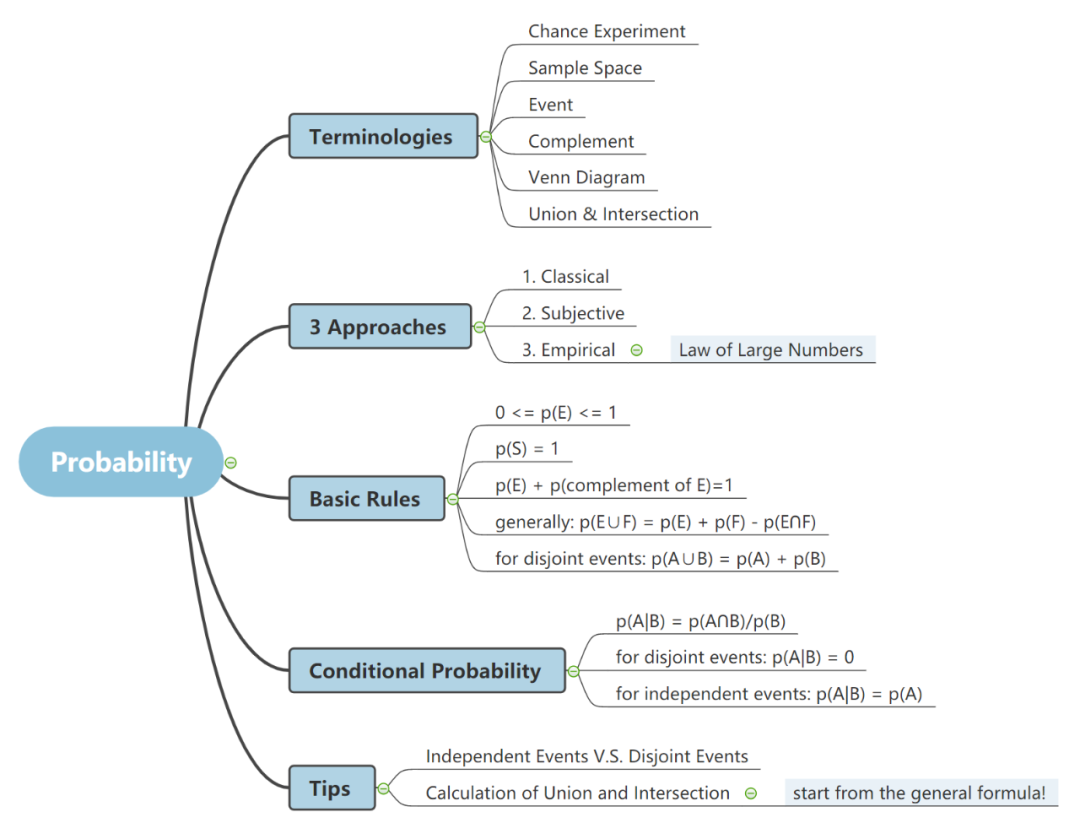
#Basic Terminologies of Probability
#Three Approaches of Probability
#Basic Probability Rules
#Conditional Probability
#Important Tips
Independent Events & Disjoint/Mutually Exclusive Events
Calculation of Union and Intersection
Part 3Basic Probability Rules
在概率中有一些非常基本的规则,这些规则有时能帮助我们完成很多概率上的计算。而且这些规则大部分都非常直观!
Rule 1 --- 关于合理范围内的概率值
对于任何事件E而言,0 <= p(E) <= 1
如果一件事完全不可能发生,p(E) = 0;如果一件事一定发生,p(E) = 1;剩下的可能性就是介于这两者之间,值越大某件事发生的可能性越大。 但你一定没有听说过有啥事情发生的概率是-80%或者120%的!
Rule 2 --- 关于sample space
p(S) = 1
简单来说,就是sample space里所有事件发生的可能性之和为1。(还记得上期的“荷包蛋”吧?整个黄框就已经框进了所有可能性。)
Rule 3 --- 关于completement
p(E) + p(EC)=1
还记得completement(补集)吗?EC就是所有除了E以外的结果的集合,那E和EC合起来就组成了所有可能结果的集合,它俩分别发生的概率之和肯定就等于1啦。
Rule 4 --- 关于概率加法的基本法则
对于两个事件E和F来说,p(E∪F) = p(E) + p(F) - p(E∩F)
为什么呢?给你个小提示:把E和F的Venn Diagram画出来。 画出来是这样的(见图5):
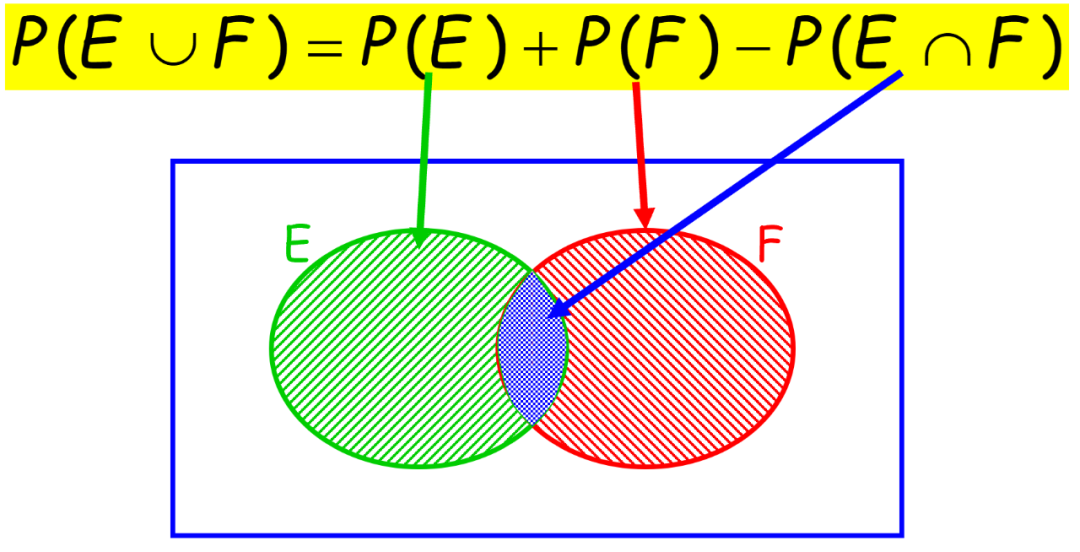
图5
是不是秒懂了?E与F的union(=E∪F=E or F)包含E、F以及它们相交的部分。然而p(E)+p(F)的时候中间重叠的面积被加了两次,所以要减掉一个p(E∩F)才能得到p(E∪F)。
Rule 5 --- 关于disjoint events的加法法则
好的,一段时间没碰骰子我又想开始扔它了。(骰子辛苦了!)想想这两个事件,A = {2}和B = {4}。当我一次扔一个骰子的时候,这两个事件有可能同时出现的吗? 当然不可以!我扔一次骰子,最后朝上的肯定只能是一个数字,不管是2还是4还是别的什么,但绝不可能是既2又4!
像这样的两个不可能同时发生的事件就被称为disjoint events(或者mutually exclusive events)。 请你想想,对于两个disjoint event A和B来说,p(A∪B)等于什么呢? 遇事不决就画Venn Diagram(见图6)。
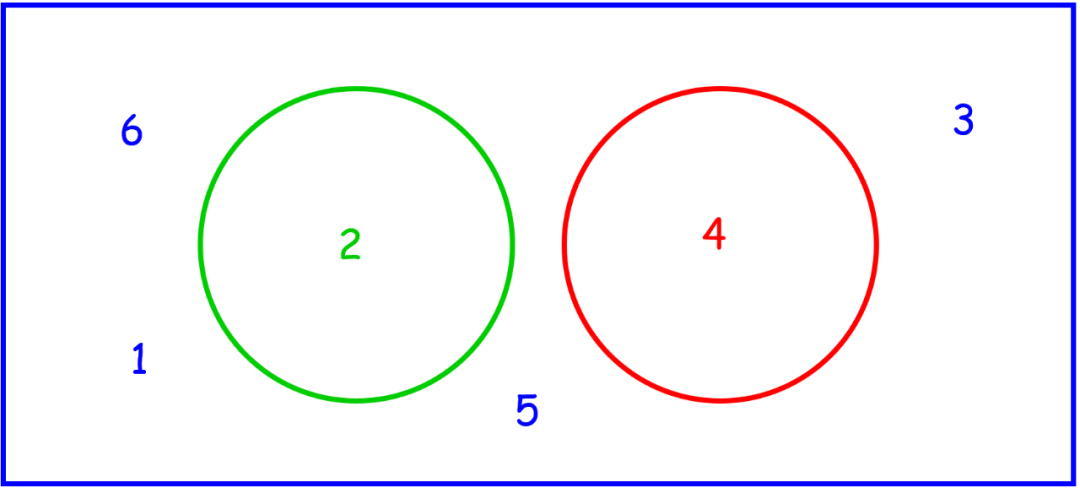
图6
啊哈!这个图跟前面的都不太一样呢,代表两个事件的圆圈居然没有相交!当然啦,因为A={2}和B={4}不可能同时发生,也就意味着p(A∩B) = 0! 那带入Rule 4里的概率加法法则,p(A∪B) = p(A) + p(B) - p(A∩B) = p(A) + p(B) – 0 = p(A) + p(B)。所以:
对于两个disjoint events A和B来说,p(A∪B) = p(A) + p(B)
是的,就是这么简单直接! P
art 4Conditional Probability
在之前抛骰子的例子里,当我们好奇某个数字朝上的概率时,我们列出来的sample space都包含了所有6种可能的结果,比如数字“4”朝上的概率就是1/6。 但是假如我瞟了一眼结果后偷偷告诉你,这次朝上的数字是个偶数,这时这个数字是“4”的概率还是1/6吗?(提示:考虑一下sample space有没有变化)
不是了!因为如果我们预先知道朝上的数字是个偶数,那么sample space就会发生改变,因为只有2、4、6是可能出现的结果,那么这个数字是“4”的概率就是1/3。
我们用A|B的方式来表示预先知道某些条件的结果,表示“当我们知道B发生的时候A发生了”,或者 “A given B”。 这就给大家举个例子 假如我们在一群学生中做调查,统计关于他们是否有在EP学习的经历以及AP统计是否五分的人数,收集到这些结果:
| AP统计5分:) | AP统计没有5分呜呜呜 | Totals | |
| 有在EP学习过! | 100 | 5 | 105 |
| 没有在EP学习过:( | 30 | 60 | 90 |
| Totals | 130 | 65 | 195 |
根据表格里的数据,请问在调研对象中随机抽取一位学生AP统计5分的概率是多少? AP统计5分一共有130位同学,总共调研了195位同学,p(5分) = 130/195 = 66.7%。
下一个问题!如果随机抽取的一位学生AP统计5分,那么ta在EP学习过的概率是多少呢? 首先AP统计5分是一个限定的条件。
然后我们来看,有多少位同学AP统计5分呢?130位。那既AP统计5分又在EP学习过的同学有多少位呢?100位。所以题目问的其实是在AP统计5分的条件下,AP统计五分和在EP学习过两种情况都满足的同学所占的比例:p(在EP学习过|5分) = 100/130 = 76.9%。
Conditional probability指的就是在条件B的限制下事件A发生的概率,即p(A|B)。它要怎么计算呢?很简单,p(A|B) = p(A∩B)/p(B),也就是A和B同时发生的概率/条件B发生的概率。
那么:p(在EP学习过|5分) = p(在EP学习过∩5分)/p(5分)=(100/195)/(130/195)=100/130=76.9%,和我们之前分析计算出来的结果是一样的√ 给同学们留个思考题:对于disjoint events A和B来说,p(A|B)等于什么呢?(答案请见文末思维导图)
【真题速递】(2017 Q7)

首先我们用Venn Diagram把题目中的已知情况表示出来(见图7):

图7
题目想让我们求的量是什么呢?风暴同时满足“originate in the Pacific Ocean” AND “be classified as major”这两个条件的概率。转化成统计语言,也就是计算p(PO∩M)。 观察Venn Diagram我们可以发现,因为PO有两种(Western & Eastern),所以p(PO∩M)其实就是p(WPO∩M)+p(EPO∩M),Venn Diagram这两部分之和(见图8):

图8
因为conditional probability可以通过p(A|B) = p(A∩B)/p(B)计算,把公式转化一下,就可以得到p(A∩B) = p(A|B) * p(B)。那么:p(WPO∩M)+p(EPO∩M)= p(WPO|M) * p(M) + p(EPO|M) * p(M)= 25% * 50% + 15% * 30%= 0.17所以答案应该选C!
【解题思路】
遇到概率题,我们可以做两件事:1)画Venn Diagram帮助分析(表示出已知情况+找到我们要求的量);2)把所有已知的概率条件列出来,看看我们能得到哪些信息。
Part 5Important Tips
5.1 Independent Events V.S. Disjoint/Mutually Exclusive Events
Independent Events(IE) 和Mutually Exclusive Events(ME)是比较容易混淆的一组概念。前面我们已经介绍了ME的概念,那么IE是什么呢?
如果一个事件的发生对另一个事件的发生没有影响,那么两个事件就是独立的,是一组independent events。 比如说你抛了一次硬币结果正面朝上(记为事件A),你又抛了一次硬币,这次正面朝上的概率(记为事件B)会被前一次的结果影响吗?
当然不会,不管你抛几次硬币得到什么样的结果,你下次抛硬币得到正面或者反面朝上的结果依然是50%,不存在什么硬币正面罢工了就再也不想正面朝上的情况。那么这里事件A和事件B就是一组IE,因为前者对后者发生的概率没有影响。
一组IE事件A和B有两个性质:
性质1:p(A|B) = p(A) 且p(B|A) = p(B)
因为A和B互相不会产生任何影响,所以加上|B或者|A这样的条件对彼此起不到限制作用,对另一个事件出现的概率也便没有丝毫影响。
性质2:p(A∩B) = p(A) × p(B)
这是一条可以用来验证两组事件是否是IE的重要性质!它为什么成立呢?想想如果A和B是两组正常的事件,那么上文有讲过p(A|B) = p(A∩B)/p(B) à p(A∩B) = p(A|B) × p(B)。如果A和B是IE,性质1提到了p (A|B) = p(A),带入上式不就变成了p(A∩B) = p(A) × p(B)嘛,正是性质2!
一组ME一定不是一组IE,因为ME意味着有你就没有我,有我就没有你,意味着一组ME 是会互相影响的,一个事件的发生情况取决于另一个事件的情况。那么反过来,一组IE也一定不是一组ME。 但是一组事件如果不是IE就一定是ME吗?不一定。因为ME只是两个事件互相影响的其中一种方式!
5.2 Calculation of Union and Intersection
关于union和intersection的计算,IE、ME和普通的两组事件所对应的公式看起来千奇百怪,但其实本质都是从普通的两组事件的计算方式推导出来的!相信下面这张总结图(见图9)可以很好地帮你解决如何应用计算公式的问题~
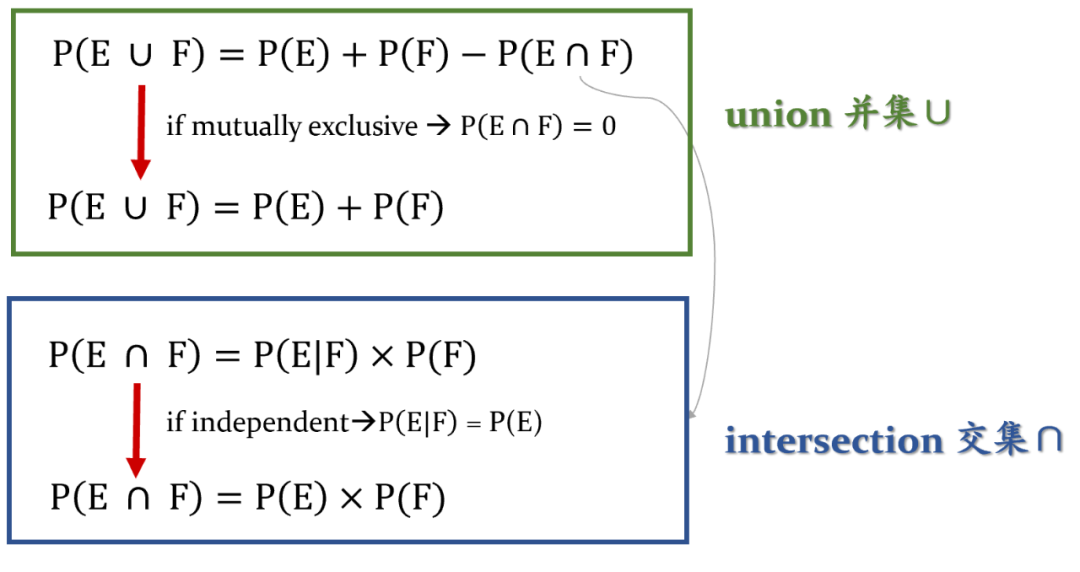
图9 【真题速递】 (2017 Q3)
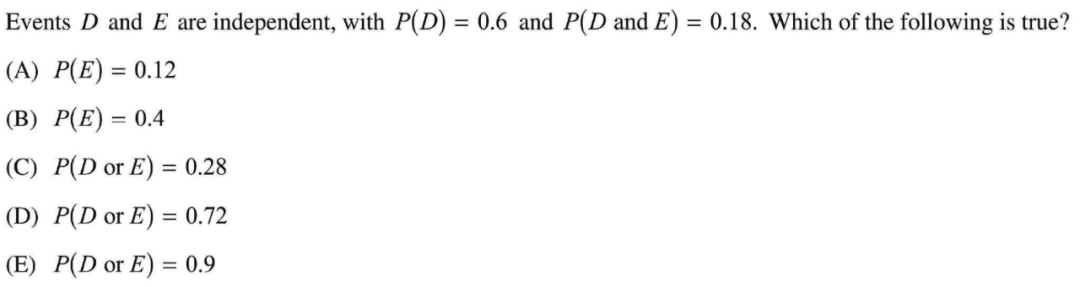
首先我们把已知条件列出来:D和E是independent events; P(D) = 0.6 ; P(D∩E) = 0.18。选项里需要我们计算P(E)和P(D∪E)。 对于independent events来说,它们的交集P(D∩E) = P(D) * P(E),所以P(E) = P(D∩E)/P(D) = 0.18/0.6 = 0.3。
接下来我们就要来求P(D∪E)。因为D和E是independent events,所以它们一定不是disjoint events,需要用通用公式计算并集,也就是P(D∪E) = P(D) + P(E) - P(D∩E) = 0.6 + 0.3 – 0.18 = 0.72。选择D!
所以5.2中的总结图还是很有用的,要记住噢!
结 语关于probability的讲解到这里就结束了~ 别忘了收下这份关于probability的思维导图总结~
噢对,还没结束。还有标题的问题没有解决呢。如果好奇的话请戳下面的链接~
有了这两期关于probability的讲解作为铺垫,相信你一定能够弄明白的!
https://www.thepaper.cn/newsDetail_forward_13497257