在这些考试中AP Calculus BC算是5分率最高的考试了所以今天就以学姐身份来跟大家唠唠嗑聊聊我们的主角——AP Calculus BC给到大家一些备考这门科目的经验分享和心得 如果看完这篇干货,仍有这方面的疑问或是想了解更多考试资讯,请咨询顾问老师哦~
本文目录
一、为什么选择微积分BC?
二、微积分BC的考试内容
三、学习及备考顺序:4步走
第一步:unit 1 极限的理解
第二步:从入门到怀疑人生的导数学习
第三步:从入门到放弃——积分
最终步:和Boss的对决——级数
01为什么选择微积分BC?
首先,作为妥妥的中国学生,数学一直是咱们“渴望驰骋学术疆场”的学科,所以选择报考微积分的考生也自然而然多了起来,更何况相比其他理科AP考试,微积分BC更容易拿到5分(感兴趣的小伙伴可以去查查AP Physics 1五分率……相信你可能即将捂着胸口回来)……
有些童鞋可能还在纠结微积分BC和AB究竟应该报哪个,但是如果告诉你BC不光有着惊人的44.2%五分率,AB仅有19%的五分率(均为2020年),且BC能买一赠一(考BC同时可得BC分和AB分哦),相信你内心一定已经做出了选择~
(但是还是要提醒一下在座童鞋们,BC除了涵盖了AB考试的所有内容,还增加了级数等相关章节,所以……如果想短时间抱佛脚的同学还是要慎重!慎重!毕竟报名费打水漂了真的会肉疼)
02微积分BC的考试内容
话不再多说,我们先来看一下最新AP Calculus BC的考纲内容:

其中,第六单元的积分内容和第十单元的级数内容为难度最大的部分,故需要童鞋们在这里付出更多精力。
03学习及备考顺序:4步走
我们都知道学习应该是一个循序渐进的过程,不能一口吃一个胖子;在学习备考微积分BC的时候也是同理。
作为一个已经走过备考微积分老路的过来人,我给大家推荐一下学习以及后期备考的顺序,希望大家能顺顺利利考个5分,开开心心给大学送申请!
第一步:unit 1 极限的理解
在开始学习微积分BC的时候,建议大家还是耐下心来踏踏实实打好基础(不要随便听信什么“一周速成微积分BC”这样的狂吠之语)。
所以,在学习微积分的开始大家一定要从Unit 1极限开始学习,为微积分系统学习打下基础。 注意我标题写的是“极限的理解”,所以大家在这部分单元一定要重点深入理解极限的含义和意义,而非仅仅学会做对题。
虽然仅仅做对题能够帮助大家更快拿到5分,但是理解极限的意义后大家在学习今后的导数、积分、泰勒展开、甚至大学学习的曲线积分等内容的时候才能更快的掌握。 在极限部分,推荐大家重点理解以下几点:
1. 极限的定义式

其中,一定要区分单侧极限和双侧极限哦~
2. 求函数极限的不同方法

3. 求函数渐近线的方法

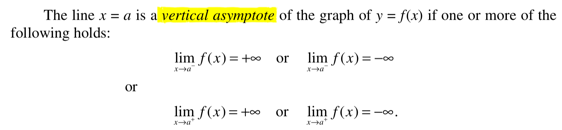
4. 连续函数的定义

当然了,作为极限重点内容,包含这几点的选择题也是在微积分BC考试中必被Q到的。所以,大家冲就完事了!
第二步:从入门到怀疑人生的导数学习
学习完极限,我恭喜大家已经成功入门微积分的学习。接下来要打败的是第一个也略有难度的小怪:导数。 导数包括的单元有2、3、4、5,其中第2、3单元为求导方法与计算,第4、5单元为导数的应用。
在刚开始的第2、3单元学习时,大家在沉浸于与导数卿卿我我的时候也不要忘记了曾经的好伙伴——连续。这其中就有经常考察的考点:函数连续与可导的关系。 这时候就要给大家推荐我们钟爱的一个表情包来辅助大家记忆理解:
连续不一定可倒(导),可倒(导)一定连续,不连续一定不可倒(导)
接着当我们来到第4、5单元时,大家一定要熟练重点记忆一下导数所求出来的函数性质,以下是为大家整合的思维导图帮助大家理解:
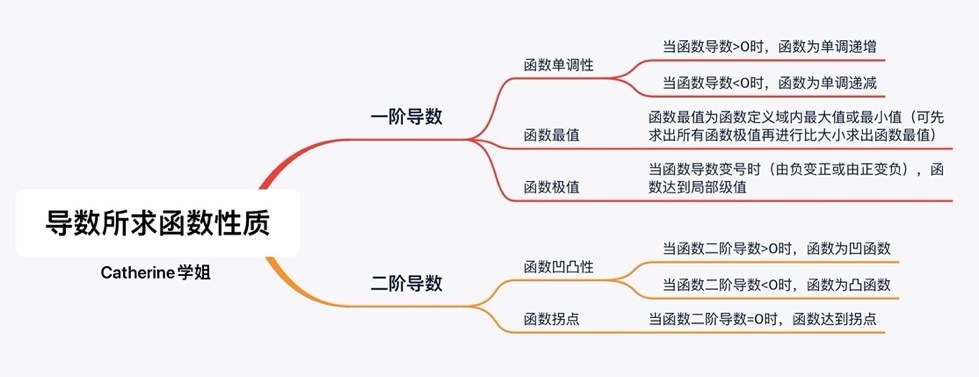
注意,这些函数一阶导数与二阶导数的运用是整个微积分考试中最重要的知识之一,每年的选择和解答都一定会出相关题目,所以要求同学们一定要熟练掌握运算技巧(比如说2020年就考了两道的FRQ)。
这里给大家列举一些题目案例: 比如下面这道题:
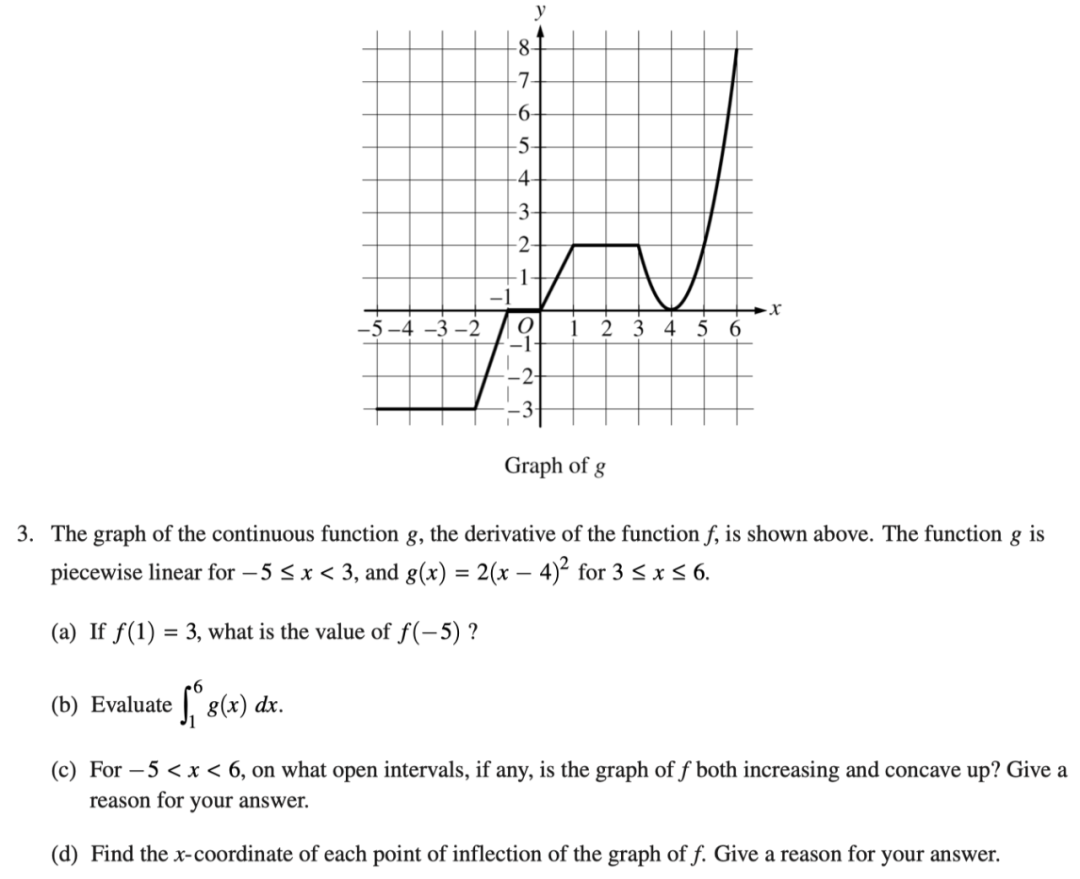
这道题是2018年AP Calculus BC的解答第三题。其中的c小问就考察了二阶导数计算函数凹凸性和拐点的内容。
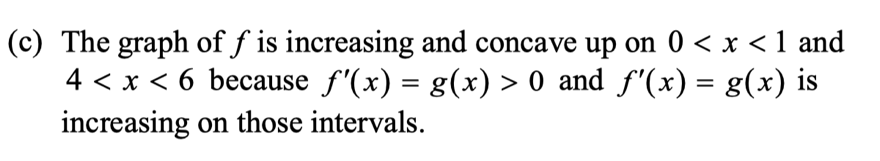
通过计算二阶导数,我们可以看出当0<x<1和4<x<6时,f’(x)>0(也就是g(x)>0),对应我们上面总结的思维导图可得知:在此区间内,f(x)为increasing;且在此区间g(x)为单调上升,可见f(x)二阶导数在此区间也为正,对应上方的思维导图可知f(x)为concave up。 除此之外,大家也一定要了解一下下面两个知识点:
1. 中值定理
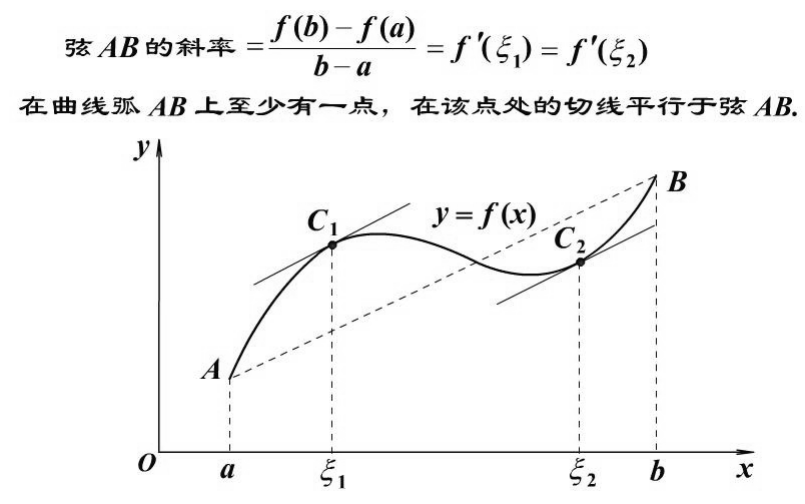
2. 洛必达法则

这些知识点属于每年必考但是考的数量并不多的题,每个知识点可能也就考一两道,不过学到就是赚到~
第三步:从入门到放弃——积分
接下来就是AP Calculus BC的重头戏:积分。 相比之前4、5单元的导数学习,积分更难,且其含义相当于导数的逆运算。
所以在熟练掌握积分的运算之前,大家一定要先理解透彻积分的含义,再背诵相关积分运算规则。在理解完积分的含义后,大家就可以开始牢记积分的经典公式啦!
必背型:(aka不背考场上后悔型)
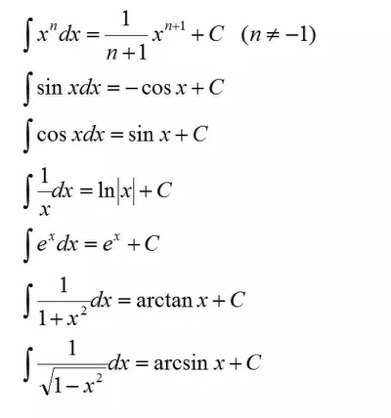
可背可不背型:(aka实在背不下来考场上可现推导型)
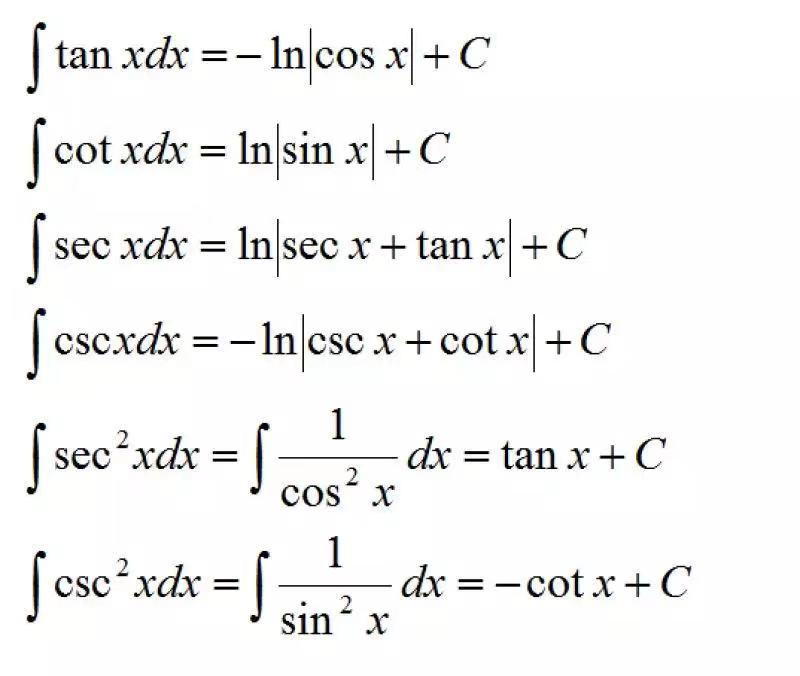
介绍完基础型积分运算,接下来就给大家上点有挑战性的题目练习下,嘿嘿~ 例题:(换元法)
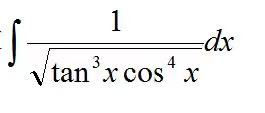
是不是有点蒙圈?没关系,让我们细(看)细(一)分(下)析(标)一(题)下: 没错!就是换元法!
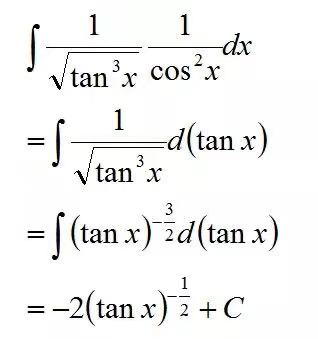
通过换元法,我们可以先将根号下cosx的四次方转化成cosx的平方,紧接着我们便能发现cosx平方分之一恰好就是tanx的求导。接下来我们只需要把这个积分问题看成tanx求积分的变形就可以了,是不是很简单~
所以,当我们遇到比较复杂的、看上去一眼无法解的积分题时,不妨联想一下换元法,把它变身为我们熟悉且会解的积分运算题目。 我仿佛已经听到有人在哀嚎了:那我怎么知道应该哪个换元?换成什么呀?所以呀,还是不要妄想自己是孙悟空能用火眼金睛一下看出正确解法了——吾等凡人还是把前面基础公式背牢吧!
(注意,所有的积分运算方法几乎都会在每次考试中被Q到,所以大家也别想偷懒了~)
最终步:和Boss的对决——级数
经过前面几个章节的披荆斩棘,我们终于来到了AP Calculus BC的boss关卡:级数篇。 这部分内容可以说是整个微积分BC系列最难理解的部分,很多同学在级数收敛性这部分就已经晕头转向了,更别说后面的泰勒级数、麦克劳林级数和拉格朗日误差的计算。
话不多说,先给大家一览Boss的一角面貌:(几个级数及收敛与否的相关结论)
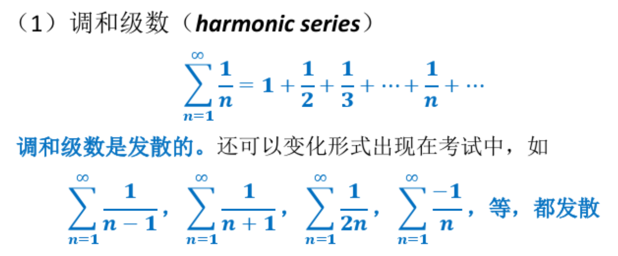




再给大家简单介绍一下我们“和蔼可亲”的泰勒级数:
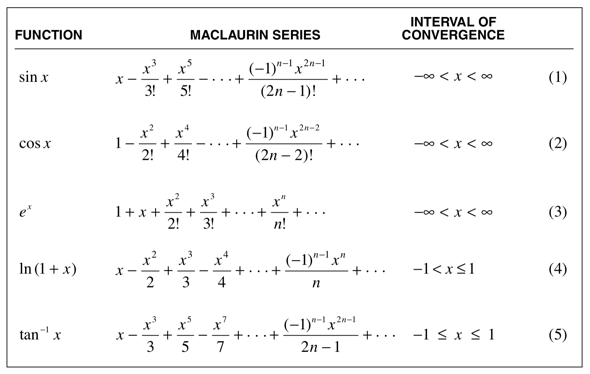
泰勒级数究竟是怎么产生的呢? 据说泰勒发现,幂函数是能够迅速求导求积分的函数(大家速速回想幂函数求导公式!!!),于是机灵的泰勒一拍脑瓜,如果所有的函数都能用幂函数表达,岂不美哉?
于是乎,伟大的泰勒级数就产生了。它的神奇之处就在于可以应用到几乎所有的函数中,而且使得函数的求导和求积分运算变得非常简单。
他的证明也非常有意思,主要运用的也是求导的内容,感兴趣的同学可以去查一下网上的视频证明,在这里就给大家放上当年我的证明过程叭~(图为证明sinx的泰勒级数)

可见,求泰勒级数就好像是用不同精度的尺子在跟我们所要求的函数比大小。当我们的尺子精度由x变为x平方,再由x平方变为x的三次方时,就能看出我们泰勒函数求出的结果越来越精确,距离真正sinx的函数也越来越接近。
总 结
好啦,以上就是AP Calculus BC的基本考试内容及学姐的备考经验分享啦。













