AP微积分BC5分备考冲刺指南

要考BC的朋友们大家好!上次大佛已经帮大家扫清了微积分AB的知识点，接下来我们的任务是快速回顾BC only的知识点，时间不多，赶紧往下看！

根据考纲 AP Calculus AB and BC course and exam description, BC only部分的知识点如下：

◆ 不定积分：分部积分、因式分解

◆ 反常积分

◆ 欧拉方法近似函数的数值

◆ 逻辑斯蒂微分方程

◆ 曲线弧长

◆ 参数方程组、极坐标、向量函数

◆ 级数

不定积分

1.分部积分

分部积分的公式如下：

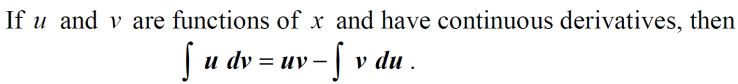
常考的分部积分题目如下：

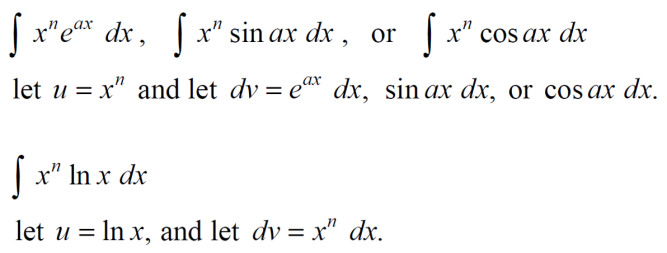
给大家列一道例题：

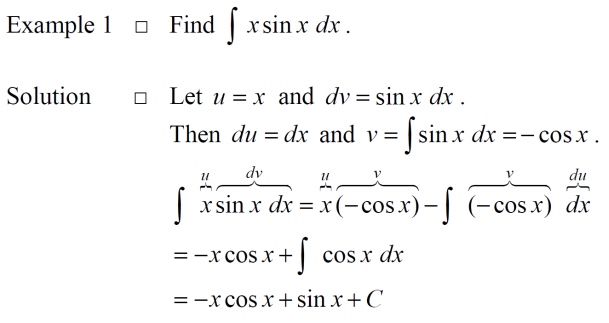
如果求解定积分的时候发现需要使用分部积分才能求出不定积分，则先不定积分然后再将上下限代进去求出定积分。
试看下方例题：

这里需要提醒大家，使用分部积分法交换积分位置之后，这道例题得到的是g’(x)对f(x)积分，这种情况下我们需要将d(f(x))展开，其实就是将f(x)对x求导，即d(f(x))/dx=f’(x)，d(f(x))=f’(x)dx。

2.因式分解

需要大家使用因式分解的方法求解不定积分的选择题选项都很明显，基本上都是ln|f(x)|：

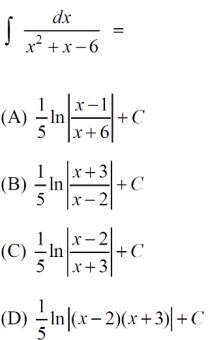
看到选项如此整齐划一的都有lnx和绝对值，那因式分解法求不定积分跑不了！

这里的因式分解是将一个分式拆开为两个分式，就是将题目中有两个因式的分母拆开为两个分式，分母分别为原分式的其中一个分式，然后用待定系数法求出拆开后分式的分子。

待定系数法示范如下：

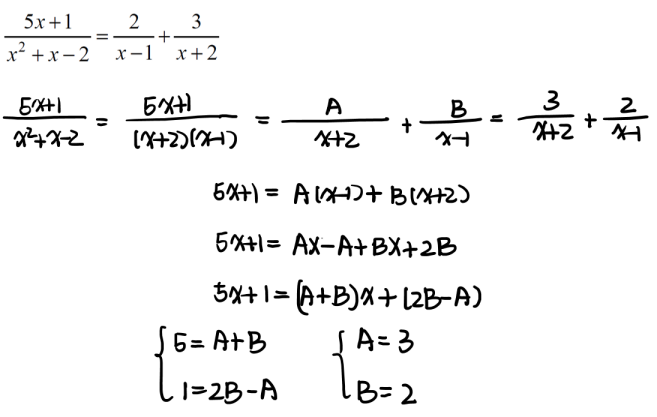
以及再次提醒各位对数函数的运算法则：

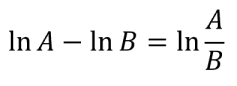
所以大家再看下最开始的例题，是不是感觉选项都给收起来了？最后一步就是用了对数函数的减法法则~

反常积分

反常积分有两种特征：

(1)第一种非常明显，即积分的上限或者下限出现无穷；

注意上方是如何改写积分限出现无穷的瑕积分：单独用一个字母（就别再用x了，x已经用来表示被积函数的自变量）替换出现在上限或者下限的积分，然后写一个极限的式子。

试看下面的一道例题：

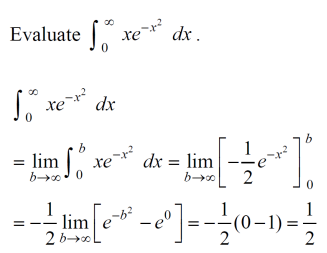
首先需要大家观察这个积分，上限出现了正无穷，判断此积分为improper integral；然后将其改写为带极限的积分；之后则先计算不定积分，最后一步是将上下限代进去计算极限的数值。

(2)第二种则不是那么明显，即被积函数无定义的点在积分的上下限所在的这个区间或者就出现在上下限。

第二种improper integral改写为极限的方式和第一种一样，都是将函数断开的点改写为单边极限的形式。

试看下方例题：

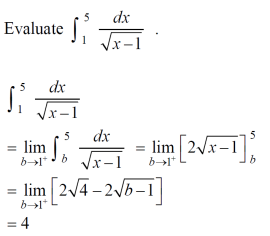
欧拉方法近似函数的数值

 

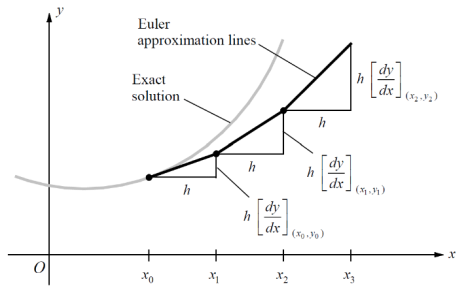
欧拉法则近似函数的数值简单而言就是多次线性近似，即运用这个方法需要使用两次甚至多次线性近似的公式。

试看下方例题：

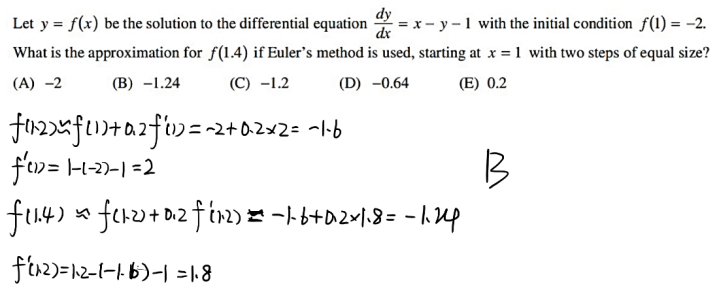
这里需要提醒两点：

第一点，题干中的two steps of equal size是指将从起始值(starting at x=1)和近似值(the approximation for f(1.4))的间隔分为两步等长的步长，即先从f(1)开始求得f(1.2)的近似值，然后再从f(1.2)求得f(1.4)的近似值。

第二点，f’(1)的数值从dy/dx的式子出发，题干已经给了条件f(1)=-2，即当x=1时y=-2，因此可以将其代入dy/dx的式子得到f’(1)；而f’(1.2)的数值则取决于f(1.2)的近似值是否计算正确，如果该近似值计算出错，最终的答案一定出错。f’(1.2)的数值同f’(1)，将x=1.2，y=-1.6代入到dy/dx的式子即可求得。

逻辑斯蒂微分方程

逻辑斯蒂微分方程的式子形式、各个字母所表示的意义需要大家非常熟悉：

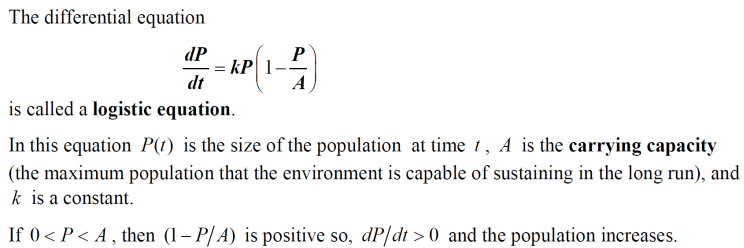
Carrying capacity A 中需要大家注意一个短语 in the long run，即长期下去人口数量会达到承载量，这种文字描述可以用下方的极限式子表示：

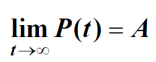
还有一些结论需要大家知道：

此外，逻辑斯蒂微分方程P与t关系的图像也需要大家熟悉，重点关注函数P(t)的凹凸性（先concave up再concave down）和增减性（increasing）。

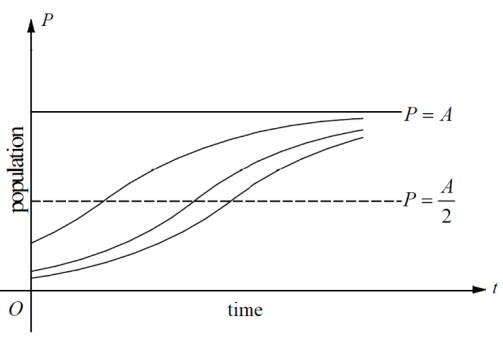
试看下方例题加深对上述知识点的理解：

曲线弧长

曲线弧长公式大家在最后的时间记住并知晓如何套用公式即可：

选择题考察该知识点一般只需要大家选择出正确的积分表达式：

如果是求给定范围的参数方程组的曲线弧长，下方所列公式和二维运动学中求某一时间段内的total distance公式一样：

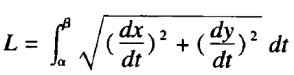
参数方程组、极坐标、向量函数

1.参数方程组的一阶导和二阶导

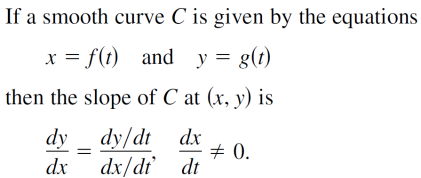
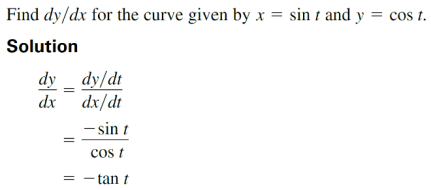
重点关注参数方程组求二阶导，简记为y’导除以x导：

 

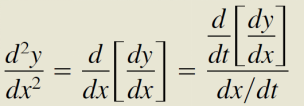
2.二维运动学

有个小问题需要大家注意，如何区分一维运动学和二维运动学？

A particle moves along the x-axis or straight path 即是一维运动学，因为物质在直线上运动；

A particle moves along the xy-plane 既是二维运动学，因为物质在平面内运动。

为何要特别予以区分？因为有的同学没能在一开始意识到物质是在直线还是在平面内运动，接下来的speed和distance套错公式。

此外，二维运动学还需要大家特别注意的是， position, velocity, acceleration都是以vector的形式给出来的，因此如果简答题中给的是velocity vector，要求在某一时刻的position（题目不会写position vector，一般会写find the position of the particle at time t=1这种），切记最后要以向量的形式（一般用圆括号，比如(2,3）这种)呈现答案。

二维运动学中position vector，velocity vector，acceleration vector这三者之间的关系同一维运动学，顺着都是分别求导，而逆着则是分别积分。

上述这道题是给position vector求velocity，则对position vector的x-component和y-component分别求导就行。

最后，还需要大家注意的是，二维运动学会考察大家distance，注意公式即可：

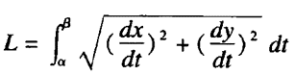
试看下方例题，看到求distance还不激动地搓手手！

3.极坐标

极坐标求导：需要特别注意直角坐标和极坐标的转化，以及极坐标求导其实就是参数方程组求导。

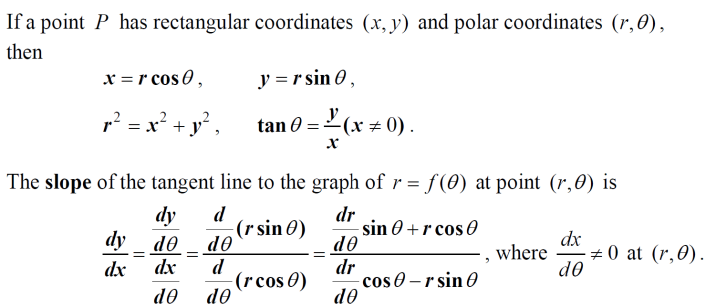
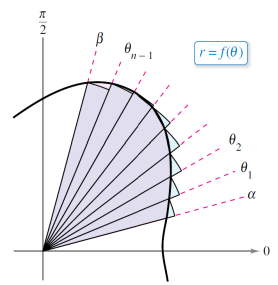
极坐标求面积：需要有一个扫过去的概念，试看下方图像，随着角度的增加，扫过的面积越来越多：

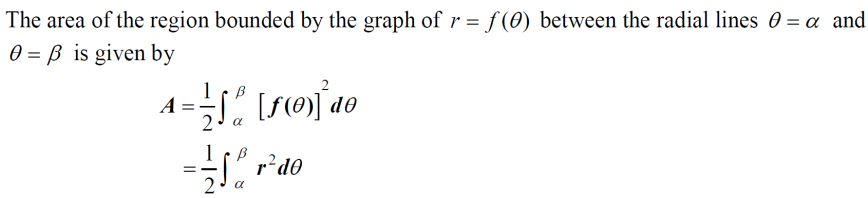
另外还有一点，极坐标求面积还会考察两条曲线包围的面积，一般是“大的减小的”，但题目中不乏有分割法求面积。

试看下方例题：

若要求两条极坐标曲线包围的区域所形成的面积，需注意：（1）求交点判断上下限；（2）判断两条曲线谁是谁，通过特殊点（角度为0，π/2，π）；（3）判断所求区域是否为“大的减小的”；（4）代入公式算值即可。

级数

级数这一块需要记忆的知识点尤其、特别、真的相当多！

1.几何级数

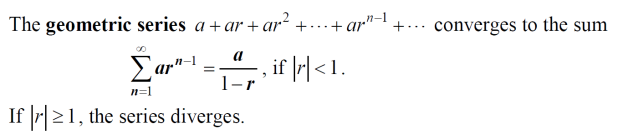
几何级数求值的公式中，a是首项（n=1），r是公比（后一项比前一项的数值），此外还需要特别注意，这是从第1项开始的！如果从第0项开始，需要单独计算n=0的值。

试看下方两道例题，注意区别：

级数从第一项开始加：

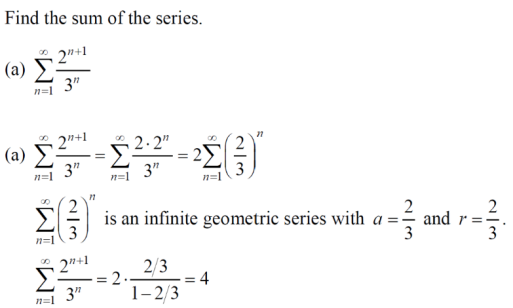
级数从第0项开始加：

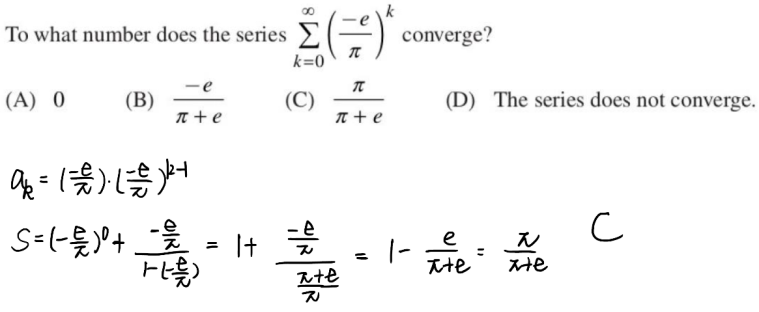
几何级数的收敛性取决于公比r的绝对值与1的大小关系，如果r的绝对值大于等于1，则该几何级数diverges，如果r的绝对值小于1，则该几何级数converges。

2.级数收敛判别法

（1）n-th term test

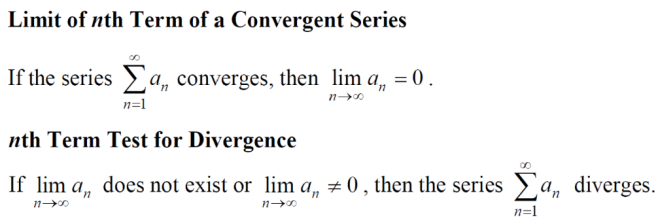
试看下方例题如何运用n-th term test判断级数diverges：

（2）integral test

积分判别法需要大家特别注意，不一定是从1开始积分，具体数值取决于级数从第几项开始。换言之，级数如果是从第3项开始，那么瑕积分improper integral的下限则应该是3。

试看下方例题，如果简答题出现Integral test，需要大家不假思索地默写条件，此外，大家还需要注意arctanx的常见特殊值和图像性质：

（3）p-series test

P-series和几何级数的收敛性判别条件刚好相反，且长相极其相似，很多同学区分不清楚，一般通过n（即表示级数的序数的字母）的位置是在底数还是在指数加以区分。如果n在底数，则为p-series（其他形式需满足条件），如果n在指数，则为几何级数。

（4）Direct comparison test

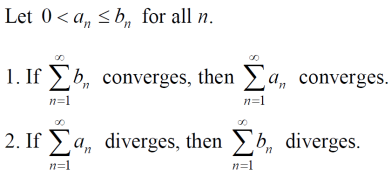
上述判别法可简记为：大敛小敛，小散大散。

（5）Limit comparison test

极限判别法需要特别注意，算出来的极限必须是一个正数，且不能为正无穷：

（6） Alternating series test

交错级数收敛性判别条件：

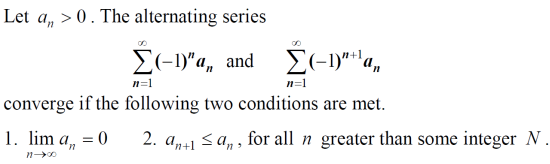
Alternating series识别较简单，通项必须有-1的n和n+1次方才能保证组成级数的每一项正负号不停变化。

此外，还需要注意alternating series的通项an大于0，不然其收敛性判别的第二个条件，前一项大于后一项，一正一负比较何从谈起呢？

交错级数的条件收敛与绝对收敛：

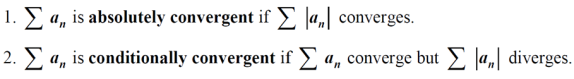
试看下方例题：

交错级数误差限：

Alternating series error bound处理为级数的下一项即可。

（7）ratio test

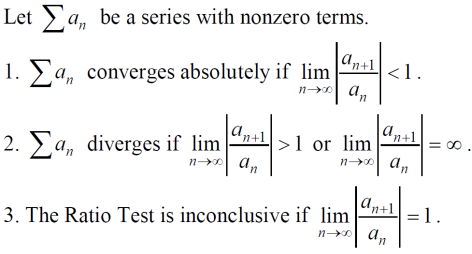
Ratio test一般用于各种奇奇怪怪的级数，比如阶乘和指数函数的组合、阶乘和多项式函数的组合、指数函数和多项式函数的组合。

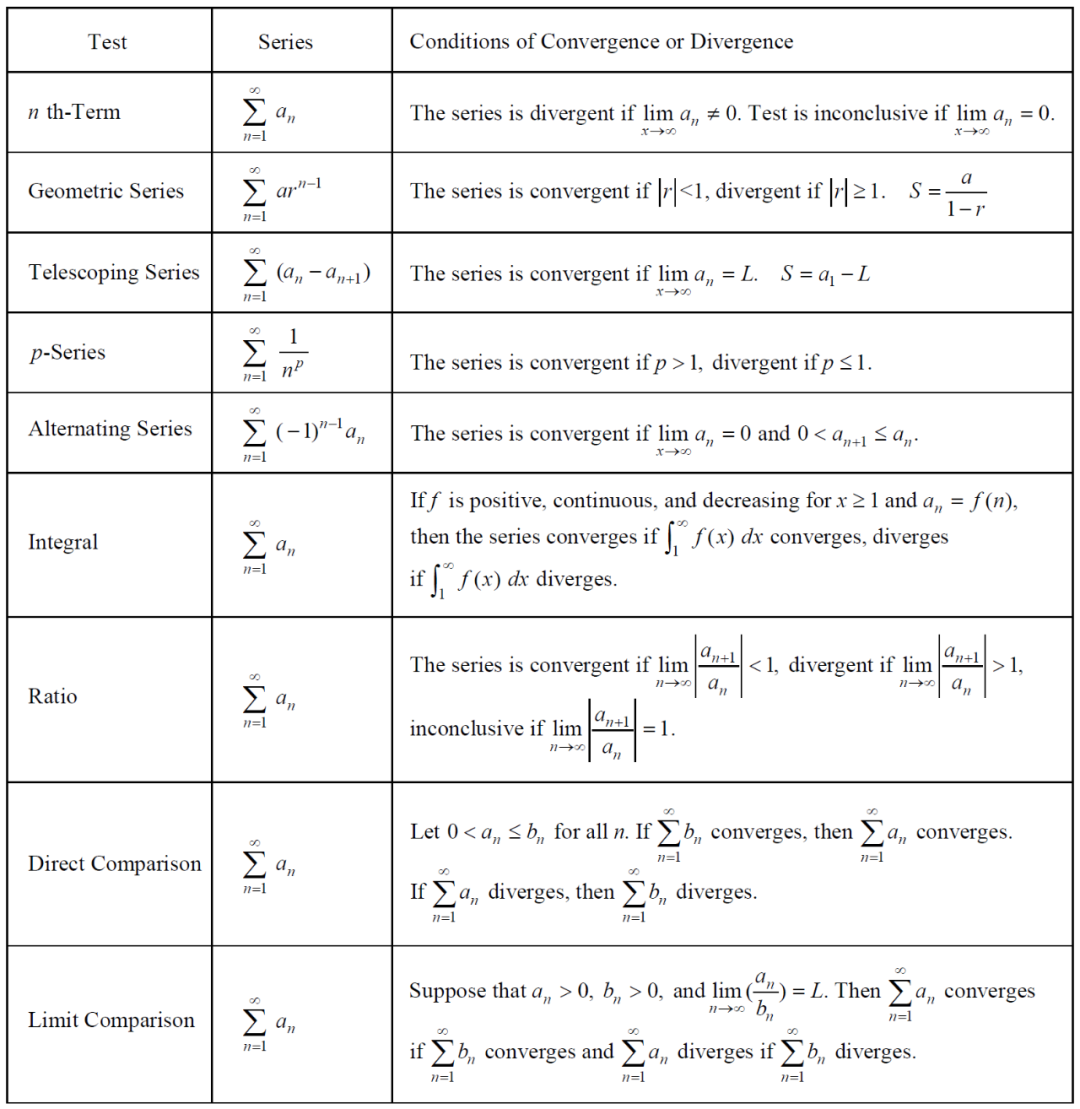
级数收敛性判别法总结：

3.幂级数的收敛区间和收敛半径

（1）幂级数的概念，简言之就是长这样的就是power series幂级数：

（2）The radius of convergence and the interval of the convergence of the power series:

收敛半径可处理为：用ratio test，取极限的倒数就为收敛半径。

收敛半径为|x-c|<R的不等式解集，此外，端点值还需要单独检验：

如果将端点处的数值代入原级数后收敛，则该处的不等式需要取等，如果发散，则不取等。

（3）幂级数的运算，运算包含求导和积分：

试看下方例题，注意不要被n干扰，因为这里的积分和求导都是针对x积分和求导：

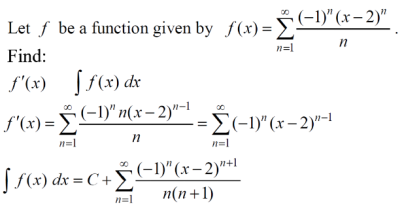
4.泰勒多项式（级数）和麦克劳林多项式（级数）

（1）泰勒多项式和泰勒级数的区别在于，前者加的项数为有限项，后者加的项数为无穷项。

泰勒多项式（级数）需要特别注意在何处展开，一般情况下题干的表述不会发生变化：the Taylor Polynomial/ Series for f about x=c。此外，题目还会让大家求某一项的coefficient系数，实际上是求n阶导除以n阶乘的数值：

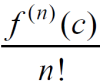
（2）需要大家记住常见的基本初等函数的麦克劳林展开式：

（3）泰勒级数还可用于近似函数的值，试看下方例题：

借用这道例题，需要解释几个在泰勒级数常见的术语：

The third degree Taylor polynomial是指需要将泰勒级数展开到第三阶，即该泰勒多项式x的最高次数（degree）必须为3；
The first four non-zero terms of the Taylor polynomial是指需要写出首四非零项, term表示项数。

（4）拉格朗日误差限，这里简单处理为下一项的最大值（实际上这里较复杂）。

试看下方例题：

最后的最后，请大家注意，级数的知识点非常之多，仅看上方知识点的摘要难以在短时间内掌握级数的知识，仅适用于自查知识点漏洞。要想级数的知识掌握程度更好，离不开一定题量的练习。

最后的最后，祝大家AP微积分BC考试顺利，功不唐捐，玉汝于成！