下个月就到了AP考试的时间了,大家在复习时是否清楚自己在知识点的掌握上还有没有疏漏呢?这篇文章总结了AP微积分AB和BC的考试要点,FRQ答题规范,并梳理了各章节核心知识点,给大家在复习阶段提供参考。
考前必看
1.要点总结
以下为AP微积分AB/BC中相对不容易掌握的知识点,检验一下自己的掌握情况吧。
·导数应用(图像):图像题融合了增减性,最值,凹凸性,拐点等众多知识点,对概念的清晰掌握和逻辑能力的要求都不低。
·导数应用(相关变化率):多个变量间的关系相对复杂,题目比较灵活,计算量也偏大。
·分部积分(BC):计算量偏大,系数容易出错。
·解微分方程:步骤较多,对计算要求比较高。
·极坐标(BC):与直角坐标差异较大,图像可能会比较复杂,将解析式转化成图像有一定难度。
·体积问题:需要一定立体图形想象力,抽象程度高。
·级数(BC):整章抽象程度都比较高,相对难以理解的章节,需要理解记忆的知识点也比较多。
2、FRQ答题规范

以2023年FRQ第一题为例,根据答案中的评分标准,在(b)问中得到满分需要列式表示出平均值,并得出正确答案。
需要同学们注意的是,即使是计算器部分的简答题,也要先列式再写出答案;一方面这样才能拿全步骤分,另一方面即使答案不准确,也不至于丢掉所有分数。

在更复杂的(d)问中得到满分,则需要写出完整的求global maximum的过程。可以看出,论述过程并不需要长篇大论的英语,同学们只要按照解题步骤把过程写清楚,在用数学符号表达不清时配合上一些少量英语表述即可。
过程的严谨才是得分的关键。尤其注意在使用Mean Value Theorem这样的定理时需要写清楚定理的条件,所以在复习时不要只关注定理的结论,也要注意在什么条件下定理才成立。
微积分BC思维导图
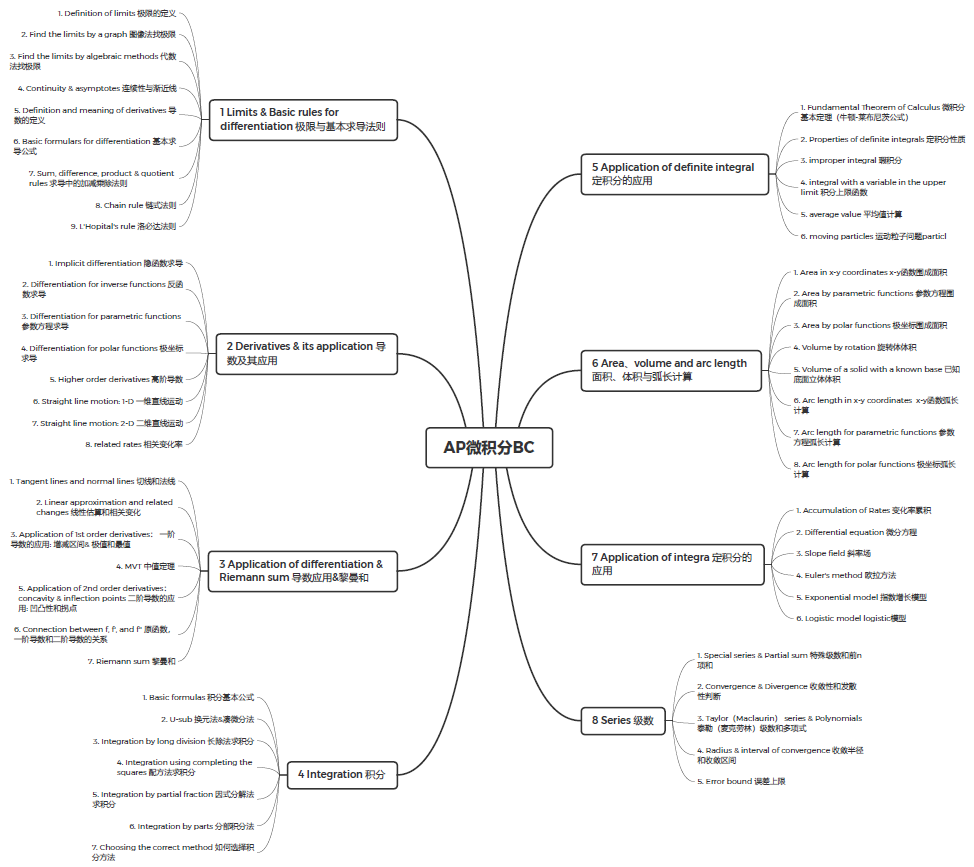
知识点梳理
1. 极限存在的条件:左右极限相等

2. 求极限:若代值可以得到结果则代值运算,若不能则选择以下方法
· 因式分解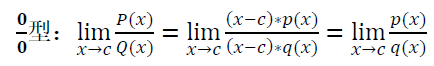
· 比较最高次项
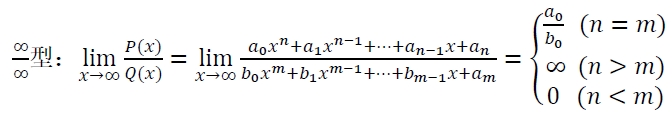
· 利用特殊极限
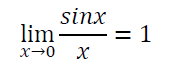
· 洛必达法则分子分母同时趋近于0或无穷时
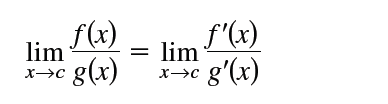
3. 夹逼定理
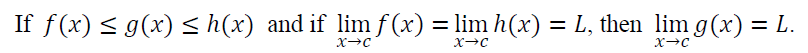
4. 渐近线
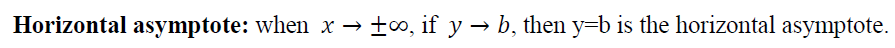
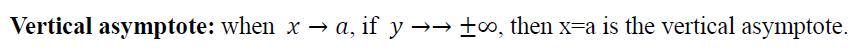 ▼例题:
▼例题:  本题答案为:C,求垂直渐近线时,需注意约分后再看分母何时为0 5. 连续性
本题答案为:C,求垂直渐近线时,需注意约分后再看分母何时为0 5. 连续性

▼例题: 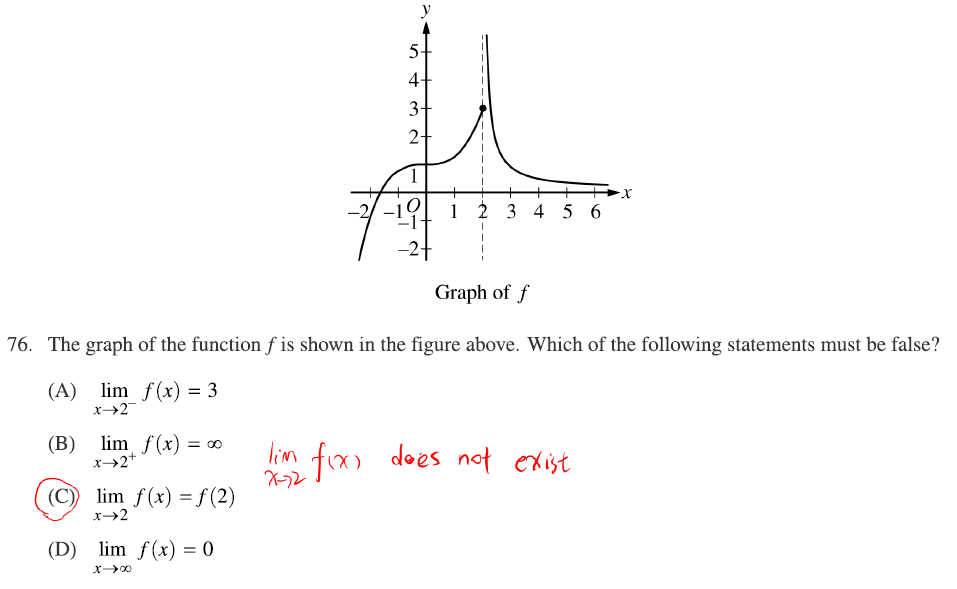 6.导数定义
6.导数定义

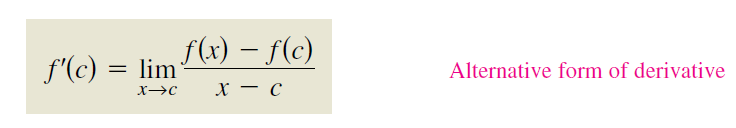
可导条件:

7. 导数运算公式
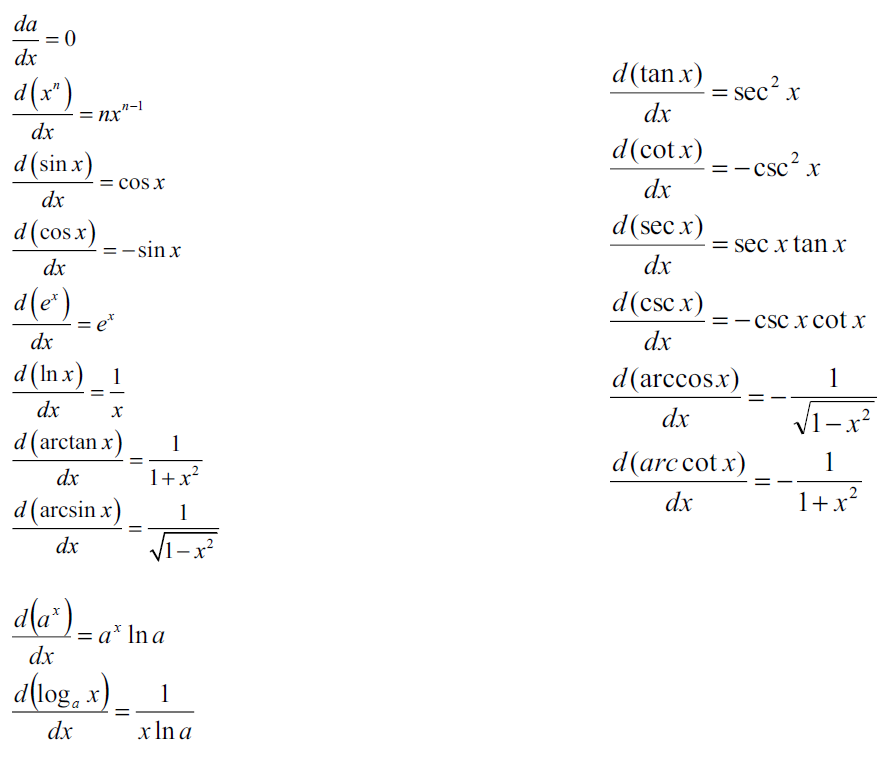

· 链式法则

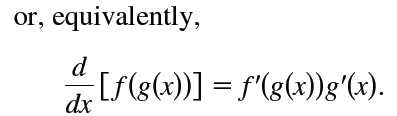
▼例题: 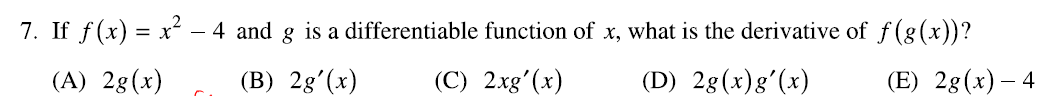 本题答案为:D8. 隐函数求导
本题答案为:D8. 隐函数求导


9. 参数方程求导(BC)
对于参数方程,可以分别找到x关于t的导数和y关于t的导数,再进行计算。
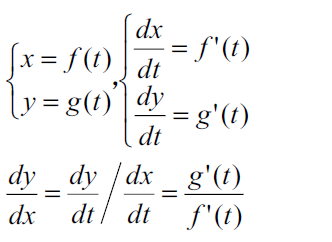
对于高阶导数,可以对一阶导数的结果再次求导即可得到二阶导。

▼例题 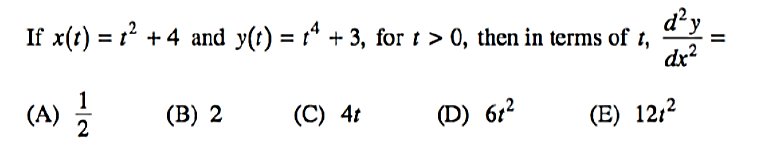 本题答案为:B10. 极坐标求导(BC)参考参数方程导数的做法,先把极坐标r,θ的关系转化为直角坐标x,y的关系,再按参数方程的做法求导。
本题答案为:B10. 极坐标求导(BC)参考参数方程导数的做法,先把极坐标r,θ的关系转化为直角坐标x,y的关系,再按参数方程的做法求导。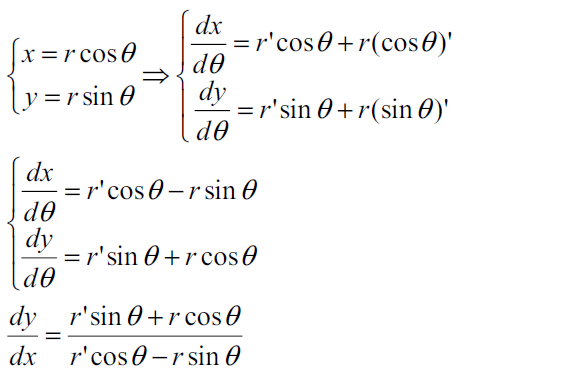
11. 增减性与极大/极小值
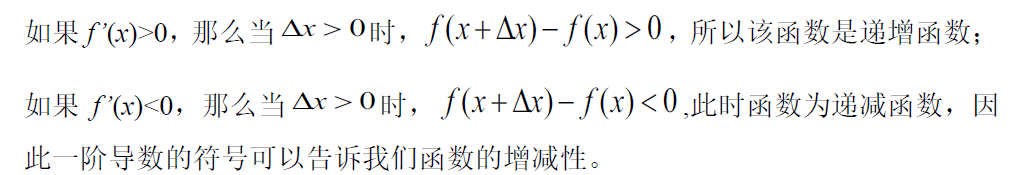
如果函数在某点由增函数变为减函数,那么该点在附近函数值最大,为局部极大值;如果函数在某点由减函数变为增函数,那么该点在附近函数值最小,为局部极小值。
· 找极值的步骤:(1)找到函数的一阶导
(2)找到导数为0或不存在的点
(3)判断导数符号的变化

如果找全局极值,则在以上步骤基础上,将符合条件的点和区间端点的函数值放在一起比较,得出最大/小值。
12. 二阶导,凹凸性和拐点

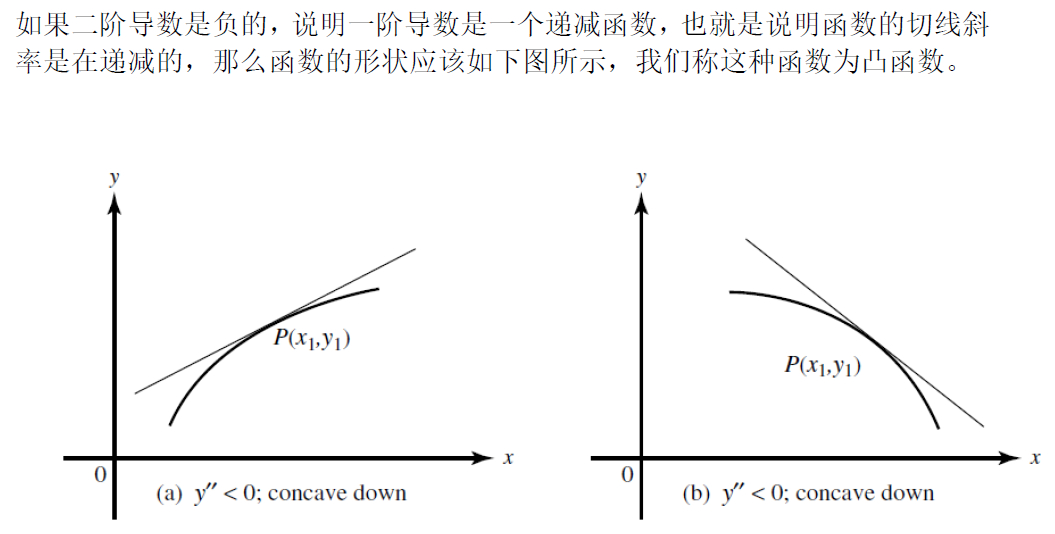
凹凸性发生变化的点称作拐点(points of inflection).
找拐点的步骤:(1)找到函数的二阶导(2)找到二阶导数为0或不存在的点(3)判断符号的变化,方法与一阶导数符号的判断类似。只要符号发生变化就是拐点,无论由+变-还是由-变+。13. 相关变化率

14. 介值定理,中值定理,极值定理

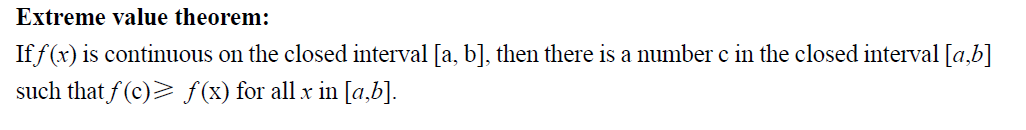

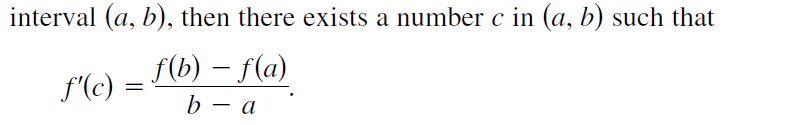 ▼例题
▼例题  本题答案为:C
本题答案为:C
15. 积分基本公式

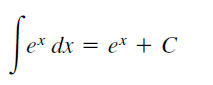

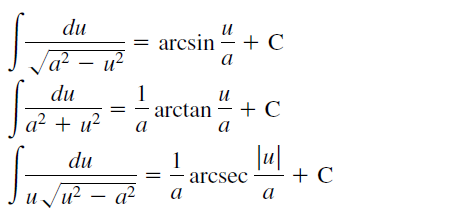
16. 积分换元法和配方法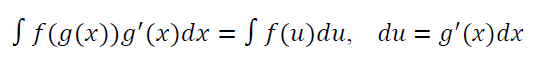 选取u时要注意u的导数应是原本被积函数的一部分。注:定积分的换元法要注意上下限的变化。配方法指的是利用与arctanx或arcsinx相关的公式来积分,通过换元凑成需要的形式。▼例题:
选取u时要注意u的导数应是原本被积函数的一部分。注:定积分的换元法要注意上下限的变化。配方法指的是利用与arctanx或arcsinx相关的公式来积分,通过换元凑成需要的形式。▼例题: 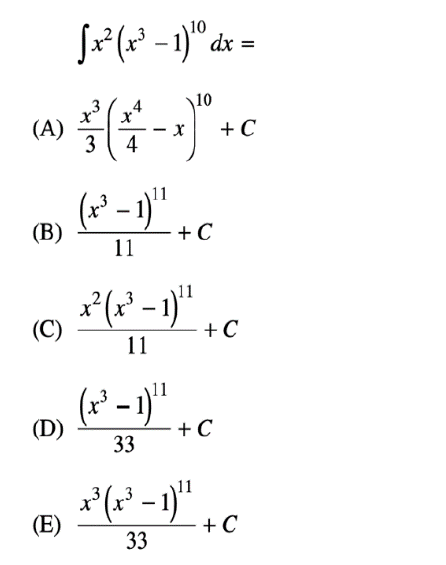 本题答案为:D▼配方法例题:
本题答案为:D▼配方法例题:  本题答案为:A
本题答案为:A
17. 分部积分法(BC)
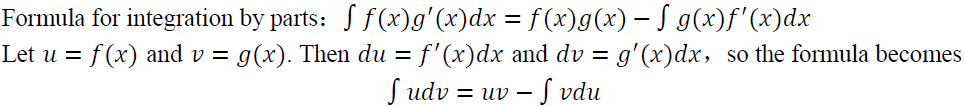 18. 因式分解法积分(BC)先通过因式分解把被积函数分成两项,再通过待定系数法确定分子的值。
18. 因式分解法积分(BC)先通过因式分解把被积函数分成两项,再通过待定系数法确定分子的值。
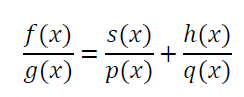
19. 黎曼和四种类型:- LeftRiemann Sum:
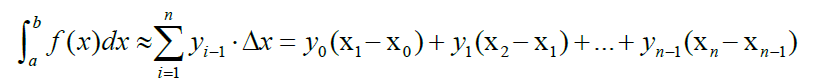
- RightRiemann Sum:
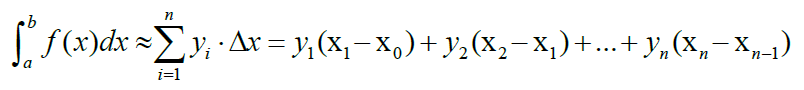
- Midpoint Riemann Sum:
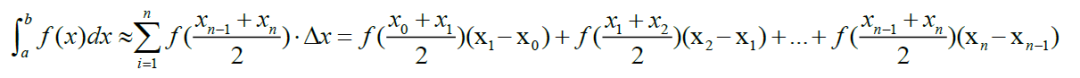
- Trapezoidal Riemann Sum: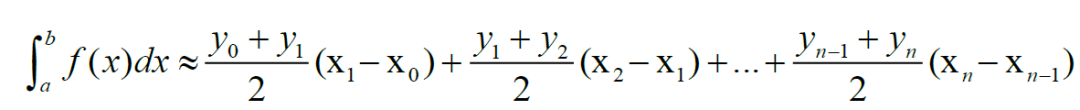
定积分与求和形式转化:
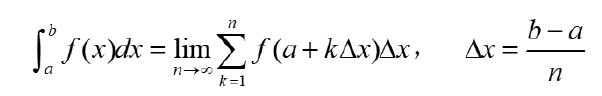
20. 微积分基本定理
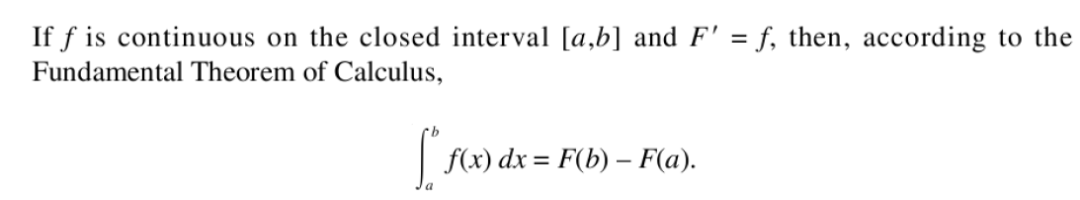 此定理为定积分运算的依据。
此定理为定积分运算的依据。
▼例题: 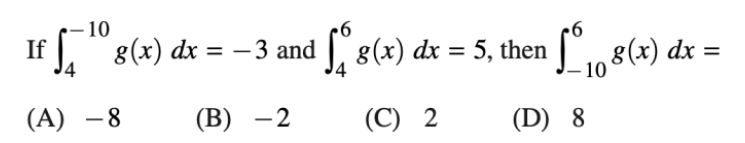 本题答案为:D
本题答案为:D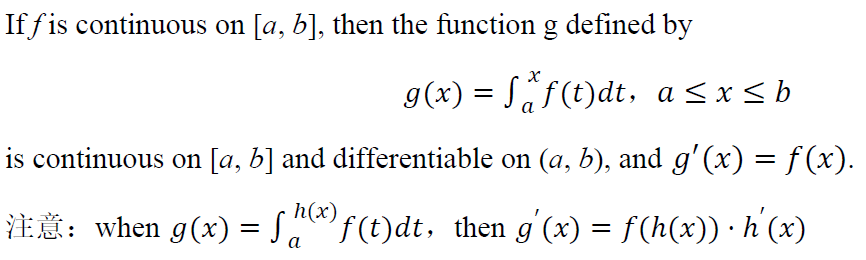 在积分上限函数中,f(x)是g(x)的导数,g(x)是f(x)的原函数(反导数)。▼例题:
在积分上限函数中,f(x)是g(x)的导数,g(x)是f(x)的原函数(反导数)。▼例题: 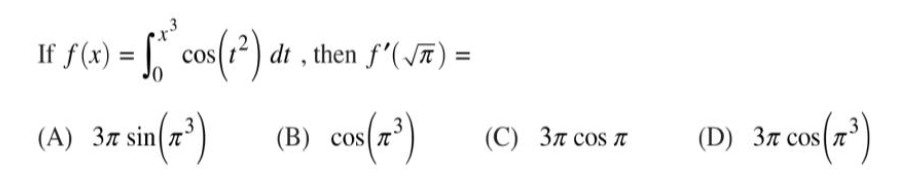 本题答案为:D
本题答案为:D
21. 平均值
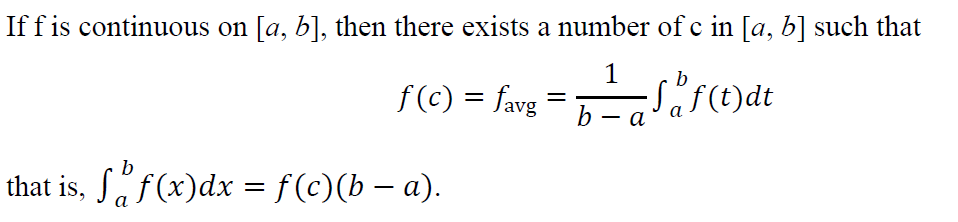
22. 反常积分(BC)
积分区间无穷或积分区间内函数无界时,用极限来表示积分的区间
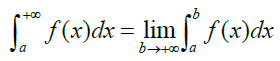
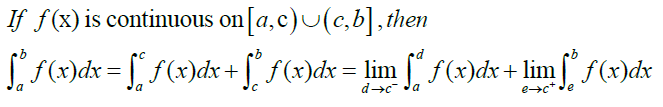
23. 平面面积
以x为积分变量时,用包围阴影图形的上面曲线减下面曲线
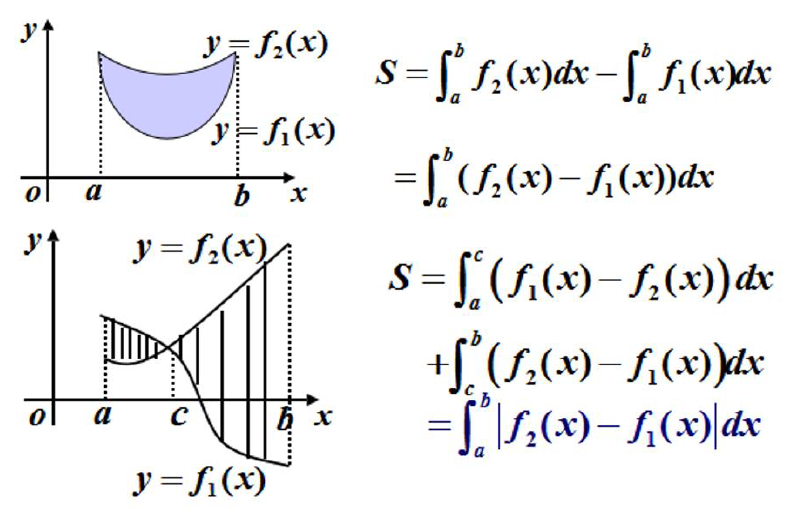
以y为积分变量时,用包围阴影图形的右面曲线减左面曲线
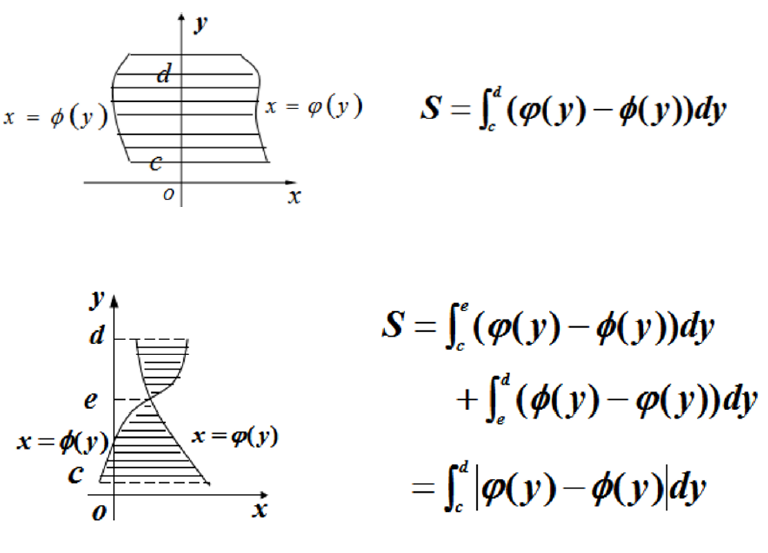
24. 立体体积(1)旋转型体积旋转型包括没有空心的disk method和有空心的washer method。
- Disk method:
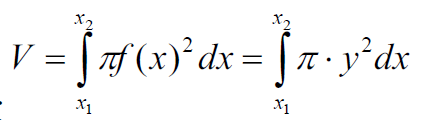 - Washer method:
- Washer method: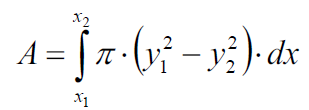 若旋转轴为与坐标轴平行的直线,积分中截面圆的半径用函数与旋转轴的距离表示。选择积分变量看旋转轴与哪个坐标轴平行或重合(例如绕x轴旋转则对x积分)
若旋转轴为与坐标轴平行的直线,积分中截面圆的半径用函数与旋转轴的距离表示。选择积分变量看旋转轴与哪个坐标轴平行或重合(例如绕x轴旋转则对x积分)
(2)截面型体积
用函数表示截面的面积,并对这个函数积分。
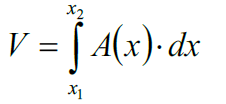
积分变量选择看截面垂直于哪个坐标轴。
需要掌握正方形,长方形,半圆,等边三角形和等腰直角三角形面积的计算公式。25. 极坐标面积(BC)
极坐标函数包围的面积计算公式:

两个极坐标函数之间的面积公式: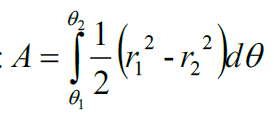 积分区间可以通过观察图形的角度范围以及列方程计算θ的范围。26. 弧长平面内曲线弧长:
积分区间可以通过观察图形的角度范围以及列方程计算θ的范围。26. 弧长平面内曲线弧长: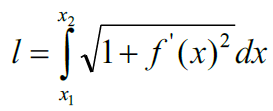
参数方程曲线弧长(BC):
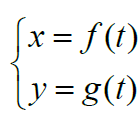
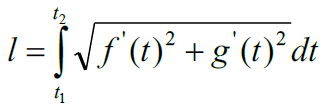
27. 运动问题
总距离,位移,速度,加速度,速率间的关系:

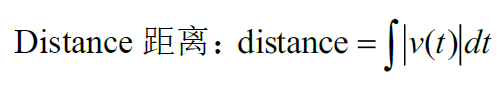 二维运动(BC):二维运动问题结合参数方程来考虑,位移,速度,加速度都分为水平方向和垂直方向计算,以向量形式表示,如position vector可表示为
二维运动(BC):二维运动问题结合参数方程来考虑,位移,速度,加速度都分为水平方向和垂直方向计算,以向量形式表示,如position vector可表示为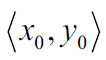 这些向量的大小利用勾股定理把两个方向组合起来表示,比如求speed就用
这些向量的大小利用勾股定理把两个方向组合起来表示,比如求speed就用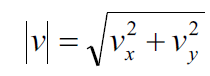 来表示。求total distance的问题用含参数的平面弧长的公式来解决。28. 解微分方程解形如
来表示。求total distance的问题用含参数的平面弧长的公式来解决。28. 解微分方程解形如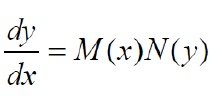 的微分方程步骤1:分离变量
的微分方程步骤1:分离变量
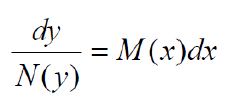
步骤2:对等式两侧积分
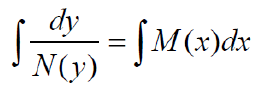
步骤3:积分后整理式子成用x表示y的形式,并代入特殊值求出常数C
29. 线性估算
用函数上一点的切线来估算切点附近的函数值f(x)≈f(x₀)+f'(x₀)(x-x₀),
,x₀为切点的横坐标。
欧拉法(BC):分段并重复多次的线性估算。
▼例题: 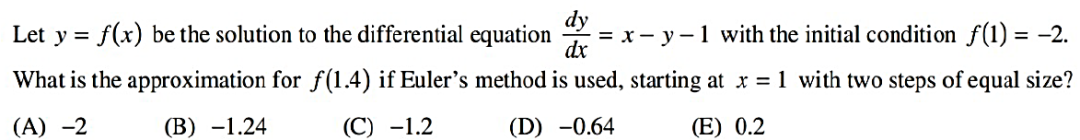 本题答案为:B
本题答案为:B
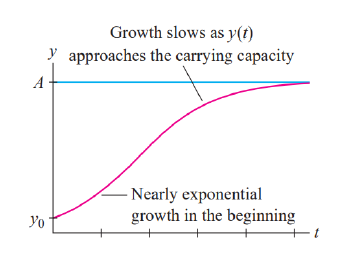
30. 指数增长和logistic growth
指数增长模型: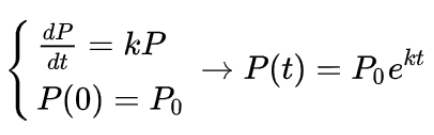 P0为t=0时函数的初始值,符合此模型的函数即为指数增长。关键词:增长率与函数值成正比(proportional)Logistic growth 模型(BC):
P0为t=0时函数的初始值,符合此模型的函数即为指数增长。关键词:增长率与函数值成正比(proportional)Logistic growth 模型(BC):
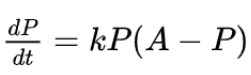
A的值为函数在t趋近于无穷时的极限。
函数值在到达A/2后,增长速度开始变缓。
31. 级数(BC)
判断级数收敛:
(1)N-th term test

(2)Geometric series test
几何级数在|r|>1时收敛,≥1时发散。
(3)P-series test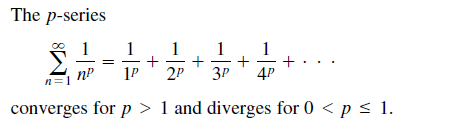 (4)Integral test
(4)Integral test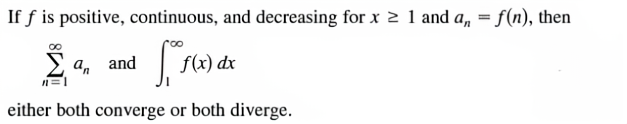 注:积分的值与级数值不完全相等。
注:积分的值与级数值不完全相等。
(5)Comparison test
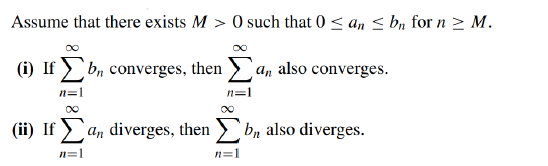
(6)Limit Comparison test
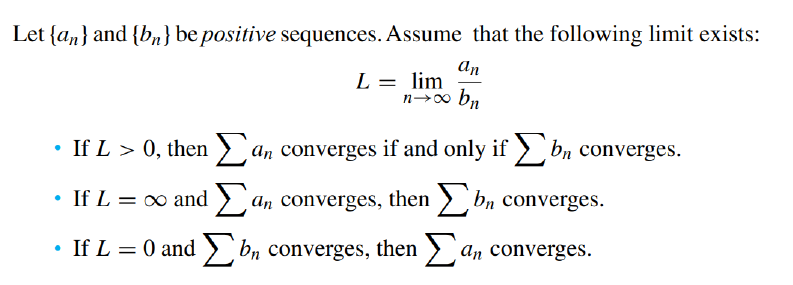
可以用于分式形式级数的判断,根据分子分母最高次数的差来选择相匹配的p-series,则级数与这个p-series收敛情况相同。(7)Ratio test
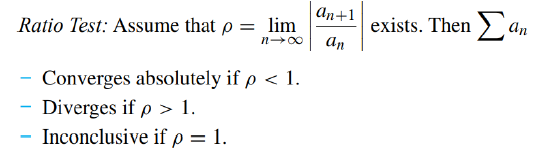
多用于含有阶乘和指数函数的级数判断收敛,也在计算power series收敛区间时使用。
(8)Alternating test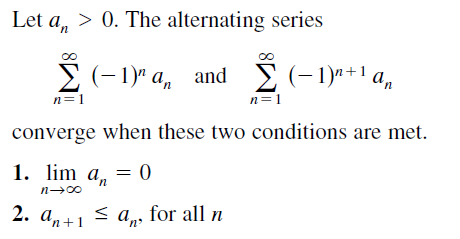
注:第二个条件指的是数列绝对值递减,不需要考虑符号。
级数收敛判断方法的选择:
先判断级数的类型选择对应类型的方法,比如交错级数直接用alternating series test 判断。
其他情况:含有指数函数,阶乘的级数选择ratio test;多项式分式选择limit comparison test;与已知是否收敛的级数有严格的大小关系时可选择comparison test;题目明确提出或比较容易积分时可选integral test。
几何级数求和:
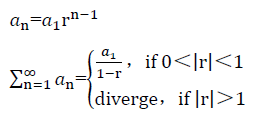
几何级数的公比r由第n项和n-1项的比值得到。收敛的几何级数可以用公式求和。
▼例题: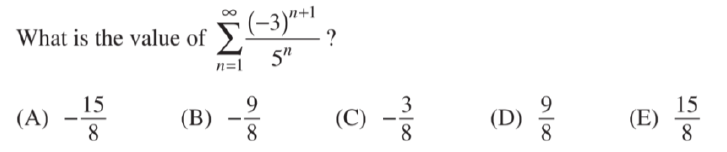 本题答案为:D
本题答案为:D
收敛区间和半径
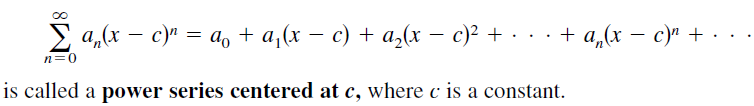
x=c为power series的收敛中心,在距离c收敛半径r以内的范围内的x都可以使级数收敛,这个范围就是收敛区间。
计算收敛区间步骤:1.令用ratio test得到的比值结果小于1,并解不等式2.不等式的解为级数absolutely converge的范围,分别将边界值代入原级数判断是否收敛3.若边界值收敛则包括在区间内,发散则不包括注:converge conditionally的x值位于收敛区间的边界▼例题:  本题答案为:B
本题答案为:B
泰勒级数和误差上界
泰勒级数和麦克劳林级数计算公式:

注:题目中泰勒级数的degree指的是最高次数,non-zero terms指的是包括几项。
需要知道的麦克劳林展开式:

泰勒级数除了直接通过公式求导计算得出,还可以由已知展开式加减,乘常数系数,求导,积分,换元得到
Alternating error bound:
 交错级数的误差上界为所取的级数的下一项的绝对值。计算error bound只需要从题干按关键词中提取信息代入公式即可得出结果。
交错级数的误差上界为所取的级数的下一项的绝对值。计算error bound只需要从题干按关键词中提取信息代入公式即可得出结果。
考前寄语
五月AP考试在即,同学们在复习阶段要有规划的做一些题目,最好能计时完成整套真题来适应考试的形式和节奏。刷题时一定注意改错和复盘,总结自己哪些知识点掌握不到位,抓紧复习。切忌盲目刷题,解决问题比机械练习更有效。
最后祝大家取得让自己满意的成绩,学到了知识,取得了进步就是最大的收获。











