IB数学高危玩家自救指南：拆解近3年真题规律 附7分学霸每日学习表

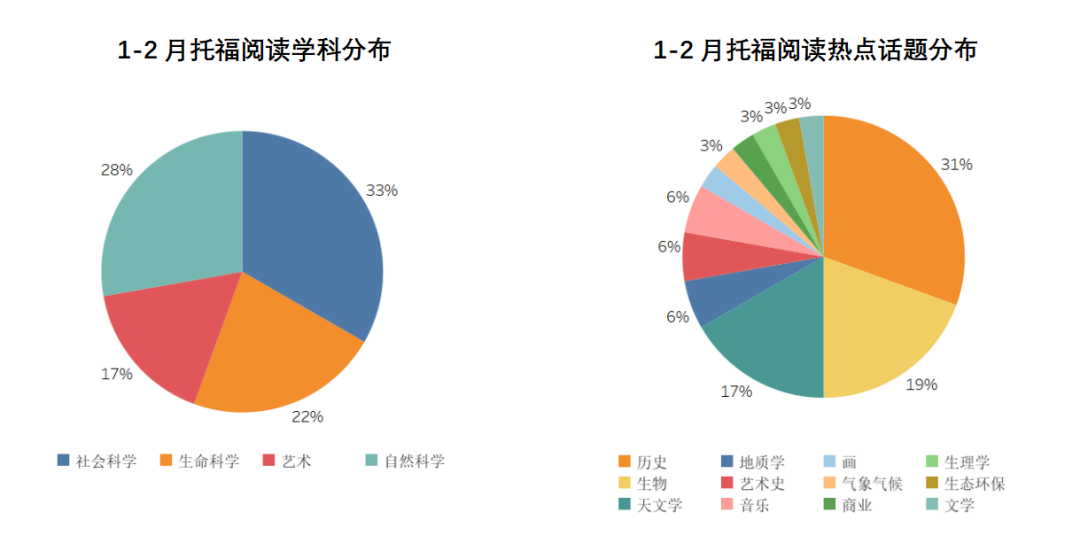
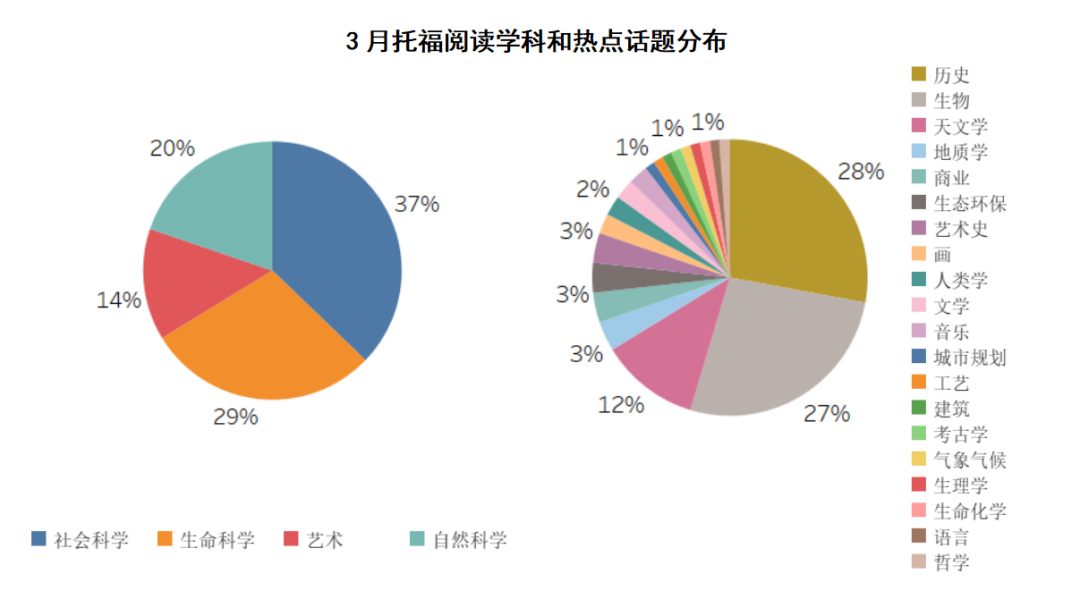
导语：

IB数学的7分率常年不足15%，但科学的规划与精准的突破能让成功率翻倍！举栗教育范老师基于300+高分学员案例，耗时3个月整理出这份全网最全攻略。

从课程本质认知到每日学习计划，从IA论文选题到考场时间分配——本文覆盖IB数学全生命周期管理，文末附50页高频考点手册+全真题库，建议搭配笔记本阅读！

一、IB数学本质解析：为什么它被称为“国际课程天花板”？

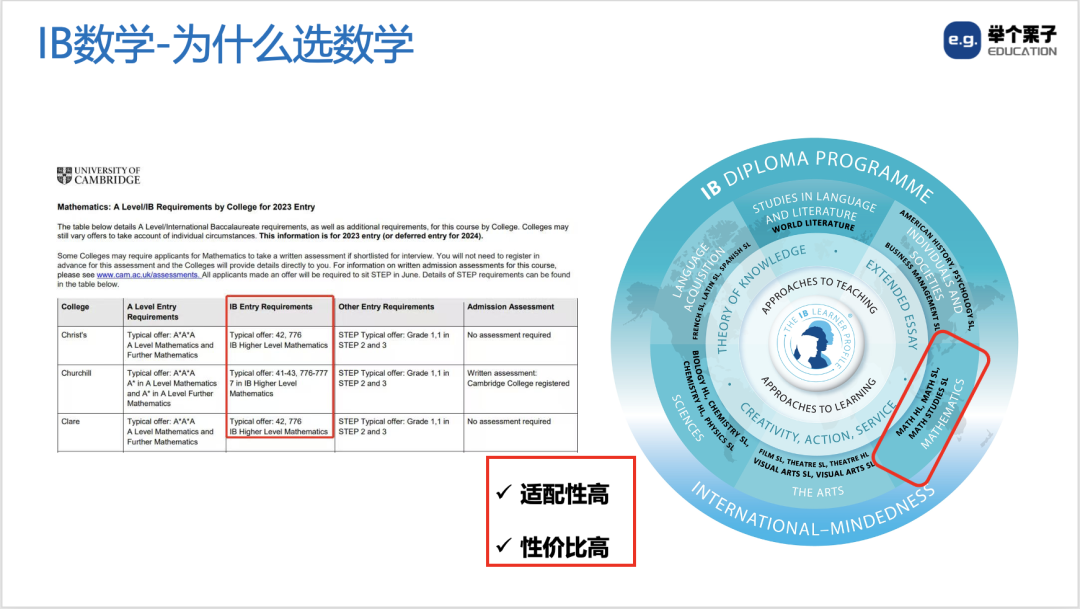
▲ IB数学在课程体系中的核心地位

1、课程设计底层逻辑

IB数学绝非知识点的简单堆砌，其核心在于跨学科整合能力+数学思维抽象化：

◉跨学科性：微积分用于经济学边际效益分析（AI方向）、向量与物理力学结合（AA方向）。

◉思维层级：从计算（Calculate）→ 应用（Apply）→ 探究（Investigate）的梯度跃升，HL Paper 3直接考察大学预科内容。

📃案例：2023年AA HL真题要求用微分方程模拟疫情传播（R0值计算+矩阵联立），本质是数学与生物学的交叉命题。

2、全球7分率数据透视

◉HL残酷现实：AA HL全球7分率仅9.2%，AI HL为11.7%（IBO 2023年报告）。

◉SL保分误区：AI SL看似简单，但因大量统计建模题，7分率反而低于AA SL（7.8% vs 8.5%）。

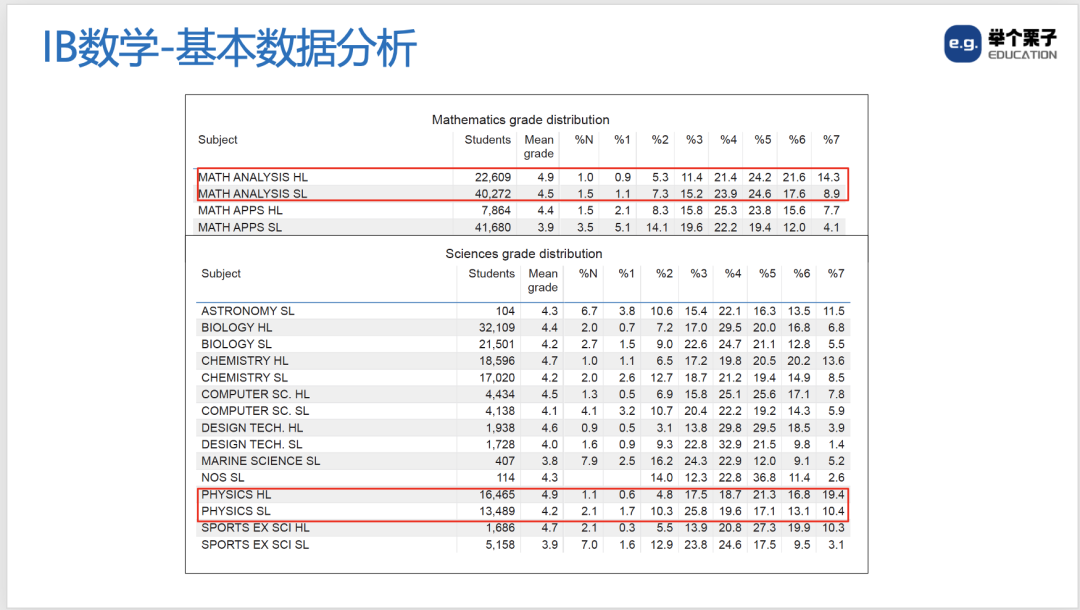
▲ 2023年IB数学各科目7分率对比（红色为HL，蓝色为SL）

二、IB数学四大模块全拆解：从知识地图到致命难点

模块1：代数与函数（占25%）

◉ AA方向核心：

➢ 递归数列通项公式（如an+1=2an+3an+1=2an+3，需掌握特征方程法）。

➢ 矩阵运算与几何变换（反射矩阵、旋转矩阵的复合应用）。

◉ AI方向重点：

➢ 线性回归模型的最小二乘法推导（Paper 2必考）。

➢ 逻辑回归的几率比（Odds Ratio）计算。

‼️ 高频陷阱：复数运算中i2=−1i2=−1的隐藏条件（如−4=2i−4=2i，但题目可能限定实数域）。

模块2：几何与三角（占20%）

◉ 三维几何必杀技：

➢ 向量叉乘求平面法向量。

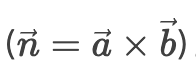
➢ 直线与平面交点计算（参数方程联立求解）。

◉HL专属难点：

➢ 极坐标下的积分求面积（如r=2(1+cos⁡θ)r=2(1+cosθ)围成的图形面积）。

📃真题示例：2022年AA HL Paper 2第10题——用向量法证明四面体体积公式（需结合混合积a⃗⋅(b⃗×c⃗)a⋅(b×c)）。

模块3：统计与概率（AI方向占35%）

◉泊松分布实战：

➢ 条件概率计算（如已知某店每小时客流量服从λ=5λ=5，求下一小时客人≤3的概率）。

➢ 拟合优度检验（Chi-square Test）的完整步骤（假设→期望频数→统计量→查表）。

‼️ 避坑指南：置信区间（Confidence Interval）的表述必须包含“总体参数”与“置信水平”（如“95% CI for population mean”）。

模块4：微积分（AA方向占40%）

◉微分方程高阶技巧：

➢ 分离变量法（如dydx=y(1−y)dxdy=y(1−y)的解为y=11+Ce−xy=1+Ce−x1）。

➢ 欧拉法数值解（HL需掌握误差分析）。

◉积分应用巅峰题：

➢ 旋转体体积计算（绕y轴旋转时需用壳层法：V=2π∫abx⋅f(x)dxV=2π∫abx⋅f(x)dx）。

➢ 弧长公式的灵活运用（如s=∫ab1+[f′(x)]2dxs=∫ab1+[f′(x)]2dx）。

三、IA论文：从选题到满分的12个关键步骤

1、选题的黄金法则

◉避雷清单：

❌ 纯理论证明（如费马大定理）。

❌ 数据不可获取的课题（如国家机密级经济数据）。

✅高分选题模板：

➢ “利用正态分布优化XX超市库存管理”。

➢ “基于马尔可夫链的足球比赛胜负预测模型”。

2、数据采集与工具

◉AI方向必备：

➢ 爬虫工具：Python+BeautifulSoup抓取公开数据集（如WHO健康数据）。

➢ 可视化：Tableau制作交互式图表（如热力图显示概率分布）。

◉AA方向推荐：

➢ GeoGebra动态演示微积分几何意义（如导数为切线斜率）。

➢ LaTeX排版数学符号（推荐Overleaf在线编辑器）。

3、评分标准拆解（满分24分）

◉个人参与（6分）：需体现独立探索（如记录试错过程：“尝试了3种积分方法后发现壳层法最简”）。

◉数学表达（6分）：公式推导需完整（如从F=maF=ma到微分方程md2xdt2=−kxmdt2d2x=−kx的逐步转化）。

◉反思深度（6分）：需批判性分析局限（如“模型未考虑季节性因素导致预测偏差15%”）。

四、真题实战：5类必考题型+满分模板

题型1：三角函数综合题（Paper 1高频）

◉解题模板：

➢ 利用恒等式化简（如sin⁡2x=1−cos⁡2x2sin2x=21−cos2x）。

➢ 换元法求极值（如设t=cos⁡xt=cosx转化为二次函数）。

➢ 验证定义域（如tan⁡xtanx在x=π2x=2π处无定义）。

📃2023年真题：求解2cos⁡2x+3sin⁡x=02cos2x+3sinx=0在[0,2π][0,2π]内的解（答案：x=7π6,11π6x=67π,611π）。

题型2：微积分建模题（Paper 2压轴）

◉标准流程：

➢ 建立微分方程（如人口增长模型dPdt=kP(1−PM)dtdP=kP(1−MP)）。

➢ 分离变量求通解（P(t)=M1+Ce−ktP(t)=1+Ce−ktM）。

➢ 利用初始条件定参（如P(0)=1000P(0)=1000代入求C）。

➢ 解释现实意义（如环境承载量M对增长曲线的影响）。

题型3：统计假设检验（AI HL必考）

◉ 八步答题法：

➢ 陈述原假设H0H0与备择假设H1H1（如H0H0：骰子公平；H1H1：骰子不公平）。

➢ 选择检验方法（卡方拟合优度检验）。

➢ 计算期望频数（Ei=n×piEi=n×pi）。

➢ 计算统计量χ2=∑(Oi−Ei)2Eiχ2=∑Ei(Oi−Ei)2。

➢ 确定自由度（df=k−1df=k−1）。

➢ 查表得临界值（如α=0.05α=0.05对应χcrit2χcrit2）。

➢ 比较统计量与临界值。

➢ 结论：“拒绝H0H0”或“无充分证据拒绝H0H0”。

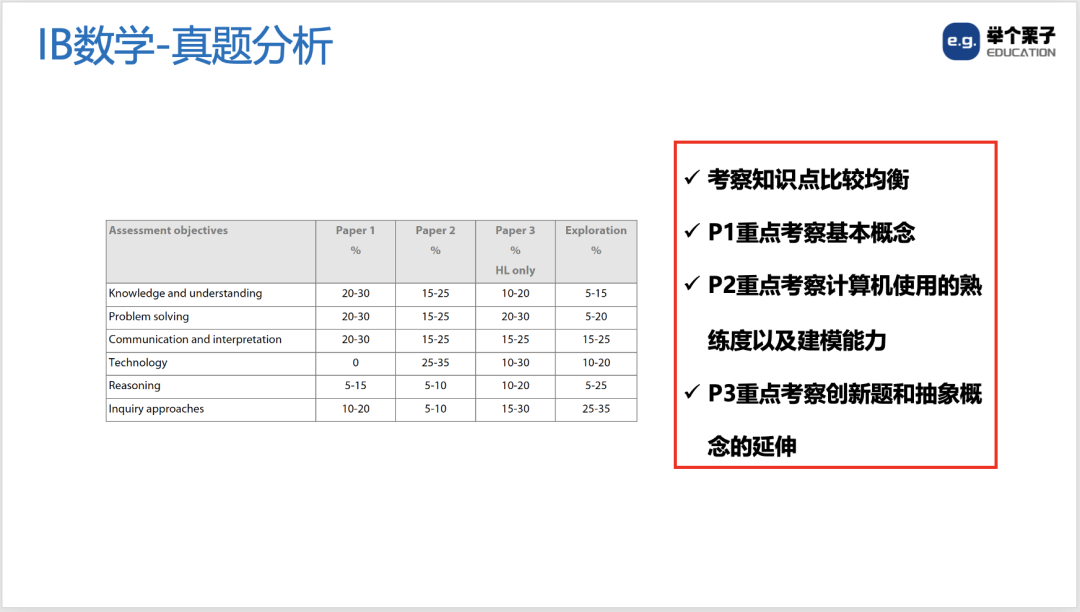
▲ IB大考需要的专业技能占比

五、从零到7分的365天计划表

十年级学生（Day 1-180）

◉晨间30分钟：

➢ 计算器快捷键训练（如卡西欧FX-991EX解方程：MODE → 5 → 1）。

➢ 背诵核心公式（如sin⁡(A±B)=sin⁡Acos⁡B±cos⁡Asin⁡Bsin(A±B)=sinAcosB±cosAsinB）。

◉晚间1小时：

➢ 完成教材章节练习（推荐牛津IB教材Chapter 1-4）。

➢ 错题归档至OneNote笔记本（分类标签：代数/几何/微积分）。

十一年级学生（Day 181-300）

◉周末攻坚：

➢ 周六上午：IA论文数据收集与清洗（用Excel剔除异常值）。

➢ 周日下午：HL专题突破（如向量叉乘的几何意义）。

◉模考节奏：

➢ 每月1次全真模考（限时+无外界干扰），成绩记录折线图。

十二年级学生（Day 301-365）

◉考前30天：

➢ 每日精做1套真题（2015-2023年），错题逐题录制讲解视频。

➢ 心理暗示训练：冥想+正念呼吸法（每天10分钟）。

六、资源库：7分选手的私藏工具箱

1、教材与题库

◉核心教材：

➢《牛津IB数学AA HL》（ISBN 978-0198427169）：例题经典，知识点串联清晰。

➢《Pearson Baccalaureate AI HL》（ISBN 978-0435193427）：统计建模案例丰富。

◉冲刺题库：

➢《IB Mathematics HL Worked Solutions》：含2010-2022年真题分步解析。

➢ 举栗教育独家《50个高频考点速查表》（文末免费领取）。

2、数字工具

◉思维导图：XMind绘制知识点网络（模板见下图）。

◉ 公式识别：Mathpix Snip一键转换手写公式为LaTeX代码。

◉ 错题管理：Anki设置每日复习提醒（按艾宾浩斯记忆曲线）。

▲ 向量章节思维导图模板（涵盖公式+题型+易错点）

结语：7分是系统工程的胜利

IB数学的难度本质是知识体系×时间管理×心理韧性的三维挑战。