IBAA (HL) Paper 1 难题解析

大家好，由我主讲的 IB AA（HL）大考冲刺班将于 4 月 7 日正式开启，用 7 节课，将 IB AA（HL）的知识点进行系统分类，辅以分类真题与答题思路，助你在考前洞悉所有难点、复杂点。

IB AA（HL）的考试一共由 Paper 1、2、3 三个部分组成，其中 Paper 1 和 Paper 2 卷面分值各 110 分，考试时长均为 2 小时; Paper 3 卷面分值 55 分，考试时长为 1 小时。

在 Paper 1 和 Paper 2 中 又各自细分为 section A 和 section B 两个部分。

Section A 题目分值较低，题目一般由 1 到 2 个小问题组成；

Section B 一共有 3 道大题，总分值在 50+ 到 60+ 之间，每道题目一般由至少 4 个小问题组成，是不折不扣的综合题。

Paper 1 和 2 同时占整个 IB 数学考试 40% 的分值比重，也需要我们在备考时重视这一部分的练习和知识点梳理。

虽说是综合题，但是每道题目基本还是围绕着课纲 5 个专题其中一到两个作为出发点进行展开。

今天我们首先来梳理一下 Topic 1：Number and Algebra 知识点相关的内容。

Topic 1 的主要内容包括多项式，二项式定理，复数，数列以及数学归纳法等相关证明。

其中，复数是在 Section B 出现比较高频率的一个专题。

因为复数这里本身包含的考察概念很多，例如三种不同形式 (Cartesian form, polar form, Euler's form) 之间的转换，又例如复数在复数平面的表示方法。

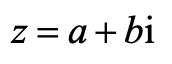
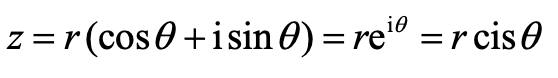
此外，复数部分还介绍了棣莫弗定理（De Moivre’s theorem），经常在复数根的求解使用。

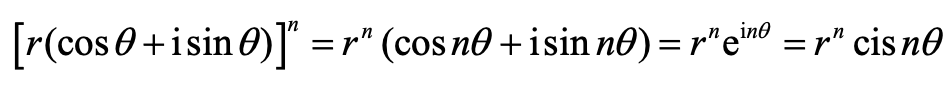
最重要的是，复数还可以和三角，多项式，几何相关知识结合进行考察。常见的形式有利用复数 Euler's form 推导三角恒等式：

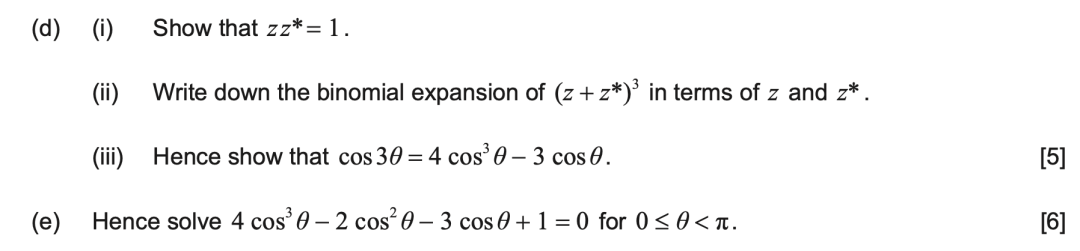
或者以复数根为出发点，求解多项式的相关问题。

又或者利用复数等式根在复数平面等分圆的特性，进行相关求解或者数学归纳法的证明。

除了复数以外，数列也是出现在 Section B 中作为主题干较长出现的一类题目。

在 Section B 的部分，经常出现以对数，指数，复数等其他形式出现的等差或者等比数列。本质上，还是需要掌握各种数列的一般形式和对应的求和公式。

等差数列：

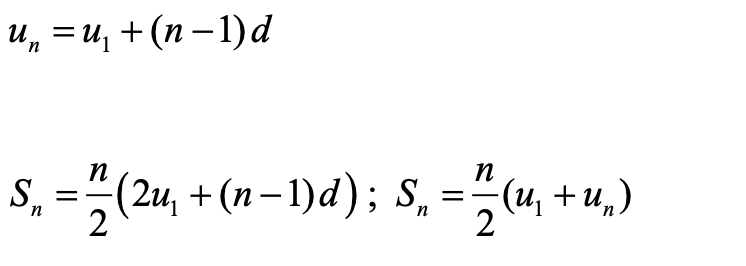
等比数列：

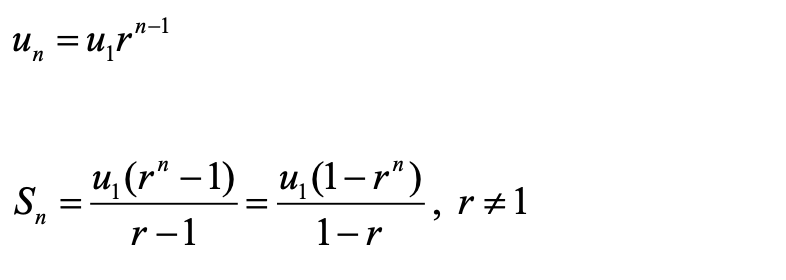
其中，等比数列又更为特殊，存在无穷项等比数列是否收敛的条件判定。这一内容经常和极限放在一起考察。

二项式定理和数学归纳法经常作为 Section B 某大题的一小问出现，关于二项式定理需要掌握常规的指数为正整数的展开公式，以及指数为任意数字的一般形式及其对应的展开条件。

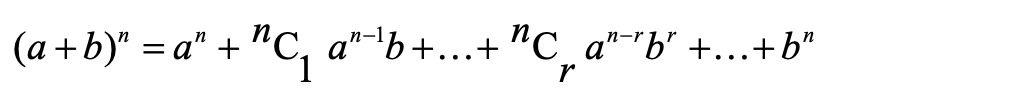
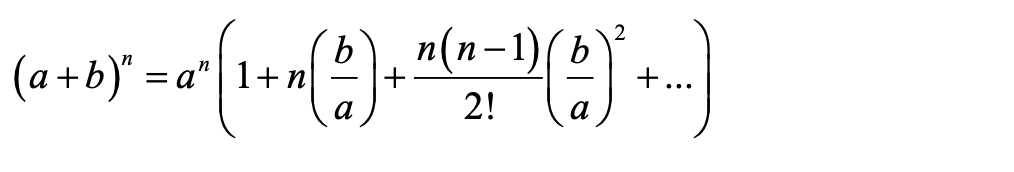
而数学归纳法，则是可以和一切内容“混搭”。最重要的是弄清楚其证明的主要三大步骤：

1 、证明初始值成立（多为 n= 1）；

2、假设 n = k 的时候命题成立；

3、将 n = k 的结果作为已知条件带入到 n =k+1 的命题中证明其成立。