IBAAHL 五个部分中的 Topic 2 主要包含和各类函数(funtions)相关的概念。是 Topic 1 (代数)到 Topic 4 (微积分)承上启下的一个部分。
在官方公式表中,Topic 2 给出的公式是最少的,且多与多项式(Polynomial)相关。但是实际上,函数部分的考察重点主要体现在函数的基本定义和不同函数的特性这两个大的方向上。
函数的基本定义主要考察包括定义域 (domain)、值域(range)、反函数(inverse functions)、渐近线(asymptotes)、复合函数(composite functions)以及奇偶性(odd/even functions)等内容。
同时又与微积分结合,考察函数的递增递减区间、驻点(stationary points)和拐点(point of inflection)。
课本上定义域和值域的定义:

另一方面,基于不同类型基本函数再加入函数变换,也让这一部分内容题型变得更多样化。
最常见的多项式函数(polynomial functions)问题中常出现找各轴交点,利用因式定理(factor theorem)因式分解等一些内容。有时还需要根据多项式的阶次,判断曲线左右两侧的趋势(end behavior)以及在 x 轴交点的特性。
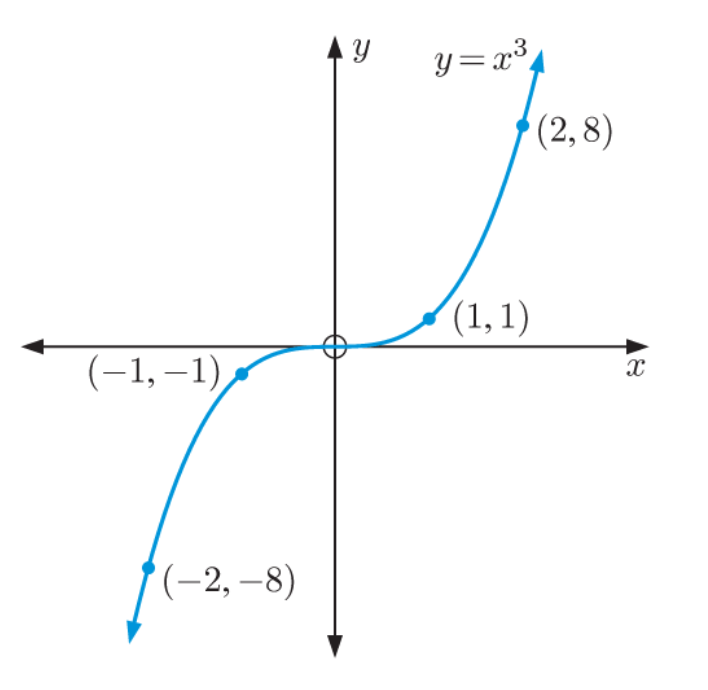
分式函数(rational functions)作为基于多项式函数的演化,在题目中常考察渐近线。
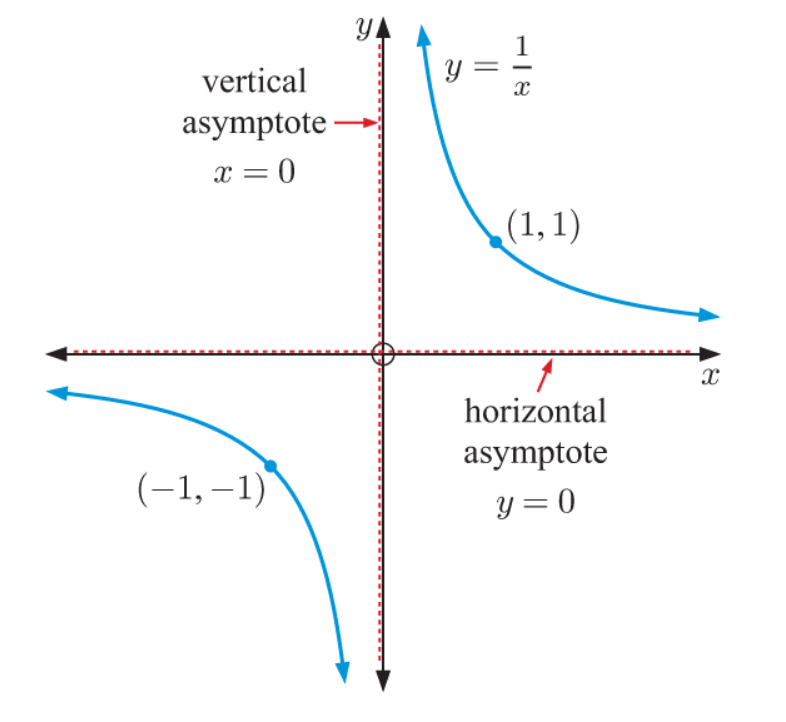
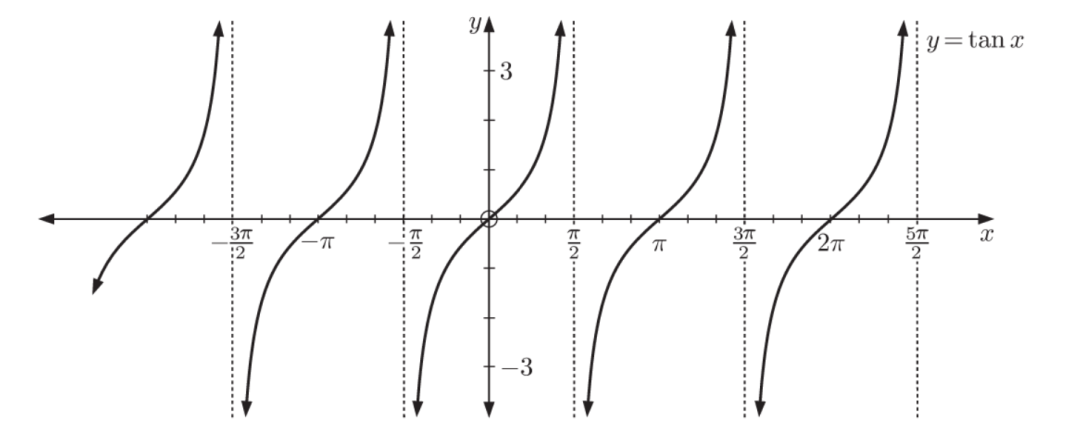
三角函数(trigonometric functions)的题目常出现振幅(amplitude)、周期(period)以及相位平移(phase shift)的内容。
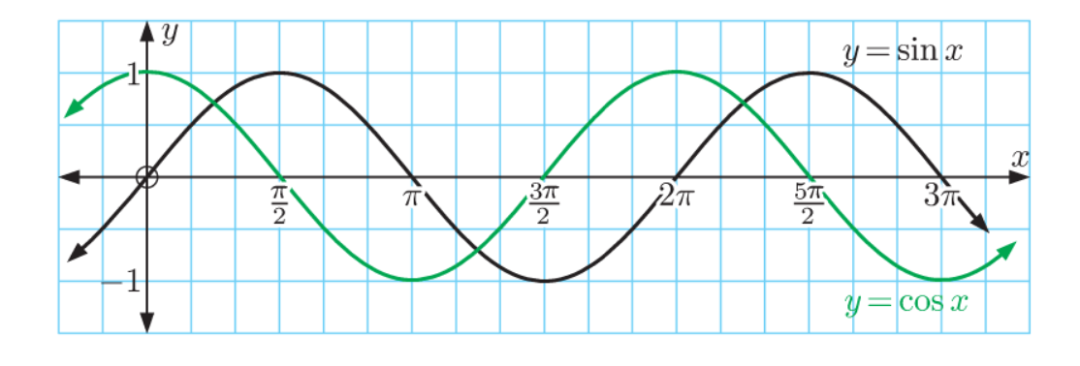
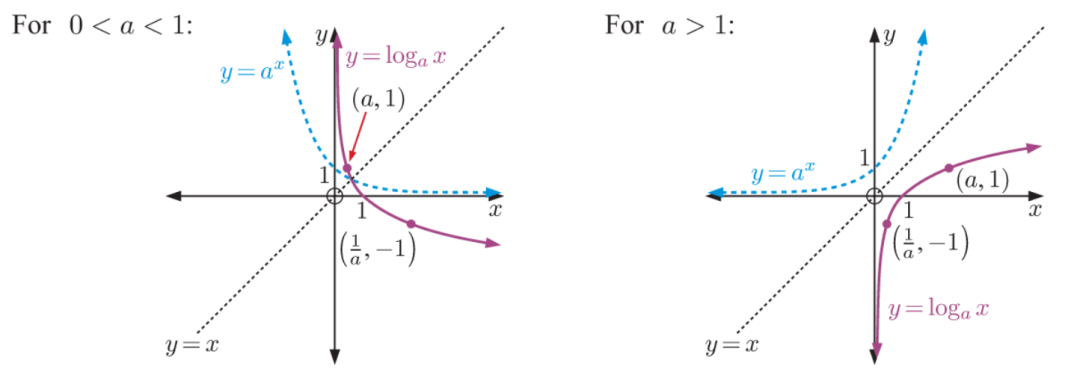
指数函数(exponential functions)和对数函数(logarithmic functions)常作为互为反函数的组合成对出现。
指数函数的考察方式包括复利的计算、指数的运算以及渐近线和非负性等。而对数函数经常涉及其非负的定义域,和与众不同的计算法则。
函数这个部分是一个非常倚重基础概念的部分,同时在基本概念之上的变形也比较多样。
因此,理清楚基本的表达式与图像是很重要的:
最后我们以一道往年的例题来看看 Topic2 在 Section B 出现的形式。

下面这道题中 a 小问全面考察了分式函数包括渐近线,定义域在内的主要特征并要求画图。同时也结合了微积分的部分内容,要求找出极大,极小值。
b) 小问主要考察了反函数的求解方法。
c) 小问则考察了复合函数。
不难看出,整个题目似乎想做到面面俱到,其实每一小问并不特别的难。