Topic 3：Geometry and Trigonometry 是 IB 考试中仅次于 Topic 5: Calculus 的大版块内容。
主要有两个考察的方向可以作为 Section B 中独立的大题。
重点知识点 1：三角
这一部分包含三角恒等式（trigonometric identities）,求解三角方程（solving trigonometric equations）,三角函数（trigonometric functions）等内容。
三角恒等式可以和复数一起考察，三角函数也可以和函数、微积分等一起考察。
要掌握好这个部分首先需要熟练记忆常用的三角恒等式。
也可以通过👇这个视频，了解一下 IBAA（HL）三角恒等式的真题：
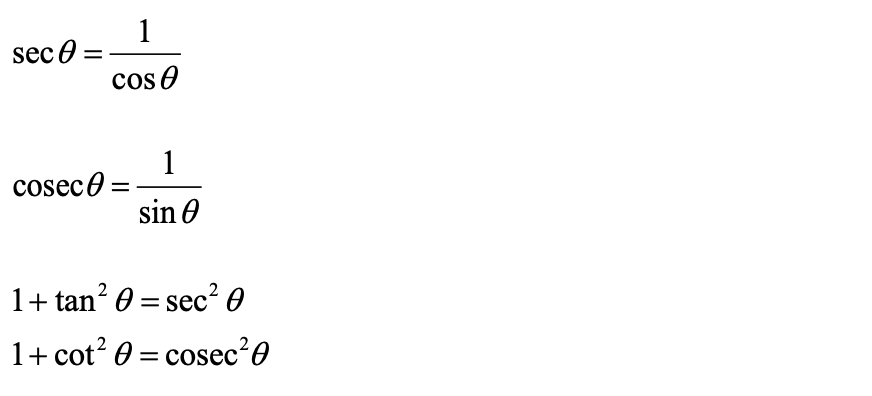
此外三角函数关于振幅（amplitude），周期（period）的定义也经常作为考察重点出现在小题中，又或者以应用题的形式出现。
（👇在考前看看三角函数的应用题真题）
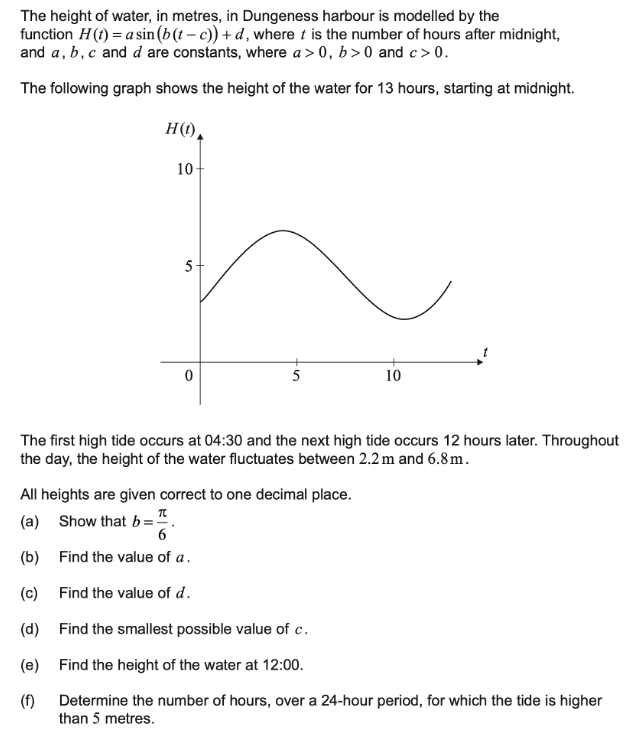
重点知识点 2：向量
第二个是向量（Vector）,主要涉及向量的定义、点乘（dot product/scalar product）和叉乘(cross product/vector product)计算的定义这些基本概念。主要考察方向包含向量与向量之间的关系，直线方程及相关应用，平面方程及相关应用。
点乘的考察，总是和求两个向量的夹角相关。当两个向量互相垂直时，它们的点乘结果等于零。
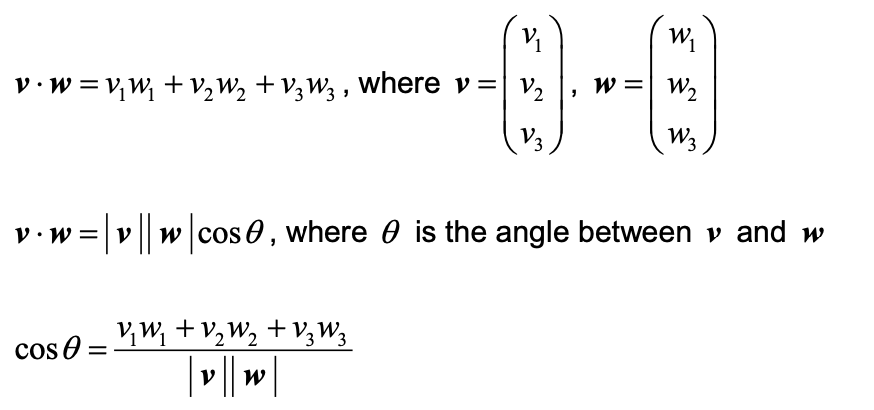
叉乘可以从两方面去理解，一方面叉乘得到的向量同时垂直于叉乘的两个向量，另一方面叉乘的大小代表叉乘的两个向量围成的平行四边形面积。
无论是直线还是平面方程，都可以通过一个向量，一个点来获得。直线的向量和直线平行。平面的向量和平面垂直。其中直线方程有三个形式，最有用的是“parametric form”可以用来求两条直线的交点，也可以用来求直线和平面的交点。
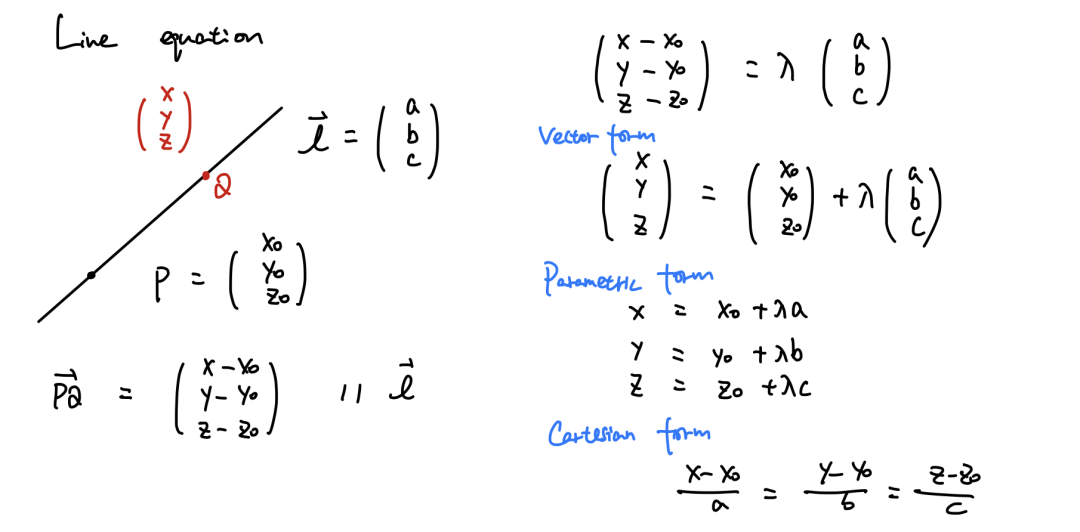
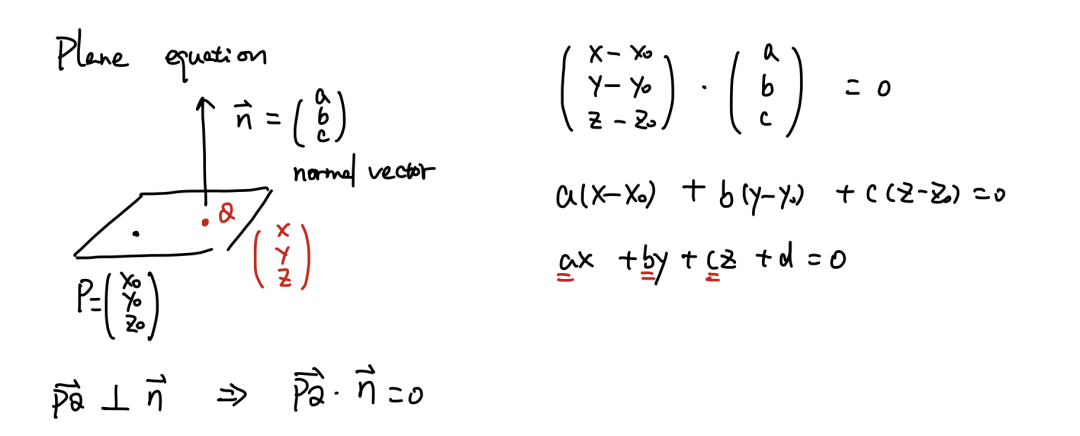
关于涉及直线和平面的问题，有很多可以“公式化”的求解过程。
例如求两个平面相交的直线，可以先求出和直线平行的向量，然后再求出过这条直线的某一个点。
求直线到面的距离可以先在直线上任意取一个点，然后利用和平面垂直的向量找到过该点与平面垂直直线的交点。
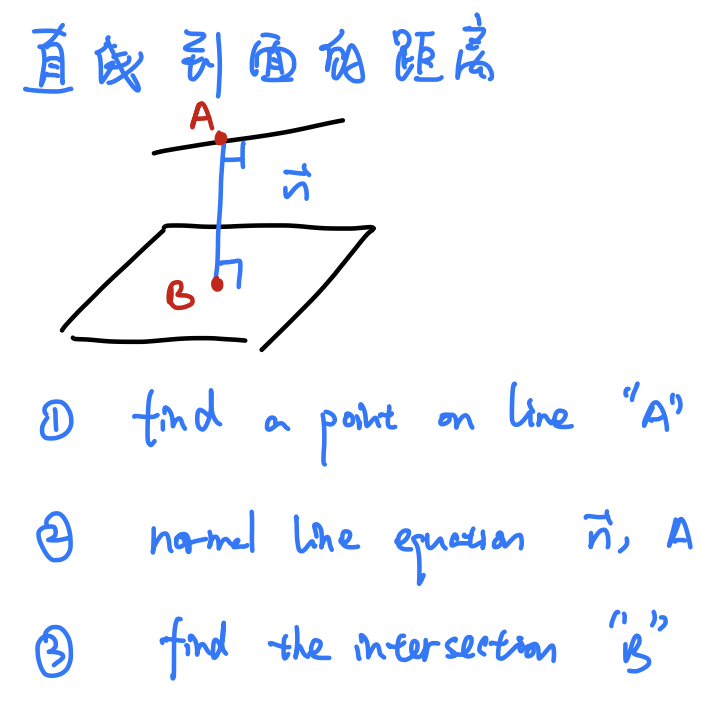
求直线和平面的夹角，实际就是求直线和平面垂直向量的夹角，然后再求直线与平面的夹角。
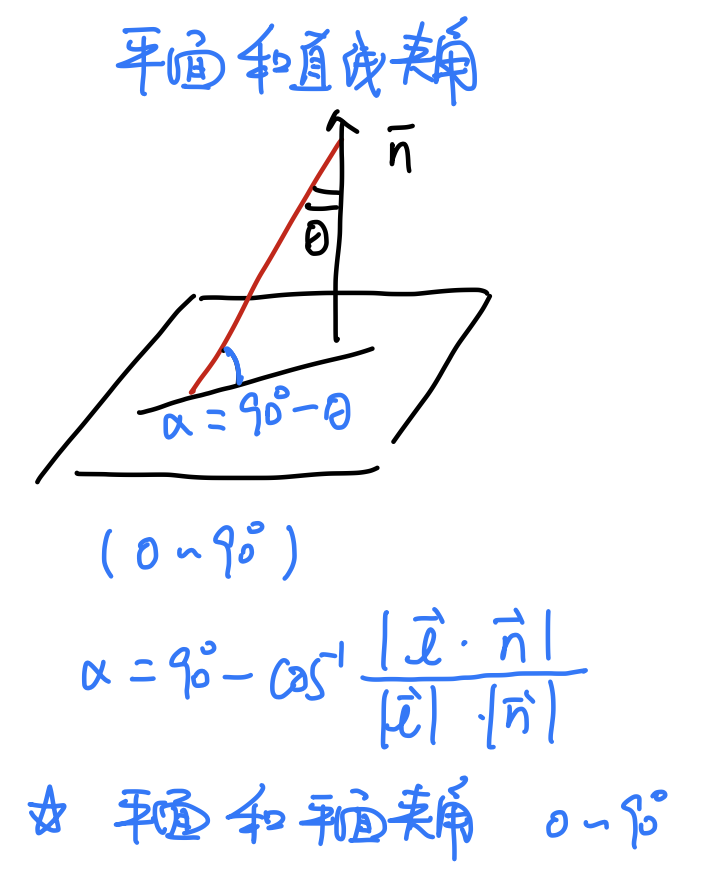
向量的部分包含的概念很多，想灵活应用一是需要理解每一个公式的推导过程，二是需要清晰每个和向量有关的问题实际需要求解的到底是点，向量，还是向量之间的夹角等。
【竞赛报名/项目咨询请加微信：mollywei007】
