IGCSE 数学学习学好这点拿 A* 不远！

大家好，今天说说英国的教育体制吧。

英国的教育体制经过数百年发展演化，将教育体系分为 5 个阶段（Key Stage，简称KS），其中家长熟知的 GCSE 处于第四阶段，也就是 KS4（Year 10-Year 11）。这个阶段，正是难度骤然上升的一个阶段。

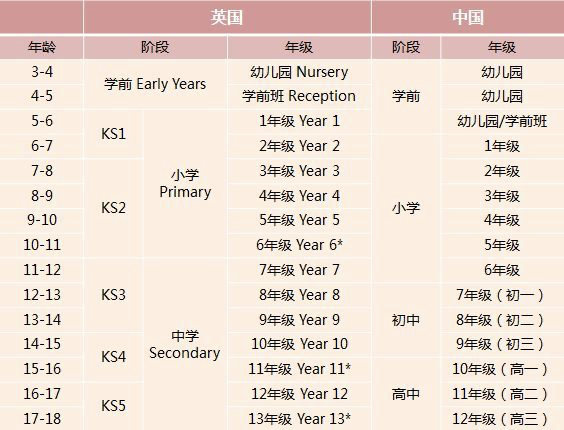
于是很多学生和家长在 KS3 数学步入 KS4 数学的时候会提出一个问题 —— 这个阶段需要做什么准备，才能让孩子更好的适应 KS4 阶段的学习。

其实大部分学校 KS3 和 KS4 阶段选用的教材在知识点上非常的契合，都是逐步递进，完全不需要什么特别补充的知识点。

那么跟着学校的节奏走就足够了吗？真的不需要做什么准备了吗？

其实不是的。虽然说知识点上不存在特别的缺口，但是数学的重点在于“逻辑推理能力”的培养。而这，正是 KS3 数学和过渡到 KS4 阶段的 IGCSE 数学最大差别。

IGCSE 数学相比 KS3 数学具体难在哪？

IGCSE 数学和 KS3 阶段相比，难度肯定是有所提升。那么具体难在了哪里呢？

在 KS3 中，我们学习了方程。但是仅仅局限于一元二次方程，简单的例子比如：

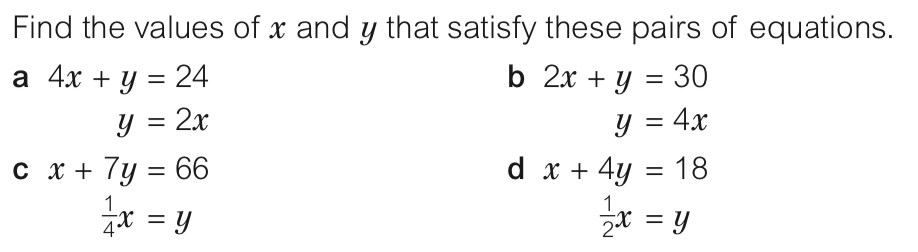
不难发现，KS3 数学的课程以基础知识为主，孩子可以不用考虑多种高难度知识点的配合使用，运用相对单一的知识解决相对单一的问题。比如，上图例子中，我只需要运用简单的代数的代入和加减乘除，就可以得到解答。

而进入到 IGCSE，同样的例子难度就上升到了新高度。

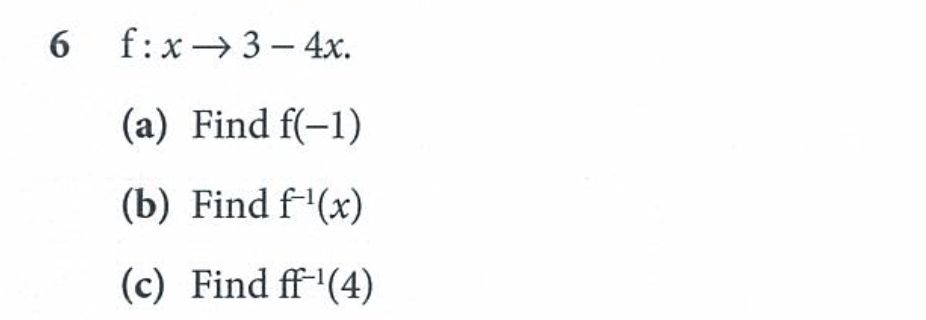
这样的难度升级对孩子们的要求变高了，比如在上图的函数中。体现如下：

首先，对于已经学会的知识的熟练程度 —— 如上图就涉及到了函数的意义、如何解方程、负指数的意义、分数的简化等等，孩子们必须在 KS3 阶段熟练掌握解决单一问题的能力。

其次，知识点们如何配合使用 —— 先解什么后解什么。这个其实就是“推理能力”。

在教研中，我发现 IGCSE 的难点其实是在这里 —— 当我们掌握的知识越来越多，如何将知识点组合起来，打出一套华丽的“组合拳”，反而变得不容易了！

在 KS3 数学中，如何解方程，如何简化负指数我们都学过了，但是变化成上图的函数后要怎么下手？

为什么知识学的越多反而不会用了？

其实这不是知识点的问题，而是思路的问题。在中国无论国际学校与否，很少有老师教你“逻辑”，这么一个概念。恰恰“逻辑”在学习中扮演者非常重要的角色。对于学生们来说，“逻辑推理”就是一个帮助他们去思考 —— 如何解决问题的工具。

当然，在 KS3 数学中知识简单且少的时候，我们不太需要强调这一点，因为问题往往都很单一，给你的已知条件也很明显直接。但是，进入到 IGCSE 涉及到运用学过的知识打组合拳的时候，“推理能力”的重要性就体现出来了。

我们看下面的例子：

首先，上图分为 KS3 和 IGCSE 两个阶段，同样的问题在不同的阶段的是正确答案不一样的。两个小红花分别代表了该阶段的正确答案。

注意看蓝色字部分，他们就是我们所使用的连招，由此对比可见 KS3 数学和 IGCSE 数学的差距非常的明显了，我们的“招数”多了，能得到的结果就更准确了。

而我们在 KS3 到 IGCSE 的过度期间，需要训练的就是如何使用连招。也就是上文所提到的 “逻辑推理”。

我们需要让孩子养成这种思维习惯，通过一步步的分析（正向或逆向思维），在自己的知识储备库里寻找出合适的“武器”，最后的到最优解。

以上图为例就是：

第一步，我们发现题目中分子分母的代数是不同的这样无法简化，那么我们需要把两个分数的代数一致化，所以我们需要先用到分数的乘法规则把所有代数汇聚到一起；

第二步，所有代数聚集到一起后，我们可以利用代数乘法规则换项；

第三步，换项后我们运用分数规则以及分数乘法规则，就可以做到分数代数一致化了；

第四步，我们分别运用分数中的指数规则，去简化两个分子分母一致化的分数；

第五步，我们发现其中含有 X 项的指数是负数，那么在简化过程中运用指数规则将指数的负号去掉，将此项变成带有正指数项的分数项；

第六步，将完全简化后的两项分数相乘，并运用分数规则得到 IGCSE 所要求的最优解。

以上六步的思考逻辑，就是我所说的 IGCSE 数学的难点 —— “逻辑推理”。孩子们需要在进入 IGCSE 阶段之前熟练掌握这项能力，以便于应付难度高的题目。