CJMC加拿大青少年数学竞赛详细介绍

CJMC简介：展现数学天赋初露

CJMC（Canadian Jay Mathematical Competition，加拿大青少年数学竞赛）由加拿大数学学会（CMS）主办，面向8年级及以下学生（对应英国及新西兰的9年级及以下）。这项竞赛不仅仅是一次考试，更是一个激发全球青少年数学热情、提升逻辑思维和解题能力的平台。与AMC8同级的CJMC，因其挑战性与创新性备受学术圈和教育界的认可。

为什么选择CJMC？

全球认可的权威竞赛：CJMC是加拿大数学学会举办的国际赛事，获得了全球教育体系的广泛认可，成绩突出的学生能够在学术圈中脱颖而出。

培养综合能力：竞赛涵盖了数论、代数、几何、组合数学及逻辑推理等多个数学领域，帮助学生在全面提升数学知识的同时，发展解决实际问题的能力。

展示数学天赋的绝佳机会：CJMC不仅为学生提供了展现数学才华的舞台，还可以作为未来竞赛进阶的基石。无论是未来参加CIMC、COMC，还是国际数学奥林匹克竞赛（IMO），CJMC都是一块坚实的跳板。

为申请世界名校增色：在申请大学时，数学竞赛成绩是学术成就的重要展示，CJMC的优异表现将为申请名校、尤其是理工科专业，增添一抹亮眼的光彩。

CJMC 2024考试基本信息

考试时间 (Date)：

日期：2024年11月23日，星期六，16:00-17:30

考试时长 (Duration)：90分钟

题目数量 (Number of Questions)：

共15个选择题，分为3个部分

每部分包含5道题

难度逐步递增，挑战学生的思维能力

奖项设置 (Awards)：

证书

所有正式参赛的学生都会获得一份证书，可以添加到他们的数学作品集中，或是装裱留作纪念。

未获得表现奖的学生（如上所述），根据成绩可获得“前四分之一”或“第二四分之一”的证书，未满足这些条件的将获得“参赛证书”。

获得表现奖的学生将获得注明其所获奖项的证书。

是否允许使用计算器 (Use of Calculators)：

不允许使用任何电子设备，包括计算器和电脑，旨在锻炼学生的手工计算能力和逻辑思维。

报名截止时间 (Deadline)：

2024年11月10日

竞赛内容概览

CJMC的题目涵盖广泛，挑战学生的各个数学领域技能。

以下为竞赛范围及部分例题示例：

数论 (Number Theory)

题目：Nicholas写下答案2023，狗Curly每次咬掉最后一位数字，依次得到202、20和2。要求将这四个数字相加，找出它们的和。

这道题目考查了数与数论的基础知识，尤其是数字的运算和基本的加法计算能力。题目中展示了逐步减少数字位数的操作，考生需要将不同位数的数字进行加法处理。这类题目不仅考查基本的加法技巧，还要求考生对问题中隐含的逻辑关系有敏锐的理解。

通过此题，学生可以加深以下能力：

数字的位数理解：理解逐步减少数字位数的概念。

基本加法运算：对不同位数的数字进行准确的加法计算。

逻辑推理：理清逐步操作中的数字变化关系，确保不会遗漏或出错。

这些技能在数论中非常基础，同时也是数学竞赛中常见的计算能力要求。

几何 (Geometry)

例题：

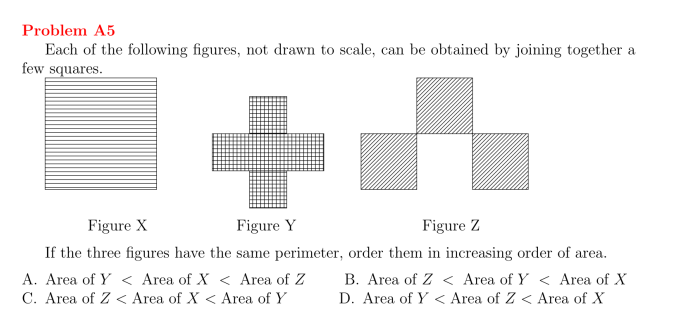
给出了三个图形Figure X、Y和Z，假设这三个图形的周长相同，要求按照面积从小到大的顺序排列。

这个问题与几何中的面积与周长关系紧密相关。通过这道题，学生能够深入理解以下几个几何概念：

规则性与面积的关系：对于相同周长的图形，越接近正方形或矩形的形状，其面积往往越大；而形状越不规则，面积则越小。

周长与面积的不同：虽然周长相同，但不同形状的图形包围的面积可能有很大差异。图形越接近规则多边形，其面积越大，这一点在几何优化问题中非常常见。

这类题目通过对图形的形状和面积的直观判断，训练了学生的几何直觉和逻辑推理能力。

组合数学 (Combinatorics)

例题：我们需要用$10钞票、$5钞票和$1硬币来支付$28。为了系统地解决这个问题，我们可以逐步考虑用不同数量的$10钞票的情况，来找出所有可能的组合方式。这道题通过考查学生对组合数学中不同面值货币组合方式的理解，培养他们对排列组合问题的解题思路。

逻辑推理 (Logic and Reasoning)

例题：

题目：有7个连续的整数，它们的和是2023。要求这些数的中位数是多少。

知识点：逻辑推理 (Logic and Reasoning)

这道题目考查的是连续整数的性质与中位数的概念。题目给出的线索是“7个连续整数”和它们的和为2023，解题思路是运用连续数的平均值与和的关系来求解。

注：添加行政老师获取真题及解析相关备考资料

为什么参加CJMC？

提高数学能力和逻辑思维 (Sharpen Mathematical and Logical Skills)参加CJMC不仅帮助学生通过解决高难度的数学问题来提高数学基础，同时也增强他们的逻辑推理和创新解题能力。

奠定未来高级竞赛的基础 (Prepare for Future Competitions)CJMC为学生进阶到如加拿大中级数学竞赛（CIMC）、加拿大数学奥林匹克（COMC）等更高级别赛事提供了重要的学习路径。通过CJMC，学生可以逐步提升，步步为营，迎接更高的挑战。

丰富大学申请背景 (Strengthen University Applications)作为国际知名的数学竞赛，CJMC的优秀成绩不仅是学术能力的证明，也是学生在申请大学时展示数学特长的有力凭证，尤其对申请理工科专业的学生极具竞争优势。

CJMC不仅是数学竞赛，它是学生个人发展的跳板，帮助他们在未来的学术和职业生涯中脱颖而出。