AMC8数学竞赛高频考点分析！建议收藏！

距今年AMC8数学竞赛还有三个月左右的准备时间，一定要抓住重点进行备考！首先复习高频考点，争取在同样的复习时间，获得更高的分数。

代数部分

1、比与比例、分数、百分比

通常有 3 至 6 题。比如涉及百分数、分数以及小数的多步骤计算、比较大小，以及它们在实际问题中的应用，像按比例分配、增长率等问题。学生要熟练掌握这些数的计算以及相互转化。

2、方程（包括应用题）

一般也有 3 至 6 题。包括一元一次方程、二元一次方程组等，常出现在行程问题、工程问题、利润问题等应用题中，要求学生能正确设未知数、列方程并求解。例如，根据路程 = 速度 × 时间的关系来列方程解决行程问题。

3、数列

有 1 至 2 题。可能考查等差数列、等比数列的通项公式、求和公式等，需要学生理解数列的概念和性质，能进行相关的计算和分析。

几何部分

1、三角形相似性、勾股定理

通常有 2 至 4 题。对于三角形相似，要掌握相似的判定条件和性质，能运用它们来证明线段成比例、求边长等；勾股定理则常用于求直角三角形的边长，以及判断三角形是否为直角三角形等问题。

2、圆形及其位置关系

有 1 至 3 题。涉及圆的基本性质，如半径、直径、周长、面积的计算，以及圆与直线、圆与圆的位置关系等。

3、四边形及其几何性质

会有 1 至 3 题。包括各种四边形（平行四边形、矩形、菱形、正方形等）的性质和判定，以及它们的周长、面积计算。

4、面积问题

在几何题中经常出现，要求学生能灵活运用等积变形、割补法等方法来求解不规则图形的面积，考验学生的空间想象能力和作图能力。

数论部分

1、质数（包括质因数分解）

一般有 1 至 3 题。学生要熟悉质数的概念、特征，掌握质因数分解的方法，能运用这些知识解决相关问题，比如求最大公约数、最小公倍数等。

2、整数、数位问题

有 1 至 3 题左右。例如，考查整数的性质、数位的意义，以及数的组成、分解等。

3、整除性

出现 1 至 3 题。常见的整除特征要熟练掌握，如能被 2、3、5、9 等数整除的数的特征，在判断数的整除性以及解决相关应用题时会用到。

组合部分

1、计数原理、排列与组合

有 2 至 4 题。涉及加法原理、乘法原理、排列数、组合数的计算和应用，在解决分组、分配、选取等问题时经常用到，需要学生理解原理并能正确运用公式进行计算，同时要注意区分排列与组合的不同情形。

2、概率（核心是计算）

有 1 至 3 题。包括古典概率的计算，如求简单事件的概率，以及对概率概念的理解和应用，可能与实际生活情境相结合。学生要掌握概率的基本计算方法和原理。

AMC8历年分数线

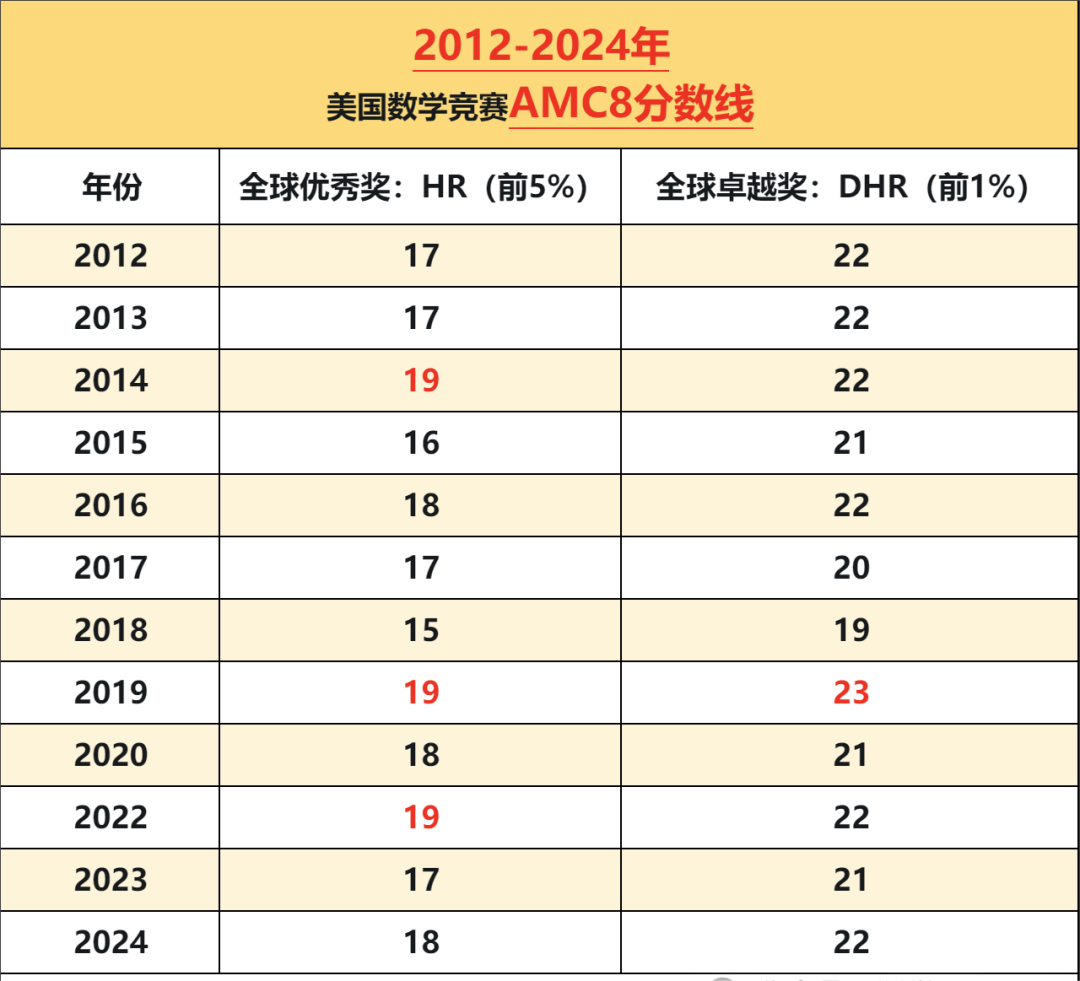
AMC8竞赛在考查内容上和国内教学大纲有90%的重合，学生转战AMC8难度不是特别大，只要数学基础扎实，经过系统训练，是非常有机会获奖的！