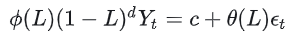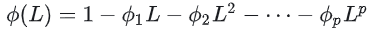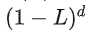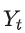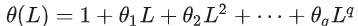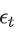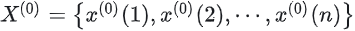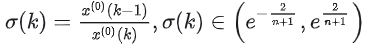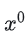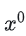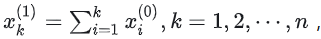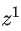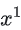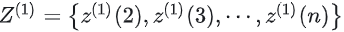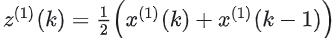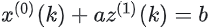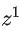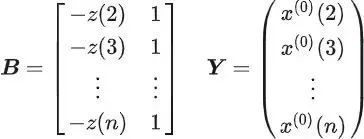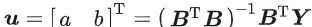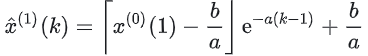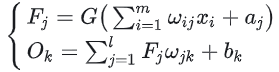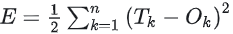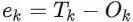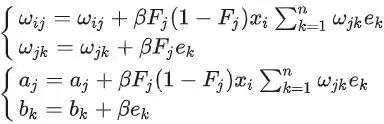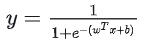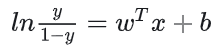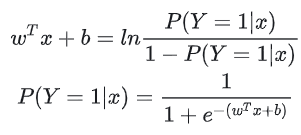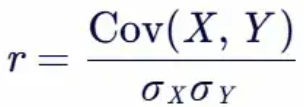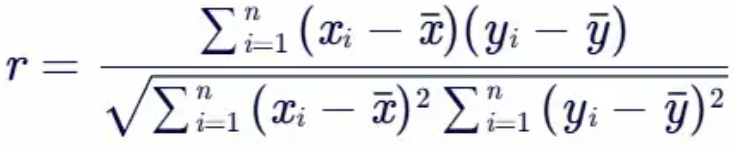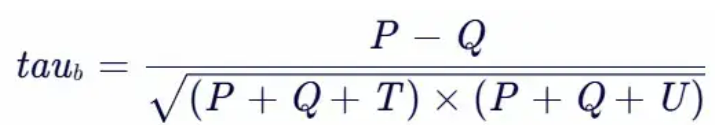2025国际数学建模竞赛IMMC冬季赛已经开启报名!想参加的同学们可以开始准备啦~
2024 IMMC比赛日程时间线
| 报名注册 | 秋季赛报名截止:
2024 年 11 月 21 日 冬季赛报名: 2024 年 11 月 25 日至 2025 年 1 月 22 日 |
| 秋季赛/
冬季赛 |
2024 年 11 月 21 晚 8 时至 11 月 25 日晚 8 时(秋季赛)
2025 年 1 月 22 日晚 8 时至 1 月 26 日晚 8 时(冬季赛) |
| 国际赛 | 2025 年 3 月 6 日晚 8 时至 3 月 11 日晚 8 时 |
| 答辩决赛 | 2025年4月下旬,香港 |
| 国际峰会 | 2025 年暑期,香港 |
要申请理工科专业的同学可以重点关注一下该竞赛,想要参加的同学也可以尽早咨询报名,合理规划学习时间!
还有不到半个月就要开赛啦!对于数据分析的新手小白,提升队伍竞争力的关键就是对模型有一定的掌握和了解,并且能够熟练地运用软件工具。今天将带领大家学习一下常见的模型!
数学建模模型大致可分为五类:
预测模型,评价模型,分类模型,优化模型,统计分析模型
本文将对预测模型、评价模型、分类模型、统计分析模型的一些常用算法模型的分析原理和软件操作进行详细介绍。
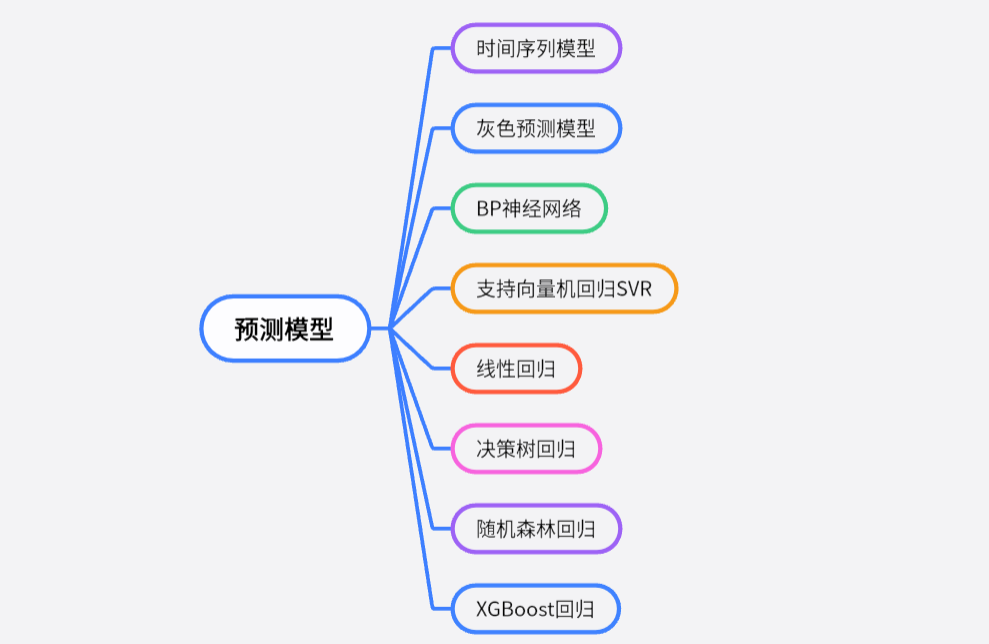
一、预测模型
预测模型是数学建模中利用数学、统计和算法,基于历史数据、趋势及外部因素,构建模型以预测未来现象、趋势或结果的工具。它广泛应用于经济、金融、市场、气象、环境等领域,旨在提供准确预测,辅助决策者制定有效策略。本文将详细介绍其中3种数学建模中常用的预测模型。
01、时间序列ARIMA模型
ARIMA模型,全称为自回归差分移动平均模型,是时间序列数据分析和预测的强大工具。它由自回归(AR)、差分(I)和移动平均(MA)三部分组成。ARIMA模型适用于平稳或非平稳但可转化为平稳的时间序列数据,能够捕捉长期趋势和季节性变化。
模型创新点
模型理论
ARIMA模型的一般形式为ARIMA(p, d, q),其中:
p:自回归项数,表示模型中使用的过去观测值的数量。
d:差分的阶数,表示为了使序列平稳而进行的差分次数。
q:移动平均项数,表示模型中用于预测误差的过去误差项的数量。
ARIMA(p, d, q)的公式可以表示
为:
是自回归多项式,L是滞后算子
表示对原始时间序列
进行d阶查分
是移动平均多项式
是白噪声序列
代表误差项c是常数项(在某些情况下可以为0)
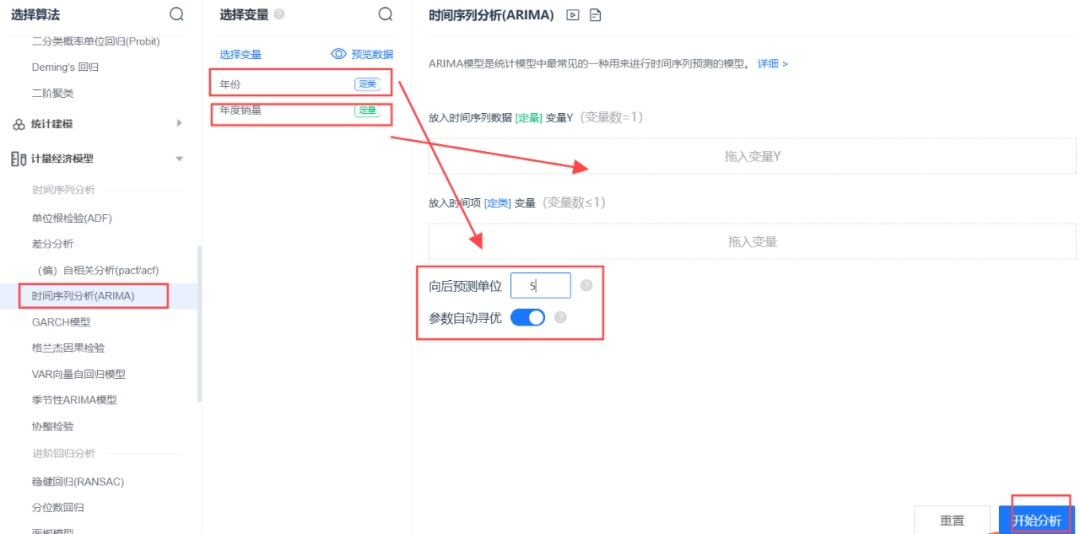
SPSSPRO软件操作
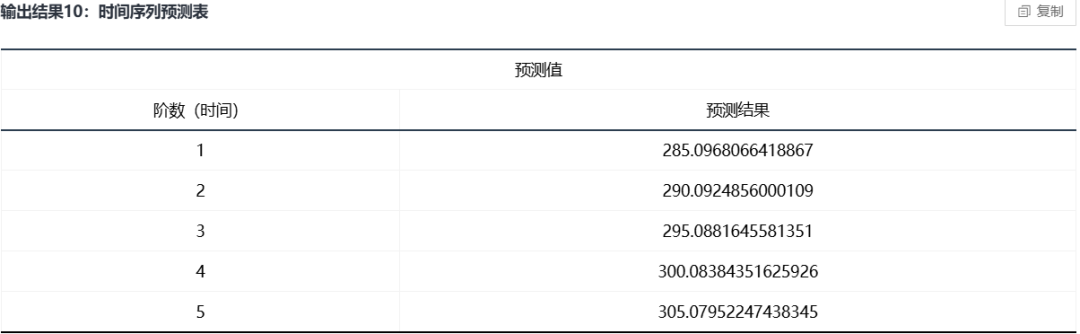
案例:基于 1985-2021 年某杂志的销售量,预测某商品的未来五年的销售量。
部分结果展示
02、灰色预测模型GM(1,1)
灰色预测模型GM(1,1)利用累加生成算子使数据具备指数规律,然后建立一阶微分方程求解,最后将结果累减还原得到预测值。该模型对数据要求不高,计算简便,适合短期预测,但对长期预测和非单调变化的数据序列效果较差。
模型理论
在建立灰色预测模型之前必须要保障建模方法的可行性,即需要对已知的原始数据进行级比检验 ,设初始非负数据序列为:
,只有当所有的 σ(k) 全部落入计算范围内才可以进行模型的建立。
级比的计算和判断公式分别为:
通过累加运算后得到的
一阶累加序列可以弱化
的扰动:
是
的紧邻均值生成的序列:
故可以求得 GM(1,1)模型对应微分方程为:
为GM(1,1)模型的背景值。
构建数据矩阵 B 及数据向量 Y ,分别为:
则灰色微分方程的最小二乘估计参数列满足
,其中,a主要控制系统发展态势,被称为发展系数;b的大小反映数据变化的关系,被称为灰色作用量。建立模型并求解生成值与还原值。依据公式求解, 可得到预测模型 :
经过累减,得到还原预测值。
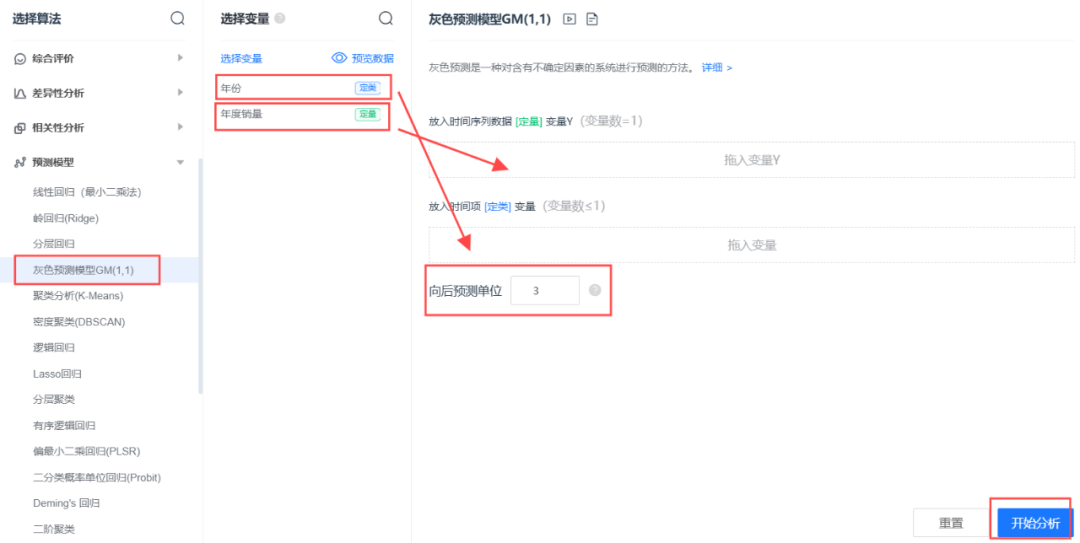
SPSSPRO软件实现
案例:基于某杂志 2006-2021 年某产品的年销售量,使用灰色预测模型对未来三年销售量进行预测。
部分结果展示:
03、BP神经网络
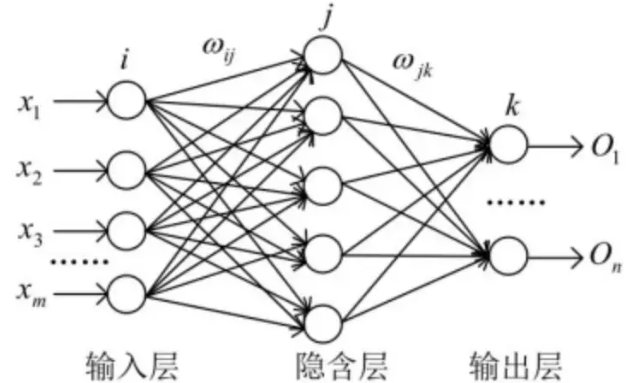
BP神经网络,即反向传播神经网络,是一种多层前馈神经网络。它由输入层、隐藏层和输出层组成,通过反向传播算法调整权重和偏置,以最小化预测误差。输入层接收数据,隐藏层进行复杂处理,输出层给出预测结果。BP神经网络能够处理非线性关系,具有强大的学习和适应能力,但也存在模型复杂度高、易陷入局部最优解等缺点。
模型理论
BP神经网络的核心是反向传播算法,该算法用于调整网络中的权重和偏置,以最小化预测误差。在训练过程中,网络首先根据输入数据前向传播得到预测结果,然后计算预测误差,接着利用梯度下降法等优化算法反向传播误差,更新网络中的权重和偏置,以减小误差。这个过程会不断迭代,直到达到预设的停止条件(如误差小于某个阈值、迭代次数达到上限等)。
以一个三层 BP 神经网络举例:
隐含层的输出量设为 Fj,输出层的输 m 量设为 Ok, 系统 的激励函数设为 G, 学习速率设为 β,则其三个层之间有如下数学关系:
系统期望的输出量设为 Tk,则系统的误差 E 可由 实际输出值和期望目标值的方差表示,具体关系表达式:
并令
利用梯度下降原理, 则系统权值和偏置的更新公式如下:
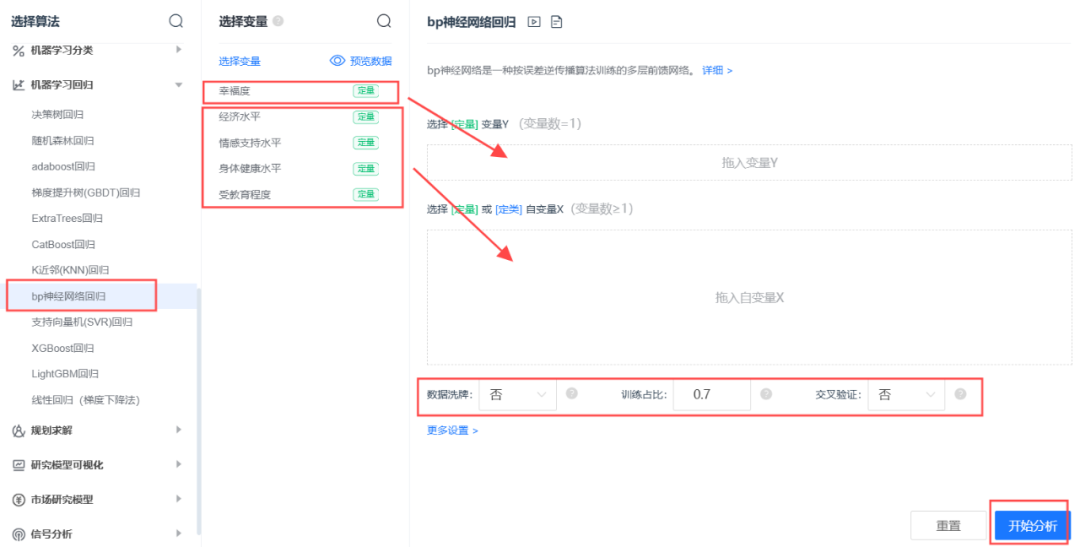
SPSSPRO软件实现
案例:研究“幸福感”的影响因素,有四个变量可能对幸福感有影响,他们分别是:经济收入、受教育程度、身体健康、情感支持。建立支持 bp 神经网络模型来预测幸福度。
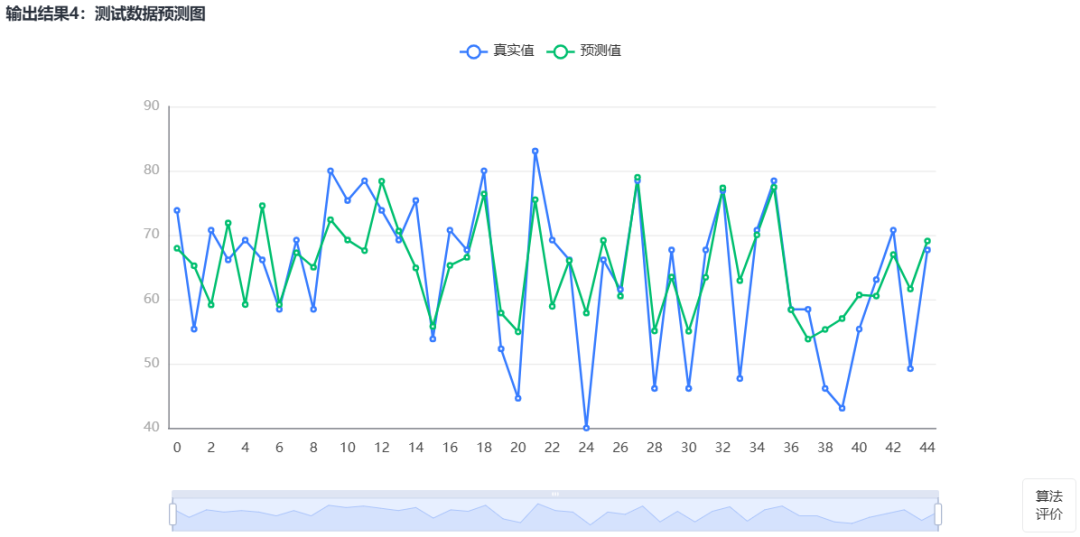
部分结果展示:
二、评价模型
评价模型是数学建模中用于对某个系统、方案或决策进行评估的数学工具,它结合了定性和定量的分析方法,通过构建评价指标体系、确定权重、计算得分等步骤,对评价对象进行综合评价,从而帮助决策者做出科学合理的选择。
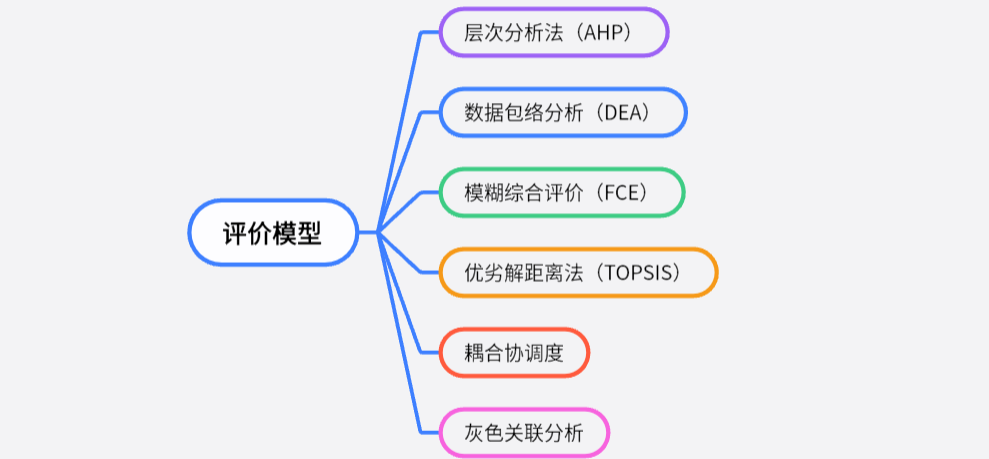
本节将详细介绍以下3种数学建模中常用的评价模型,包括:层次分析法(AHP)、模糊综合评价(FCE)、优劣解距离法(TOPSIS)
01、层次分析法(AHP)
ARIMA模型,全称为自回归差分移动平均模型,是时间序列数据分析和预测的强大工具。它由自回归(AR)、差分(I)和移动平均(MA)三部分组成。ARIMA模型适用于平稳或非平稳但可转化为平稳的时间序列数据,能够捕捉长期趋势和季节性变化。
模型原理
步骤 1:建立层次结构模型。
步骤 2:构造判断(成对比较)矩阵。
步骤 3:求解判断矩阵的特征向量。
步骤 4:对判断矩阵的一致性进行检验。
SPSSPRO软件实现
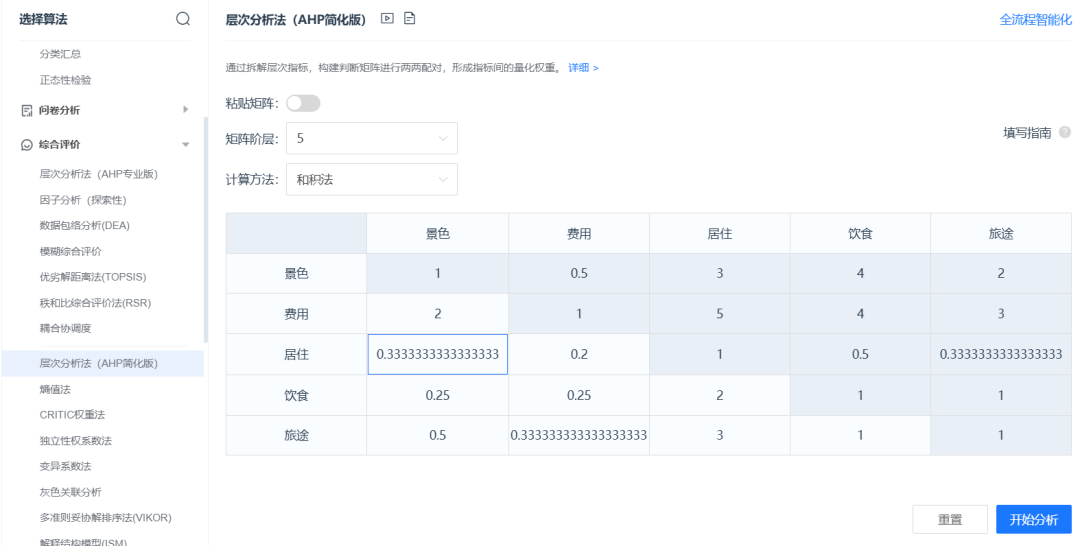
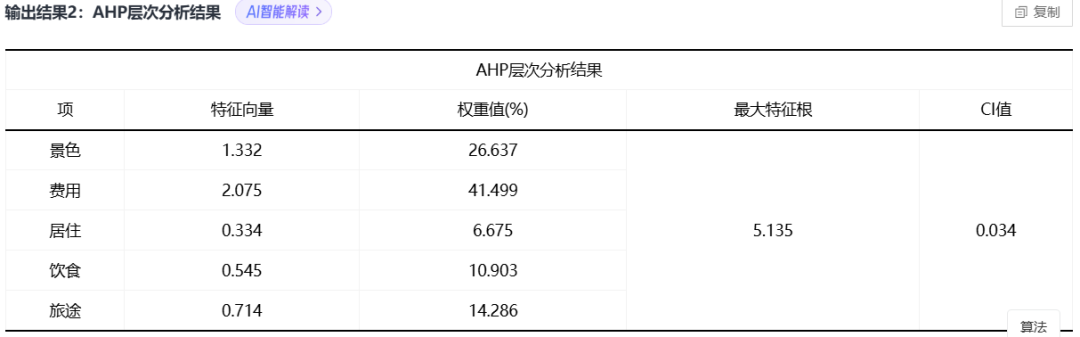
案例:通过构建评价指标(景色、费用,居住,饮食、旅途)对候选旅游地(桂林、黄山,北戴河)量化评价,进行选择。(这里层次分析法简化版主要针对评价指标(景色、费用,居住,饮食、旅途)的权重建立分析)
部分结果展示:
02、模糊综合评价(SCE)
模糊综合评价借助模糊数学的一些概念,对实际的综合评价问题提供评价,即模糊综合评价以模糊数学为基础,应用模糊关系合成原理,将一些边界不清、不易定量的因素定量化,进而进行综合性评价的一种方法。
模型理论
步骤1:明确评价因素集
步骤2:设定评语等级集
步骤3:构建模糊关系矩阵
步骤4:分配评价因素的权重
步骤5:实施模糊综合评价
SPSSPRO软件实现
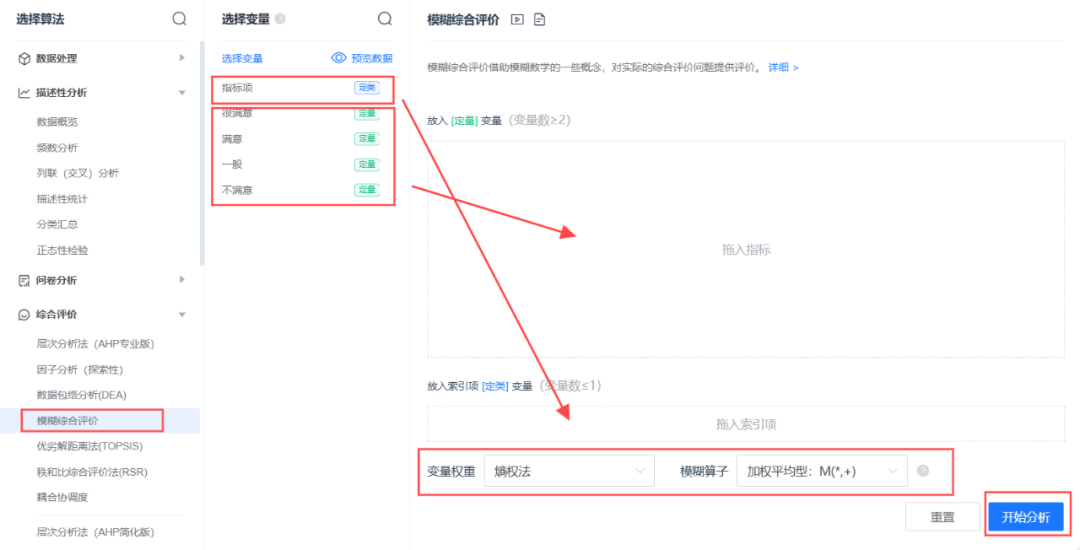
案例:某饮食行业品牌发布一款新零食,欲了解消费者对该种零食的接受程度。一共有五个评价指标(分别是价格、味道、包装、营养与性价比),以及评语共有四项(分别是很欢迎,欢迎,一般,不欢迎)。
部分结果展示:
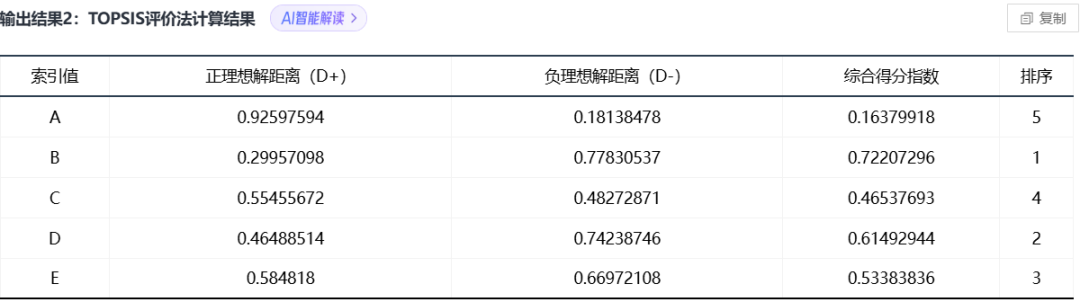
03、优劣解距离法(TOPSIS)
TOPSIS 法是一种常用的组内综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。
模型原理
步骤1:原始数据的正向化与趋势统一
步骤2:确定最优解与最劣解
步骤3:计算评价对象与最优、最劣解的距离
步骤4:评价对象与最优方案的接近程度
SPSSPRO软件实现
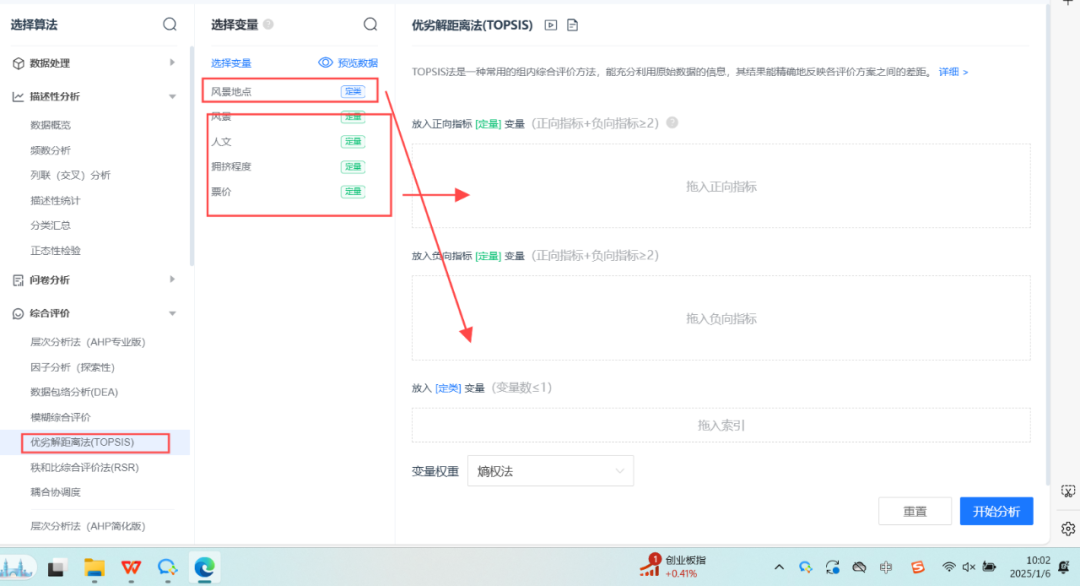
案例:为了客观地评价各风景地点的性价比,根据风景、人文、拥挤程度、票价等因素对各风景地点进行评估。
部分结果展示:
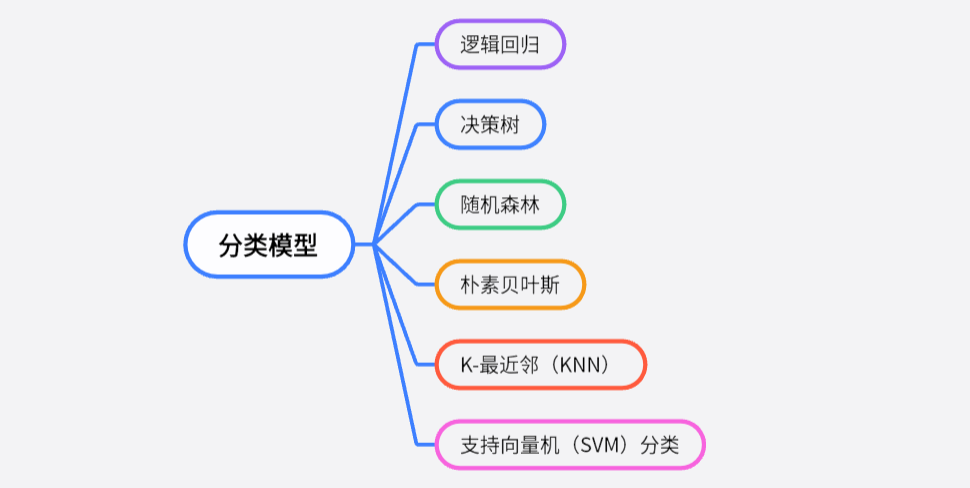
三、分类模型
分类模型是数学建模中一种根据数据特征将数据集中的实例划分为不同类别或组的模型。这些模型在机器学习、数据挖掘、统计分析等领域有着广泛的应用,能够解决许多实际问题。
01、逻辑回归
逻辑回归是一种线性回归分析模型,属于有监督学习的分类模型,主要用于二分类问题,即研究二分类因变量与一些影响因素之间关系的一种多变量分析方法,如果是多分类问题,则要用到多分类逻辑回归去研究因变量与一些影响因素之间的关系。逻辑回归直接建模分类可能性,无需假设数据分布,避免了假设分布不准确的问题。
模型原理
模型原理逻辑回归模型采用了对数几率函数(也称为sigmoid函数),该函数提供了一个平滑且可微的过渡,使得模型能够逐渐地从预测一个类别转变为预测另一个类
别:
即
其中, y 视为 x 为正例的概率, 1-y 为 x 为其反例的概率,两者的比值称为几率(odds),所以,逻辑回归中事实上因变量值应是 odds。将 y 视为类后验概率估计,重写公式有:
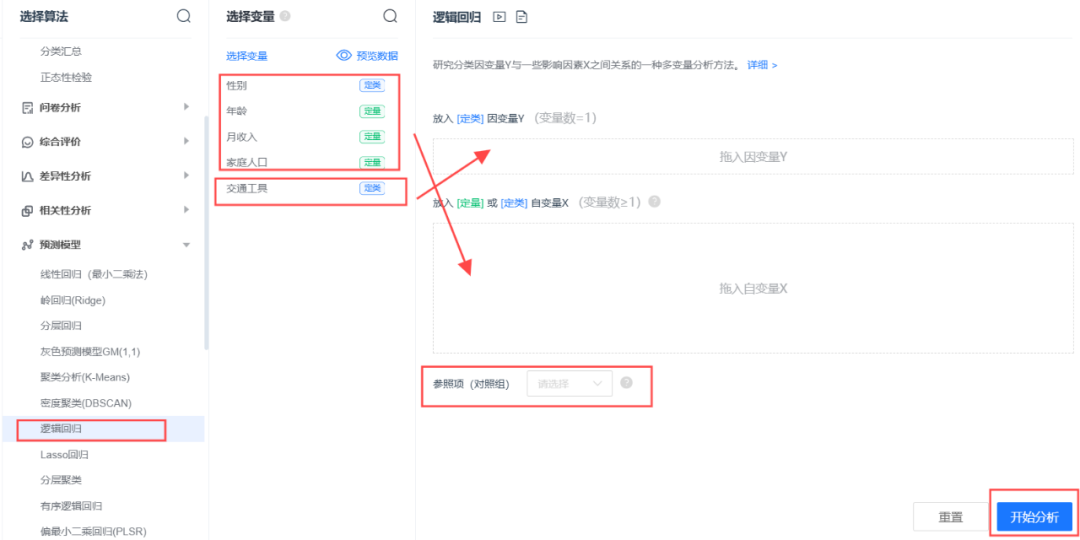
SPSSPRO软件实现
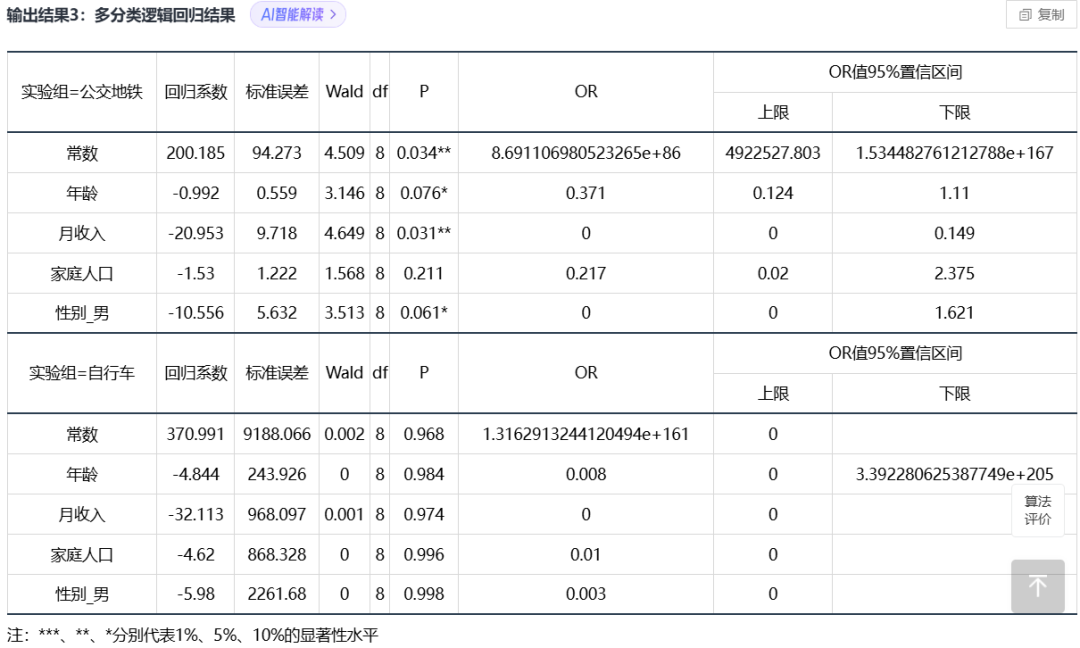
案例:根据年龄、月收入、性别、家庭人口等影响因素(自变量)来研究工薪群体的上下班交通工具是公交地铁、自行车、还是私家车(因变量)。
部分结果展示:
02、决策树
决策树就像一棵从根部长出的树,每个节点代表一个决策点,根据某个特征的取值将数据集分裂成不同的子集,这个过程一直进行下去,直到满足某个停止条件,每个叶节点代表了一个最终的分类结果。
在构建决策树时,通常会选择能够最大化信息增益的特征进行分裂,即选择那个能够使得分裂后的数据集“更纯净”(即同类样本更集中)的特征。熵是一个衡量数据集“纯净度”的指标,熵越小表示数据集越纯净。
模型理论
首先,从整个训练集出发,寻找最佳的初始分裂点,这一步骤涉及对所有潜在特征的评估,通过量化每个特征作为分裂标准的优劣,确定当前最优的分类指标。
随后,基于选定的最优特征进行数据集划分,并递归地在每个新生成的子集上重复上述过程,直至满足停止条件,如所有叶节点内的记录均属于同一类别。
之后,进行测试属性的选择。
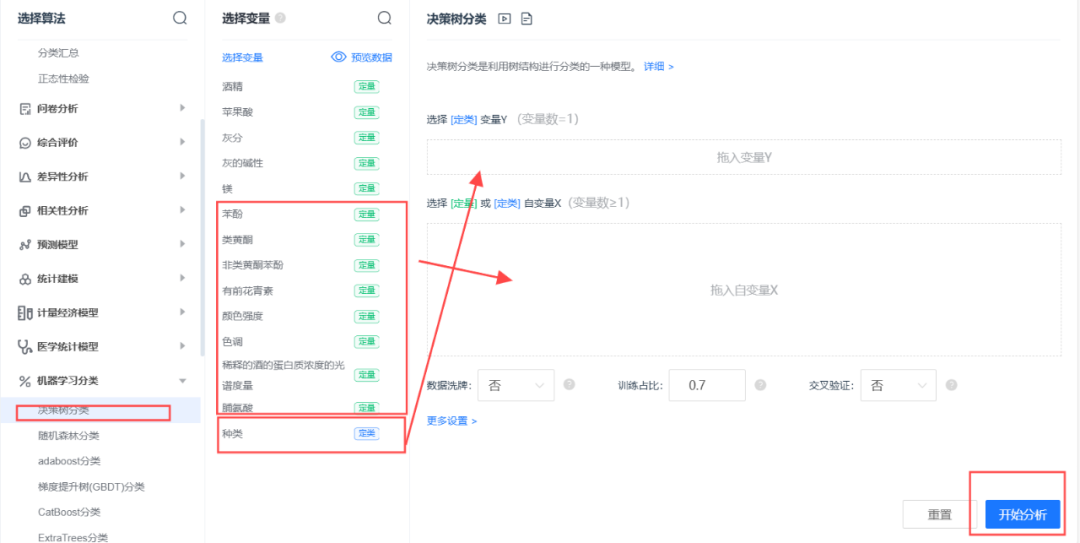
SPSSPRO软件实现
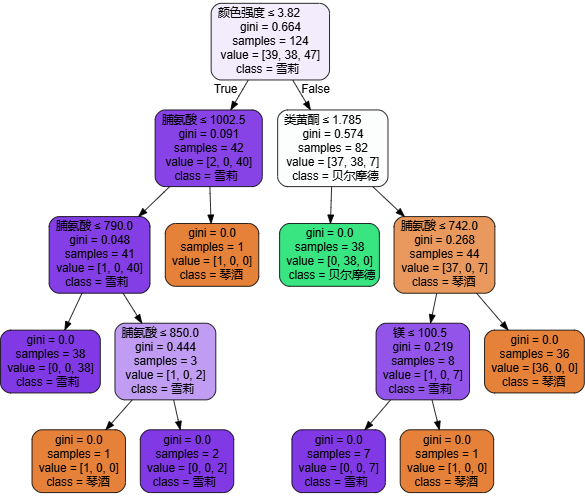
案例:根据红酒的颜色强度,苯酚,类黄酮等变量,生成一个能够区分琴酒,雪莉,贝尔摩德三种品种的红酒的决策树。
部分结果展示:
03、随机森林
随机森林是一种集成学习方法,它构建了多棵决策树,并通过汇总这些树的预测结果来进行分类。
每棵决策树都是独立构建的,并且它们之间没有直接的交互,在构建每棵树时,随机森林采用了装袋(Bagging)的策略,即通过有放回地随机抽样来生成训练集,使得每棵树的训练集都是不同的。此外,随机森林还在特征选择时引入了随机性,即在每个分裂点随机选择一部分特征进行考察,而不是考虑所有特征,这样做可以增加模型的多样性,从而提高整体的分类性能。
模型原理
步骤1:数据集准备与抽样
步骤2:决策树构建
步骤3:集成决策
步骤4:模型评估与选择
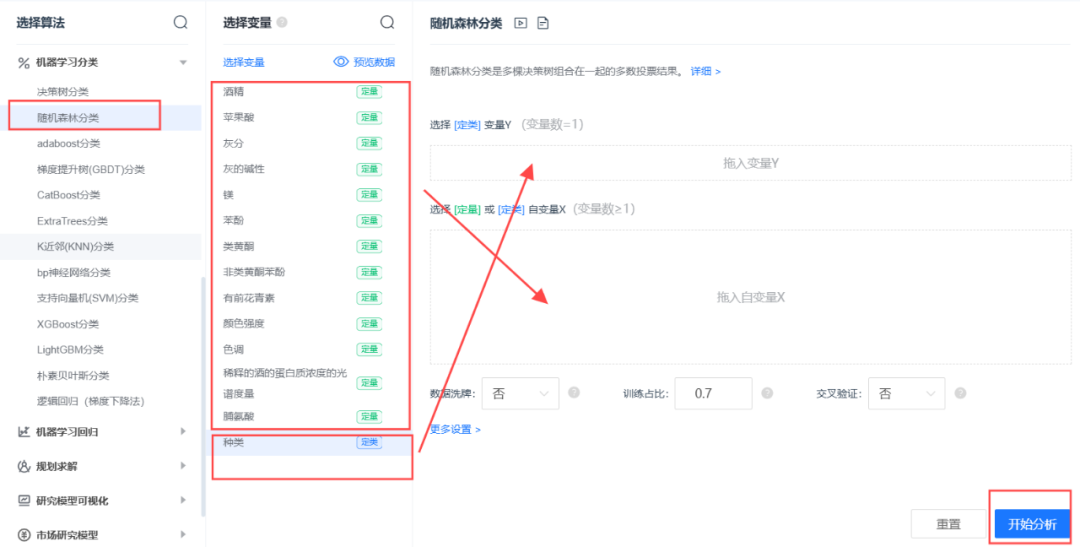
SPSSPRO软件实现
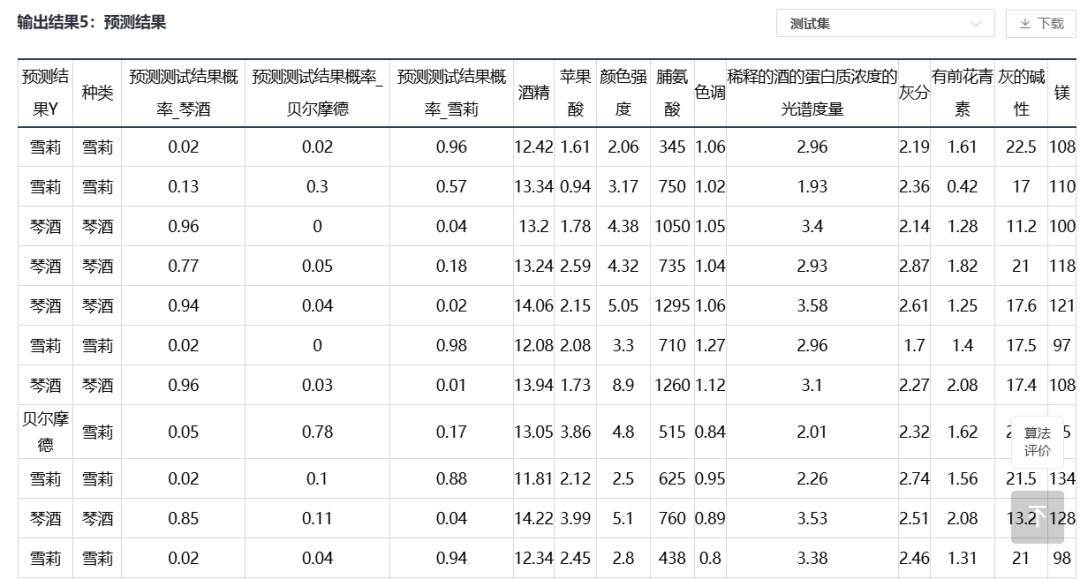
案例:根据红酒的颜色强度,脯氨酸,类黄酮等变量,生成一个能够区分琴酒,雪莉,贝尔摩德三种品种的红酒的随机森林。
部分结果展示:
四、分类模型
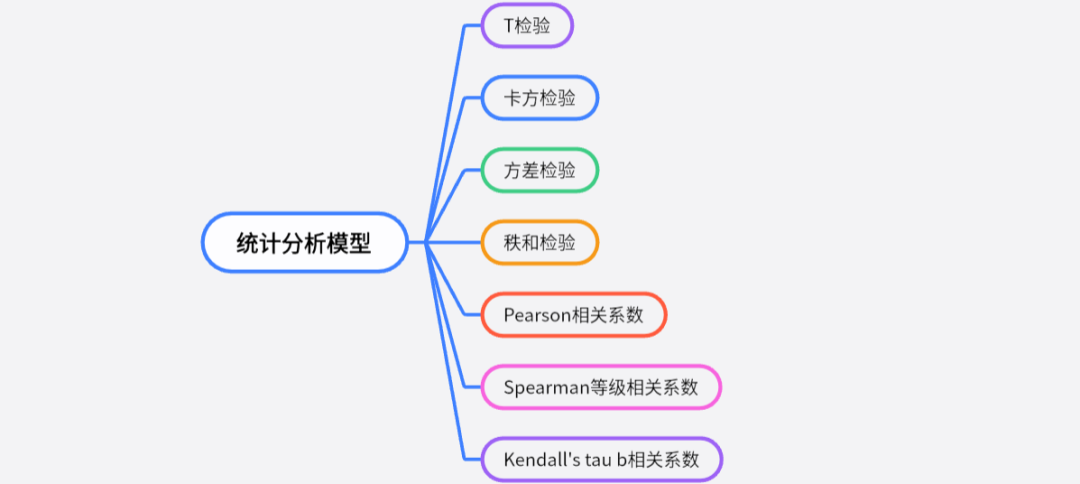
除了数学建模中常见的预测、评价、分类模型,还会涉及一些简单的统计分析方法,例如差异性分析、相关性分析、聚类分析等。常用的差异性分析方法主要包括参数检验和非参数检验两大类,常用的参数检验方法包括t检验和方差分析。常用的相关性分析方法有皮尔逊相关系数、斯皮尔曼等级相关系数和肯德尔等级相关系数等。
01、Pearson相关系数
Pearson相关系数是一种衡量两个连续变量之间线性相关程度的统计指标。它评估当一个变量发生变化时,另一个变量也随之发生变化的程度。取值范围在-1到+1之间,其中+1表示完全正相关,-1表示完全负相关,0表示没有线性相关。
模型原理
两个变量之间的Pearson相关系数定义为两个变量之间的协方差与它们各自标准差乘积的商。公式如下:
对于样本数据,我们使用 r 的样本估计值,通常用小写 r 表示:
其中,n 是样本大小,xi 和 yi 是样本观测值,xˉ 和 yˉ 分别是 X 和 Y 的样本均值。
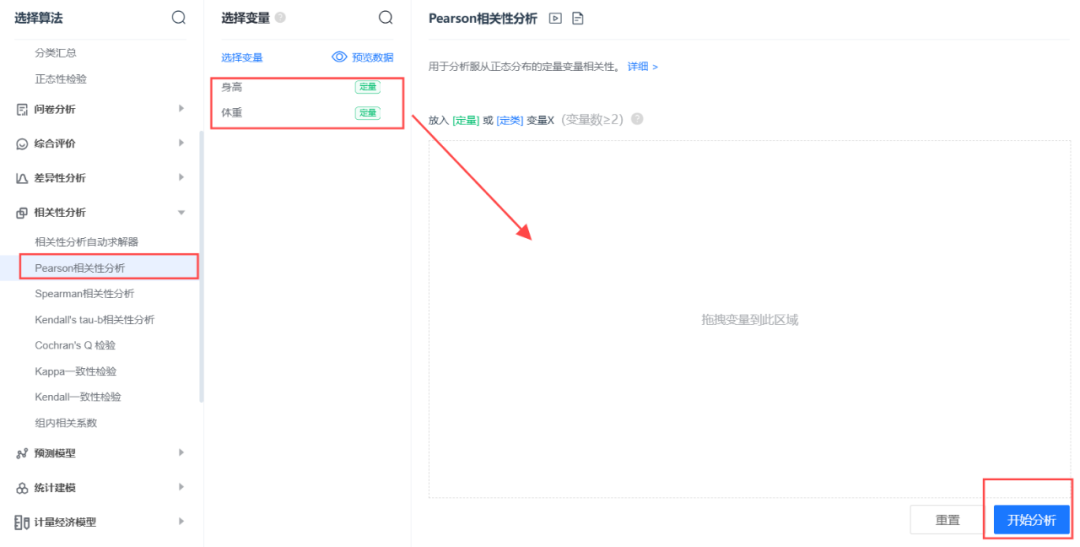
SPSSPRO软件实现
案例:人的身高和体重之间的相关性研究。
部分结果展示:
02、Spearman等级相关系数
Spearman等级相关系数是一种非参数统计方法,用于衡量两个变量之间等级或排名的相关性。它不需要变量数据服从正态分布,也不要求变量之间具有线性关系。
模型理论
1.对每个变量的观测值进行排序,并赋予等级(通常是排名,即第1小的为1,第2小的为2,依此类推)。
2.使用这些等级数据计算Pearson相关系数。
SPSSPRO软件实现
Spearman相关系数在SPSSPRO的操作方法与上述Pearson相关系数的操作相似,指定两个变量(连续或有序),系统将根据数据的等级排序计算相关系数并输出统计量,这里就不再赘述。
03、Kendall's tau b相关系数
Kendall等级相关系数是另一种用于评估两个有序变量之间相关性的非参数统计方法。与Spearman等级相关系数类似,但它更适用于处理存在结(即两个或多个观测值具有相同的等级)的情况。
模型原理
Kendall's tau-b 系数是用于反映两个有序分类变量相关性的指标。其计算公式为:
其中 P 是一致对的数量,Q 是不一致对的数量,T 是在 x 中但不在 y 中形成结的数量,U 是在 y 中但不在 x 中形成结的数量。如果 x 和 y 中有相同的分组且数量相同,则不计入 T 或 U。
SPSSPRO软件实现
Kendall's tau b相关系数在SPSSPRO的操作方法与上述Pearson相关系数的操作相似,指定两个有序变量,系统将根据数据的等级和是否存在结来计算相关系数并输出统计量,这里就不再赘述。