欧几里得数学竞赛,是加拿大滑铁卢大学(University of Waterloo)的数学学院为全球高中生举办的数学竞赛,有着“数学界托福”“AMC平替”之称,拥有超高的含金量和广泛的认可度,想要申请北美名校的同学必不可错过这项赛事!
2025年的欧几里得竞赛即将拉开帷幕,今天就让我们详细了解一下欧几里得竞赛的高频考点吧~
欧几里得竞赛高频考点
01、代数
代数部分约占30%的比例,主要考查学生的代数技能和解方程的能力。常见题型包括代数方程的求解、求函数的最大值或最小值、不等式的证明或解答等。熟悉一次函数和二次函数的图像,以及基本的代数操作,能大大提高答题效率。
02、几何
几何题目在竞赛中占有重要地位,约占总分的35%。这些题目通常要求计算面积或边长,同时证明面积分割、边长比例或大小关系等。
03、三角函数
三角恒等式和三角函数问题通常出现在第7至第9题,这类题目对于中国考生来说相对熟悉,他们能够较为顺利地解决。但一般情况下,如果出现了对数题目,就不太可能会再出现三角函数题目。
04、组合与概率
排列组合和概率是必考项目,通常分布在第5至第7题,有时也会在第10题与其他知识点结合进行考察。常见题型包括求排列或组合的个数、利用排列组合解决实际问题、概率计算等。
05、数论
数论题目在欧几里得数学竞赛出现的不多,常常是与计数结合,会放在第9或第10题。常见题型包括最大公约数与最小公倍数的求解、同余方程的求解、质数与合数的判定等。
06、函数
函数的定义及其性质是竞赛中的重要考点,包括反函数与复合函数的运用。
07、数列
数列及其求和也是考试中的常见考点,包括等差数列、等比数列的性质和求和公式。
08、解析几何
解析几何的应用是竞赛中的另一个重要考点,包括直线、圆锥曲线的方程和性质。
09、指数与对数函数
指数函数和对数函数的性质及其应用也是考试中的常见考点。
10、基础数论
基础数论包括质数与合数的识别、最大公约数与最小公倍数的计算方法。
11、组合学
组合学包括排列组合的基本原理和概率论的基础知识。
12、函数
函数的定义及其性质,包括反函数与复合函数的运用。
13、方程与方程组
方程与方程组的求解是竞赛中的基础考点,包括一次方程、二次方程和方程组的解法。
14、多项式
多项式的性质及其应用,包括二次、三次方程根的关系。
15、数列求和
数列求和的技巧,包括等差数列和等比数列的求和公式。
16、平面几何
平面几何的基本概念与定理,包括三角形、四边形和圆的性质。
17、面积和边长的计算
面积和边长的计算技巧,包括三角形、四边形和圆的面积和边长的计算方法。
18、三角函数的定义及性质
三角函数的定义及性质,包括正弦、余弦和正切函数的图像和性质。
19、三角恒等式的应用
三角恒等式的应用,包括和差化积、积化和差等公式。
20、排列组合的基本原理
排列组合的基本原理,包括排列数和组合数的计算方法。
21、概率论的基础知识
概率论的基础知识,包括概率的定义、计算方法和应用。
22、函数的定义及其性质
函数的定义及其性质,包括函数的图像、定义域和值域。
23、反函数与复合函数的运用
反函数与复合函数的运用,包括反函数的定义和复合函数的计算方法。
24、指数函数和对数函数
指数函数和对数函数的性质及其应用,包括指数函数和对数函数的图像和性质。
25、数列及其求和
数列及其求和的技巧,包括等差数列和等比数列的求和公式。
26、多项式及相关性质
多项式及相关性质,包括二次、三次方程根的关系。
27、方程组的求解
方程组的求解,包括一次方程组和二次方程组的解法。
28、平面几何的基本概念与定理
平面几何的基本概念与定理,包括三角形、四边形和圆的性质。
29、解析几何的应用
解析几何的应用,包括直线、圆锥曲线的方程和性质。
30、面积和边长的计算技巧
面积和边长的计算技巧,包括三角形、四边形和圆的面积和边长的计算方法。
31、三角函数的定义及性质
三角函数的定义及性质,包括正弦、余弦和正切函数的图像和性质。
32、三角恒等式的应用
三角恒等式的应用,包括和差化积、积化和差等公式。
33、排列组合的基本原理
排列组合的基本原理,包括排列数和组合数的计算方法。
34、概率论的基础知识
概率论的基础知识,包括概率的定义、计算方法和应用。
35、函数的定义及其性质
函数的定义及其性质,包括函数的图像、定义域和值域。
36、反函数与复合函数的运用
反函数与复合函数的运用,包括反函数的定义和复合函数的计算方法。
37、指数函数和对数函数
指数函数和对数函数的性质及其应用,包括指数函数和对数函数的图像和性质。
38、数列及其求和
数列及其求和的技巧,包括等差数列和等比数列的求和公式。
39、多项式及相关性质
多项式及相关性质,包括二次、三次方程根的关系。
40、方程组的求解
方程组的求解,包括一次方程组和二次方程组的解法。
欧几里得数学竞赛 比赛设置

面向学生:
任意年级高中生
比赛时间:
北美地区:2025 年 4 月 2 日
非北美地区:2025 年 4 月 3 日
报名截止日期:
2025 年 3 月 6 日
报名方式:
学生不能直接报名比赛,欧几里得不接受个人报名,若学校是考点,可联系自己班级的数学老师由学校统一报名。
需要先由学校教师向滑铁卢大学申请CEMC学校帐户,然后为学生预购比赛。学校帐户不会自动创建,提价申请之后,可能需要大约3周才能审查完毕。
如若学校不提供资源,可以给滑大官方发邮件询问具体参加方式,赛事组委会将会给学生分配在就近的考场参赛。
奖项设置:
个人奖项
🏅Certificate of Distinction:
在全球参赛者中排名前25%的学生均可获得证书
🏅Contest Medal:
由CEMC颁发给每个学校的冠军
🏅Honour Rolls:
分加拿大地区正式,加拿大地区非正式以及国际区域的高分参赛选手会被分别在各区域荣誉榜提名
🏅Plaque:
前五位正式选手除奖牌外还有500加元奖金
🏅加拿大前排名6-15位正式选手可以获得200加元奖金
欧几里得竞赛考试形式和内容如何?
01、欧几里得考试形式
考试语言:全英文
考试时长:150分钟
考试题型:共有10道题,总分为100分(每道题占10分)。考试包括short answer题和full solution题两种类型。short answer题只需要给出正确答案即可获得满分。
*标有黄色灯泡的为short answer,即写出答案即可。标有纸和手握笔的为full solution,即需要写出详细的答题过程。👇
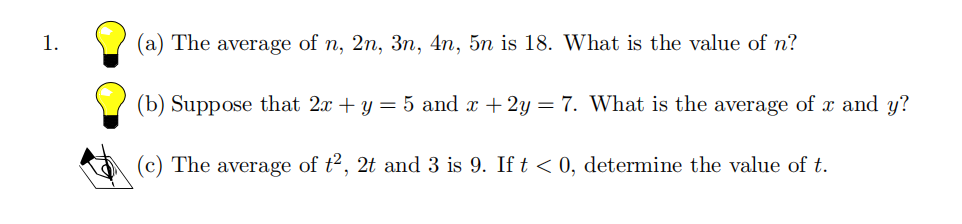
解答题的评分标准则根据详细的解题步骤来确定,即使得到正确答案也不一定能够获得满分,而相反,即使没有得到正确答案,只要解题过程正确、完整和规范,也可能获得该题大部分分数。
*考生可以使用不带编程和绘图功能的计算器,但不得使用任何可以连接互联网的电子设备,例如手机和平板电脑等。
02、欧几里得考试内容
- 方程、方程组、不等式
- 初等函数
- 多项式函数(三次方程求根、余数定理和因式定理)
- 指数函数和对数函数
- 三角函数(图像、性质、正弦定理和余弦定理)
- 数列和数列求和
- 排列组合问题
- 基础数论
- 几何(平面几何、解析几何)













