AMC8数学竞赛结束后,很多家长已经开始规划AMC10数学竞赛了。AMC10竞赛的知识点相较于AMC8来说有明显的增加,AMC8竞赛考察的知识点广却浅,AMC10竞赛不管是从知识点的难度还是解决问题的思维方式上都有进一步的提高,那么,对于AMC8数学竞赛取得20+的同学应该怎样备考AMC10呢?
大家和老师一起来看看吧,满满的干货,建议点赞收藏!
1、AMC10数学竞赛
正所谓“知己知彼方能百战百胜”,在备考AMC10数学竞赛之前,我们需要对AMC10竞赛的赛制规则、考查内容、以及奖项设置要有一个全面的了解,这样有助于同学们清晰AMC10的备考目标!
AMC10赛制要求
参赛资格:10 年级及以下学生,且在考试当天年龄不超过 17.5 周岁
考试形式:个人赛,线上考试
考试时间:每年 11 月举行,分为 A、B 两场考试
AMC10 A 卷:2025 年 11 月 7 日
AMC10 B 卷:2025 年 11 月 13 日
试卷题型:25 道单项选择题(5 选 1)
评分标准:答对一题得 6 分,未答得 1.5 分,答错得 0 分,满分 150 分。
⚠比赛中不允许使用计算器。
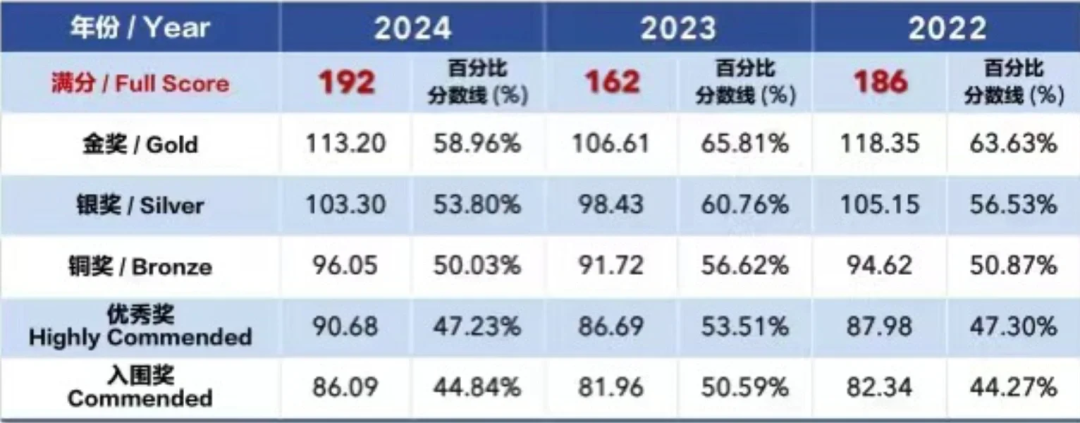
AMC10奖项设置
▪满分奖:获得满分 150 分的同学。
▪全球卓越奖:全球成绩排名前 1%,通常分数在 125 分以上,可自动晋级 AIME。
▪全球优秀奖:全球成绩排名前 5%,分数大约在 110 - 124 分之间,可获 MAA 电子证书。
▪全球荣誉奖:8 年级及以下学生在 AMC10 中获得 90 分以上。
了解AMC10数学竞赛的赛制规则之后,需要注意的是:AMC10竞赛的评分规则,答对得6分,不答得1.5分,答错得0分,因此在考试中遇到完全不会的题,宁愿不答也不要乱选。
同时,备考AMC10竞赛的考生需要清楚自己的目标,低年级第一次备考的学生可以冲刺AMC10的荣誉奖,及答对15题即可获得;高年级同学则需要把目标定高一些,往前5%和1%冲刺!
AMC10数学竞赛考试内容
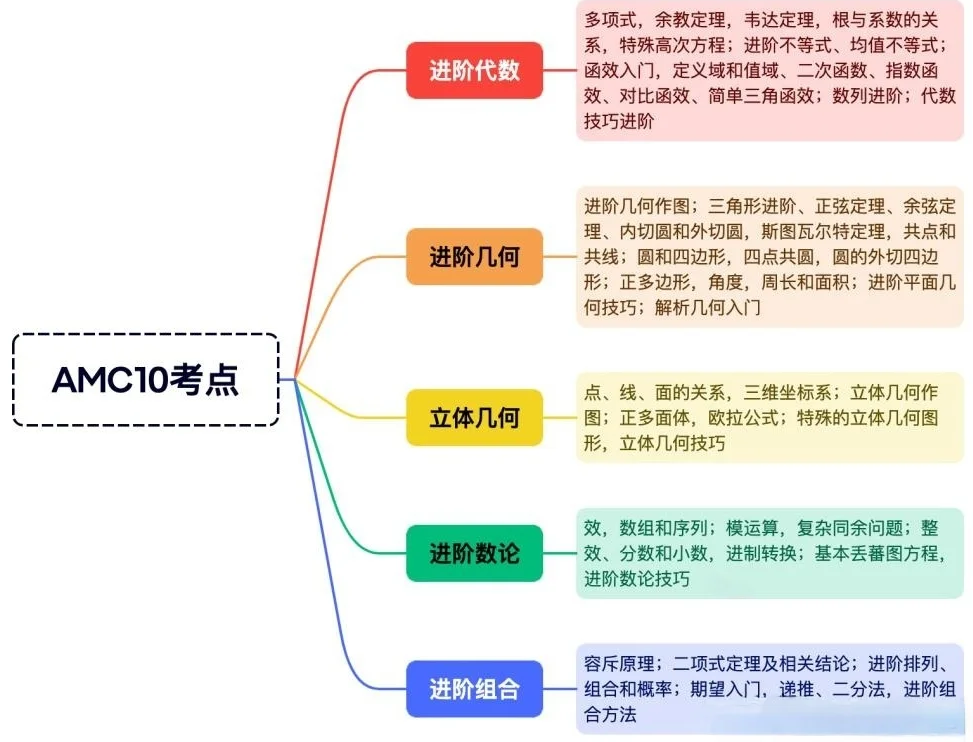
16个AMC10竞赛考点
1、数论基础:质数、 质因数分解 、因子个数定理、最大公约数、最小公倍数、欧几里得算法
2、同余和整除
3、高级定理和进制:欧拉定理、 费马小定理、威尔逊定理、中国余数定理、数位和进制、无限循环小数
4、几何基础:三角形、面积周长
5、进阶几何:相似三角形、三角形内的点线关系
6、圆:圆的基础知识、圆的高级定理
7、立体几何:线、平面和角 、坐标系下的立体几何、 多面体
8、解析几何:直线、圆
9、几何变换:平移 、位移、对称、旋转
10、加法原理和乘法原理
11、排列组合:排列、圆排列、组合和分组、 范德蒙恒等式、 容斥原理等
12、概率:古典概率 、几何概型、马尔科夫链、递推
13、数列:等差数列 、等比数列
14、多项式:代数基本定理、韦达定理的一般形式、 有理根测试、综合除法 、长除、笛卡尔符号规则 、余数定理、因子定理
15、函数及其图像:常见函数及其图像 、 高斯函数及其图像、天花板函数及其图像
16、不等式:线性不等式、高阶多项式不等式、二次不等式、柯西不等式、均值不等式
AMC10 数学竞赛相较于AMC8 竞赛增加的知识点:
✅数列:AMC10 增加了等差数列和等比数列的通项公式、递推公式及求和的深入内容,涉及非等差和非等比数列的计算。例如,需要运用数列知识解决一些实际问题,如根据给定的数列规律求特定项的值或数列的和。
✅线性函数:在 AMC10 中,要求掌握线性函数的图像、性质及解析式,能够求解线性不等式并应用于实际问题,进行直线在坐标系中的计算,以及列线性方程解应用题。这需要学生对函数和方程的关系有更深入的理解,能通过函数图像分析问题。
✅排列组合及概率:AMC10 会考察计数基本法则中的乘法法则和加法法则,深入学习排列的原理和应用、组合的应用,以及概率的计算法则及应用。比如,通过排列组合知识计算复杂事件的概率,或者根据概率问题构建排列组合模型。
✅整体运算:包括最大公约数、最小公倍数的相关计算和应用,连续整数、奇数和偶数的求和及乘积运算,各种因式分解的方法及广泛应用,指数运算的基本法则及解方程。这些知识点在 AMC10 中要求学生能熟练运用,以解决更复杂的数学问题。
AMC10竞赛的考试难点及易错点
结合AMC10竞赛的历年真题,老师给大家整理了AMC10竞赛中出现的考试难点以及易错点,帮助同学们更加顺利的备考!
代数与函数
✔高阶方程与多项式:涉及余数定理、韦达定理、根与系数的关系、高次方程的特殊解法等,常与不等式结合考查
✔函数与数列:二次函数、指数函数、对数函数的性质与图像分析,数列的通项公式与求和技巧
⚠易错点:应用题建模(单位换算、条件转化)、绝对值函数的分类讨论、复杂方程求解中的计算错误
几何
✔平面几何:三角形进阶定理(正弦定理、余弦定理、斯图尔特定理)、圆与四边形的性质(四点共圆、切圆性质)、几何变换(对称、旋转)及解析几何初步(坐标系中的直线与圆方程)
✔立体几何:三维坐标系中的点线面关系、欧拉公式在正多面体中的应用、体积与表面积计算(如球体、圆锥体)
⚠难点:几何图形的动态分析、辅助线构造技巧、复杂几何问题的多定理综合应用
数论
✔模运算与同余:复杂同余方程求解、剩余系的应用、整数解的存在性分析
✔质数与进制转换:质因数分解的灵活运用、进制转换中的数位分析
⚠易错点:同余性质误用、质数分布规律判断错误、整数解范围界定模糊
组合数学
✔排列组合与概率:容斥原理、递推关系(如斐波那契数列模型)、二项式定理的变形应用、几何概率问题
✔期望与策略问题:离散期望值的计算、动态规划思想在路径问题中的应用。
⚠难点:重复计数或漏计、复杂情境下的组合模型构建
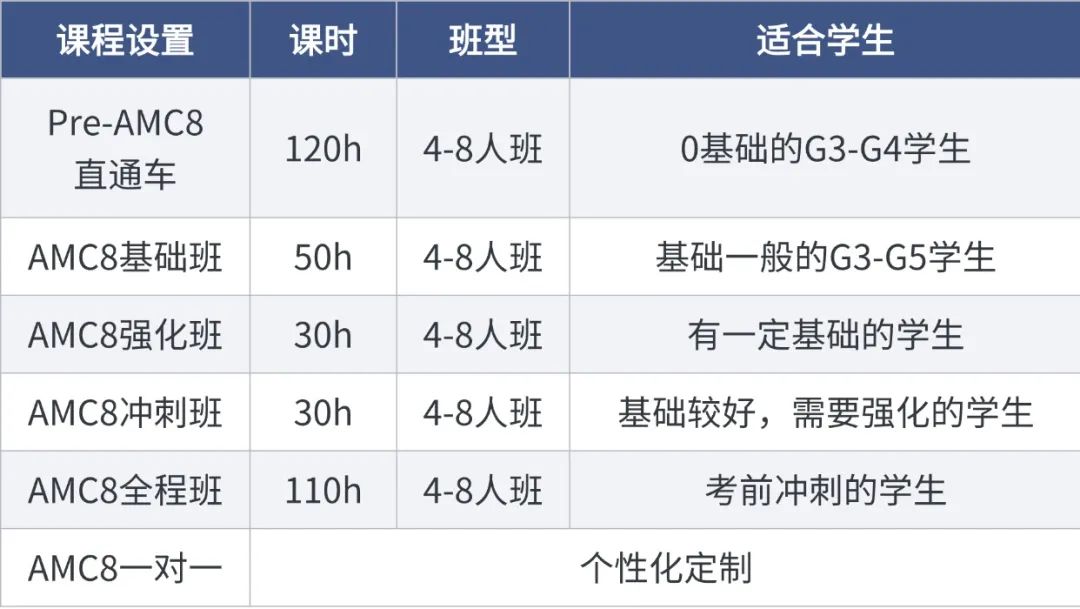
机构AMC10竞赛课程
机构针对不同基础的考生开设了Pre-AMC10直通车课程和AMC10竞赛培训课程,适合不同年龄和基础的学生。
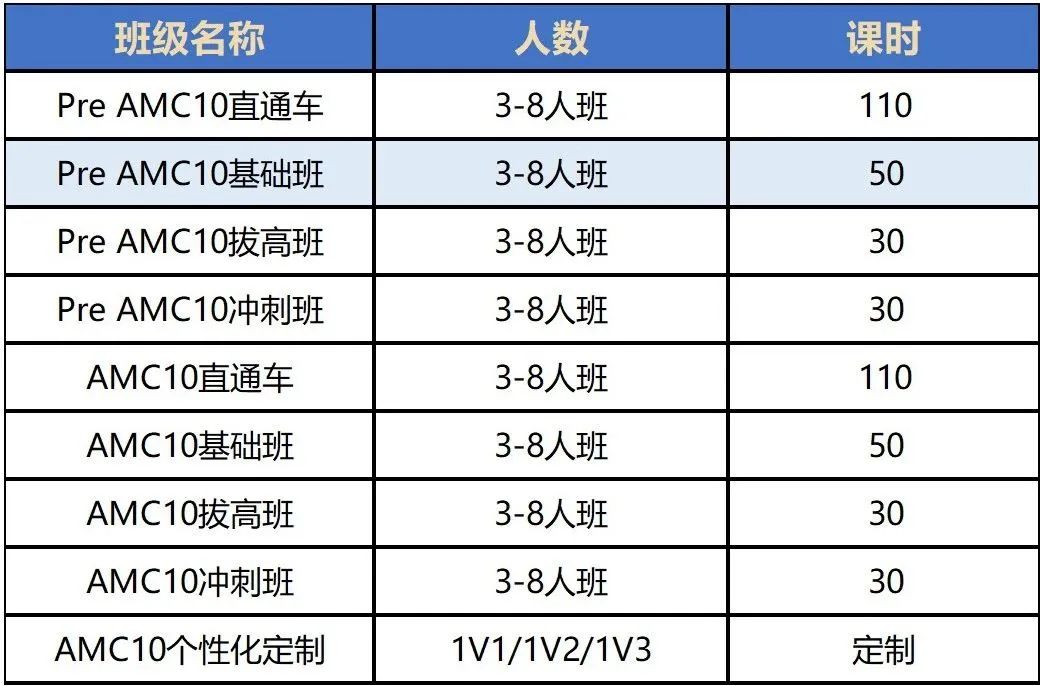
授课模式:3-8人小班教学
上课形式:线上线下同步授课,可回放
授课语言:中英双语/纯英文授课
课程亮点:入班前测,根据结果分配班级
机构AMC10竞赛培训师资
机构AMC10竞赛培训课程老师均毕业于海内外名校,拥有丰富的教学经验和AMC10竞赛辅导经验,可线上线下,中英双语教学。