作为哈佛、MIT等顶尖大学招生官高度认可的「数学能力认证书」,AMC竞赛奖项或高分可直接提升留学申请竞争力,更是晋级AIME全球数学精英赛的关键敲门砖!
AMC8数学竞赛高频考点
基础代数
代数大约有10道左右的题目,被视为AMC8考试的核心内容,是AMC8考试中历年来出现频率最高的考点之一,主要考察的知识点包括分数、方程、数列等。
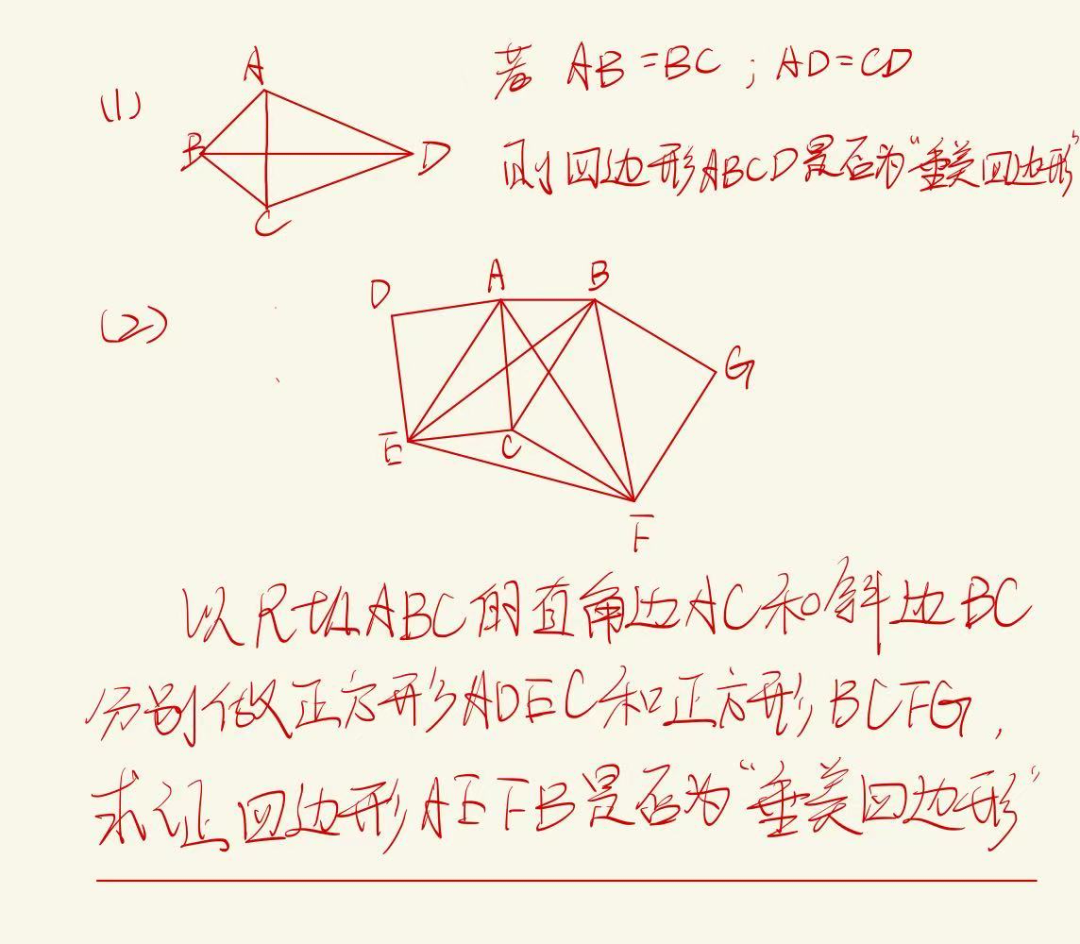
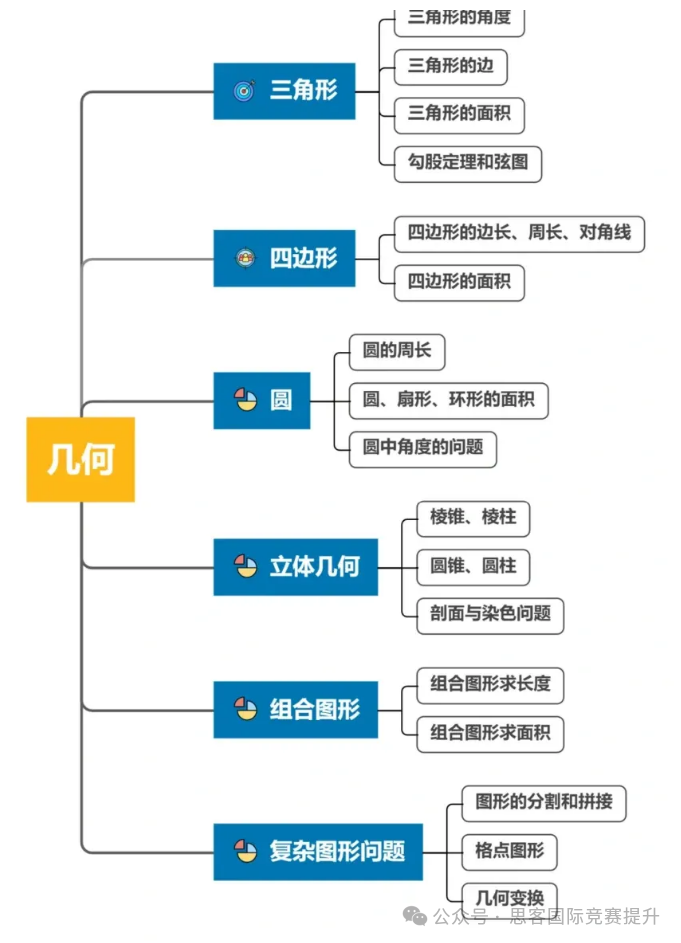
基础几何
几何的出现的次数虽然少于代数,但几何的题目数量通常会有6到8题,侧重于考察三角形、四边形和勾股定理的知识。需要注意的是,大部分几何内容在国际课程中并未涵盖,因此需要另补充相关的知识点。
基础组合
组合题目在考试中的比例较小,大约有3至5题,内容主要围绕计数和概率问题等。特别是计数题目,每年考试都会涉及到,所以需要重视和加强复习。

基础数论
虽然数论在数学考试中所占的比重没有几何和代数那么高,但近年来它的考试比重逐步提升,大约会占到3至4题。考的知识点主要包括整除性和质因数分解等。

AMC10竞赛高频考点
AMC10竞赛高频考点涵盖了代数、几何、数论和组合等多个领域,以下是具体介绍:
✅代数
多项式:包括多项式的因式分解、余数定理、韦达定理、根与系数的关系等。
二次函数与方程:涉及二次函数的图像、性质,二次方程的求解等。
不等式:包括线性不等式、二次不等式、高次多项式不等式、均值不等式等。
数列:等差数列、等比数列及其他特殊数列的性质和应用。
✅几何
相似三角形:相似三角形的判定、性质及应用。
圆的性质:圆的基本性质、圆周角定理、垂径定理、圆幂定理等。
立体几何:点、线、面的关系,三维坐标系,立体几何作图,正多面体,欧拉公式等。
解析几何:直线方程、圆的方程等。
✅数论
质数与合数:质数的判定、质因数分解等。
同余与模运算:同余方程、费马小定理、欧拉定理等。
因数与倍数:最大公约数、最小公倍数等。
✅组合
排列组合:排列数、组合数的计算,圆排列、分组问题等。
概率与统计:古典概率、几何概型、条件概率、期望值等。
容斥原理:用于解决复杂计数问题。
AMC12竞赛高频考点
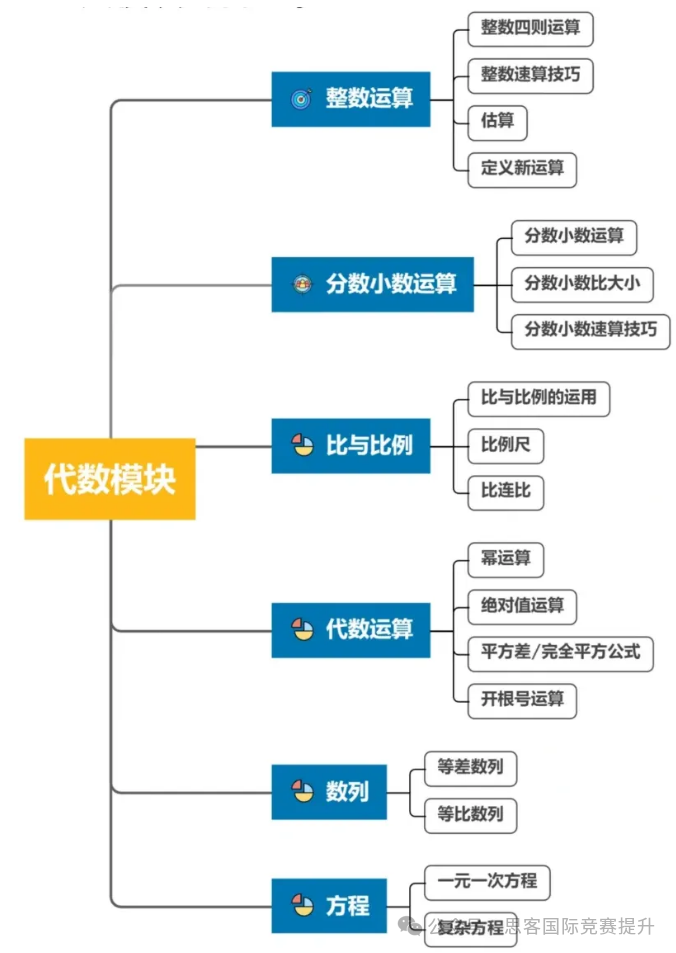
代数模块:在 AMC12 中,除常规的代数方程与函数外,对数函数、指数函数以及复数相关知识的考查较为频繁。对数函数的运算性质、对数方程的求解,复数的四则运算、模、共轭复数等都是常见考点
几何模块:平面几何中三角形、四边形、圆的性质与计算是基础,三角函数在几何问题中的应用也极为关键,如利用三角函数求解三角形的边长、角度和面积。立体几何方面,涉及棱柱、棱锥、圆柱、圆锥、球等几何体的表面积、体积计算,以及空间中直线与平面的位置关系等考点。
数论模块:整数性质、整除、同余、质数与合数等是数论模块的重点。常见题型包括求两数的最大公因数与最小公倍数、判断整除关系以及求解同余方程。
组合模块:排列组合、概率统计、容斥原理等是高频考点。排列组合中不同排列与组合方式的计算,概率问题中古典概型与几何概型的概率计算,以及容斥原理在计算集合元素个数问题中的应用,如利用容斥原理确定满足多个条件的元素个数。
⚠除此之外,还需要掌握以下板块的常用公式与定理:
进阶代数:柯西不等式、三角恒等变换(和差化积/积化和差)、复数运算(欧拉公式、复平面几何)
进阶几何:托勒密定理、圆幂定理、三维向量运算、空间解析几何
数论与组合:费马小定理、二次剩余、复杂丢番图方程;随机过程期望值计算、对称性组合问题。
AMC8数学竞赛高频考点
针对25年AMC12竞赛,机构分别开设了不同的AMC竞赛辅导班:全程班、长线基础班、基础班、提高班、高分冲刺班、串讲模考班、复习班,满足不同基础学生的参赛需求。
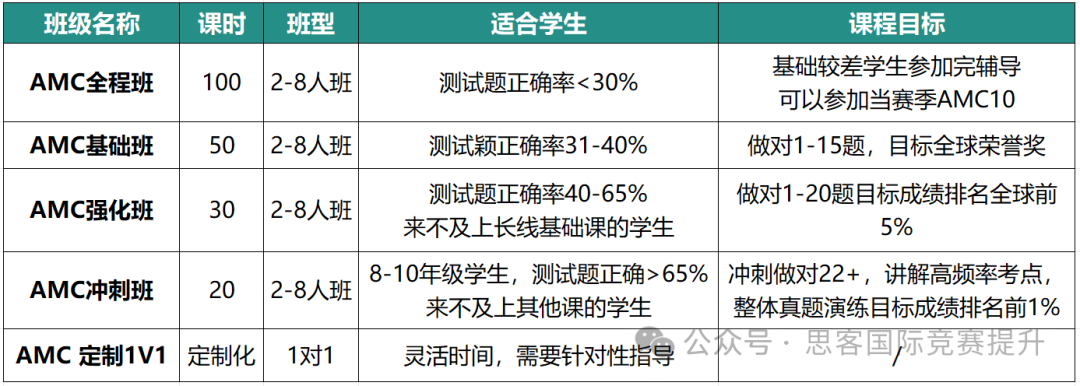
课程优势
▶课程量身打造
私人定制课前测试,根据测试结果分配合适的班课,不同班型适合不同基础学生学习。
▶师资力量优秀
主讲老师大部分为海内外名校毕业,拥有多年国际竞赛教学经验。
▶教材精编
独家优秀的教研团队研发出一套成体系化的教材和课程,能够帮助学生快速搭建一套全面的竞赛知识体系,了解自己的优势和薄弱项,进而针对性查漏补缺,冲分拿奖。
▶学习管理老师全程辅导
老师全程跟进并督促学习,课前预习提醒,课后跟进回访,实时关注学生学习动态与成长轨迹,与学生保持密切交流。