AMC10公式定理及知识点！

尽管AMC10的题型年年有所变化，但经常考查的AMC10公式定理及知识点实际上相当有限。给大家已经整理出了经常出现的AMC10公式，如果想要在短时间内迅速提升，那么认真记忆这些公式无疑是最高效的策略！

AMC10公式定理完整版

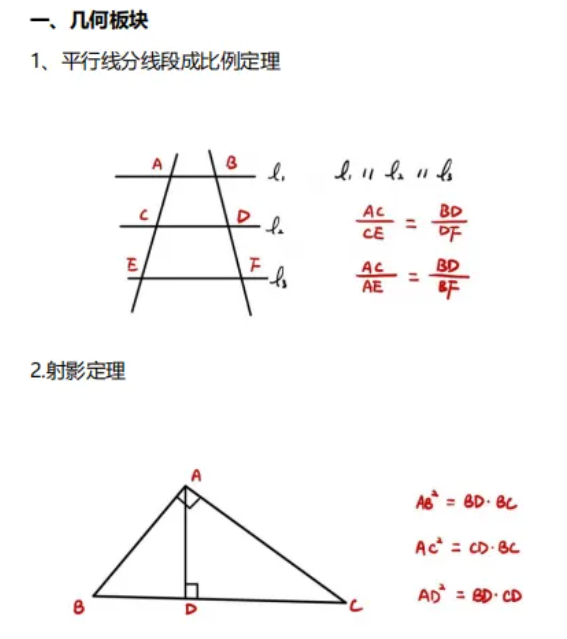
1️⃣几何板块

平行线分线段成比例定理：用于解决基于平行线的几何问题。

射影定理（Euclid's theorem）：特别适用于直角三角形的边长和角度问题。

角平分线定理（AngleBisectorTheorem）：用于解决与角平分线相关的比例问题。

正弦定理（The Law ofSines）和余弦定理（The Law of Cosines）：用于计算三角形边长和角度。

斯图尔特定理（Stewart'sTheorem）：与三角形的内切圆和外接圆相关。

2️⃣代数板块

韦达定理（Vandermonde's Theorem）：用于解决多项式根的性质。

算术平均-几何平均不等式（AM-GM Inequality）：用于比较数列的平均值。

二项式定理：用于展开二项式表达式。

合分比定理（Compound Fraction Theorem）：处理复合分数问题。余数定理：用于处理同余方程。

3️⃣数论板块

孙子定理（Sun Zi's Theorem）：用于解决多个未知数的线性方程组。

费马小定理（Fermat's Little Theorem）：与素数测试和同余式相关。

威尔逊定理（Wilson's Theorem）：与素数性质相关。

欧几里得算法（Euclidean Algorithm）：用于计算最大公约数。立方和公式：用于解决与立方数相关的问题。

4️⃣计数板块

加法原理和乘法原理：用于计数问题。

容斥原理：处理集合的计数问题。排列组合：解决顺序和组合问题。

二项式定理：再次提及，因为其在计数中的应用广泛。

AMC10常考知识点汇总

1、数论基础:质数、质因数分解 、因子个数定理、最大公约数、最小公倍数、欧几里得算法

2、同余和整除: 同余、整除、不定方程

3、高级定理和进制: 欧拉定理、 费马小定理、威尔定理、中国余数定理、数位和进制、无限循环小数

4、几何基础:三角形、面积周长

5、进阶几何: 相似三角形、三角形内的点线关系

6、圆: 圆的基础知识、圆的高级定理

7、立体几何:线、平面和角 、坐标系下的立体几何多面体

8、解析几何:直线、圆

9、几何变换:平移、位移、对称、旋转

10、加法原理和乘法原理: 乘法原理、加法原理

11、排列组合:排列、圆排列、组合和分组、 范德蒙恒等式、容斥原理等

12、概率:古典概率、几何概型、马尔科夫链、递推

13、数列:等差数列、等比数列、其他类型的数列

14、多项式:代数基本定理、韦达定理的一般形式、有理根测试、综合除法 、长除、笛卡尔符号规则 、余数定理、因子定理

15、函数及其图像: 常见函数及其图像 、高斯函数及其图像、天花板函数及其图

16、不等式:线性不等式、高阶多项式不等式、二次不等式、柯西不等式、均值不等式