2025袋鼠数学出分啦！什么水平可以衔接AMC8？

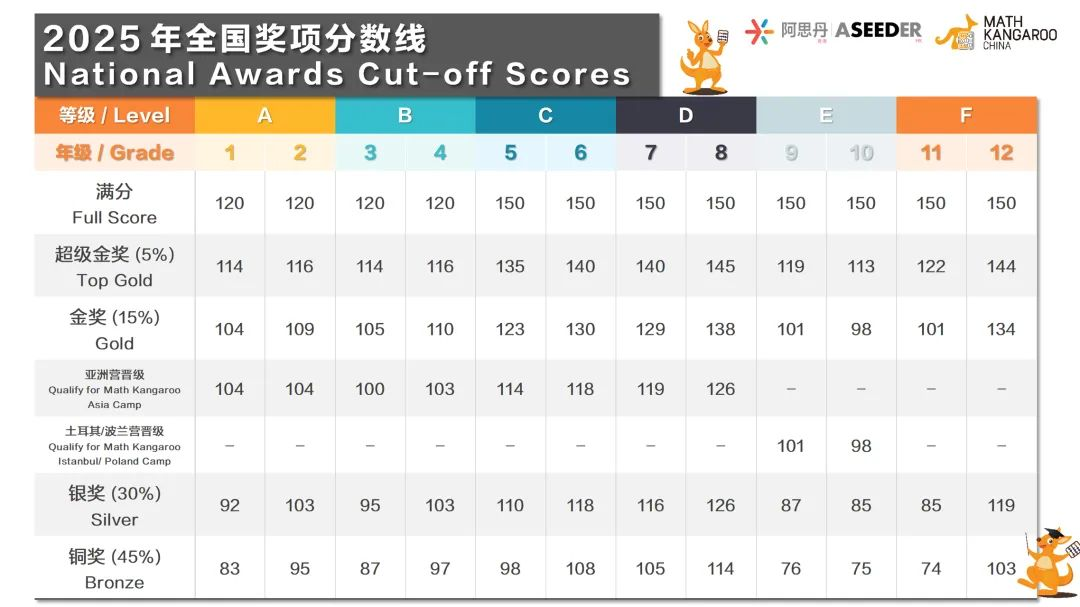
今早，2025袋鼠数学已经出分啦，今年各奖项的分数线如下图所示：

在完成袋鼠数学出分后，可能部分家长会问到，达到怎样的成绩水平可以衔接AMC8数学竞赛？

针对这个问题，回答的逻辑还是要回到这两个竞赛的知识点深度问题上。

袋鼠数学是偏向于趣味性强的竞赛类型，对低龄考试相对友好，而AMC8数学则是学术型的竞赛，选拔性更高。

对于低龄学生（如3-4年级）

通常，3-4年级学生在参加完袋鼠数学并获得【超级金奖】及以上的奖项后，仍不建议衔接AMC8，而选择参加下一级别（即L3）的袋鼠数学。因为该阶段的学生掌握的知识点仅覆盖四则运算、基础几何等，但AMC8的30%的题目已经涉及到初中的知识点，所以知识点欠缺的情况比较多。

当然，如果学生已经超前学习了全部小学阶段的知识点，也可考虑进行AMC8数学的衔接。

对于适龄的学生（如5-6年级）

该阶段的学生，已在校内学习了分数、方程、基础几何等知识点，与AMC8竞赛的知识点重复度达60%以上。如若此时学生还获得了金奖及以上的奖项，选择进入AMC8竞赛的衔接是没有问题的。

并且，对于部分超前学习的国际学校的学生，通常也在6年级左右就完成了AMC8数学的出分。

所以，如何判断学生能够衔接进入AMC8数学的学习，根本问题还是回到学生已经学习到知识点问题。

对于已完成袋鼠数学出分，且有计划参加明年1月份AMC8竞赛的学生，可选择在暑假阶段进入AMC8数学的衔接。

今年，Mentor教育也继续举行一年一度的“托福&AMC8数学奖学金计划”，只要通过考试选拔，即可拿到全额奖学金学位（即免学费），直通明年1月份的AMC8数学真考！

最后，Mentor君再补上袋鼠数学与AMC8数学的知识点衔接问题。

以上文提及的5-6年级学生为例，如若该学生已学习了袋鼠数学L3（即5-6年级）的知识点，想要衔接AMC8竞赛的，则需要重点补充以下知识点：

01数论（Number Theory）

①质数与合数

- 质数的判定方法（如试除法）、质因数分解、质数分布规律（如埃拉托斯特尼筛法）；

- 合数的性质应用，包括最小公倍数（LCM）和最大公约数（GCD）的计算。

②整除与余数

- 掌握2、3、5、9等数的整除规则，例如“能被3整除的数各位数字之和是3的倍数”；

- 带余除法的应用，同余概念及周期性问题的解法（如“今天是星期一，100天后是星期几？”）

③位值原理

- 数的十进制展开式及二进制转换基础。

02组合数学（Combinatorics）

①排列与组合

- 排列数 P(n,k) 和组合数 C(n,k) 的公式及区别（是否考虑顺序），例如“从5人中选3人排队”与“选3人组队”的差异。

②容斥原理

- 两集合公式∣A∪B∣=∣A∣+∣B∣−∣A∩B∣，三集合扩展公式的应用（如统计同时参加两种活动的学生数。

03几何（Geometry）

①圆与扇形

- 掌握圆周长 、面积，扇形弧长 和面积。

②勾股定理与立体几何

直角三角形的勾股数应用（如3-4-5三角形），三维空间中对角线长度计算。

③不规则图形面积

- 拆分法（将图形分解为规则形状）、割补法（平移或旋转补形）。

04应用题（Word Problems）

①鸡兔同笼问题

- 假设法（设全为鸡或兔，调整腿数差）与分组法（如“每只兔子和鸡分为一组”）。

②复杂行程问题

- 平均速度公式（往返路程）、相遇与追及问题的综合分析（涉及相对速度）

05计数与概率（Counting & Probability）

①加法与乘法原理

- 分类计数（如“不同颜色球的选择”）与分步计数（如“密码组合需分步确定每一位数字”）

②概率初步

- 独立事件（如连续抛硬币）与互斥事件（如掷骰子得奇数或偶数）的概率计算。

06代数（Algebra）

①线性方程组与不等式

- 代入法、消元法解方程组，一元一次不等式解集表示（如 3x>3）。

②比例与百分比

- 多变量比例分配（如混合不同浓度溶液）、利润与折扣的复合计算（如“先涨价20%再打八折”）。

07逻辑推理与数学思维

①奇偶性分析

- 利用奇偶性简化数论或组合问题（如“棋盘覆盖是否可能”） 。

②数学建模

- 将实际问题转化为方程（如“夹子与毛巾数量关系”）或图形分析。

整体而言，建议5-6年级的学生从数论（占比AMC8题量15%）和组合数学（占比AMC8题量20%）开始突破，其次再从几何中的圆和勾股定理出发。

以上，是关于袋鼠数学与AMC8数学竞赛的信息分享。