
竞赛介绍
欧几里得数学竞赛(Euclid mathematics contest)创办于1945年,是加拿大滑铁卢大学的数学学院为全球高中生举办的数学竞赛,也是加拿大最具认可度的数学竞赛,含金量极高。竞赛旨在培养学生对数学的兴趣,同时也是很好的锻炼数学解题能力的机会。对以后申请以数学和计算机著称的滑铁卢大学和该大学的奖学金都有帮助。
欧几里得数学竞赛(Euclid mathematics contest)在全世界各地的中学举行,参加竞赛的学生都有入围滑铁卢大学数学系奖学金评选的资格。竞赛成绩为列前25%的学生将获得优秀证书,且受到北美知名大学广泛认可。欧几里得是滑铁卢竞赛里知名度最高,也是加拿大最具认可度的数学竞赛,含金量极高。
竞赛含金量
①名校理工科申请加分项
成绩位于所有参赛学生的前 25% 即可获得滑铁卢大学颁发的 Certificate of Distinction 证书,不仅是滑铁卢大学或滑大数学专业认可,此证书也是申请各大学校理工专业的“敲门砖”——比如 UBC、多大工程、女王大学、滑铁卢大学,更是斩获北美名校数理工程专业 Offer 的必备证书之一,比如哈佛大学、加州伯克利分校等。
②申请滑铁卢大学奖学金的必备条件
不仅可以提高被滑铁卢大学数学系和软件工程系的录取机率,而且还可以获得相应的入学奖学金(加元1000—8000不等)。在参赛学校成绩最高的学生会获得一枚奖牌,加拿大及全球成绩优异的参赛者会出现在相应的光荣榜上,并获得相应奖金。参加并获得欧几里得赛事的奖项是申请滑铁卢大学奖学金的必要条件,同时欧几里得比赛也是众多藤校颁发奖学金的重要指南。
竞赛信息
1、适合学生
任意年级高中生(9-10年级数学基础比较好的同学也可以尝试)
2、竞赛时间
报名截止时间:2023年3月10日
竞赛时间:2023年4月5日
3、竞赛形式
2.5小时,共10道题,总分为100分
简答题、全解题
(注意:需要学生完整表达解题过程。根据解题的方法和步骤获得相应的分数,步骤不完整的解题无法得到全部的分数。)
大部分问题为高中难度数学题,基于高三或者12年级数学课学习的内容,最后几题为高等数学难度题目,适合数学较好的学生挑战。
欧几里得数学竞赛是线下笔试题,每题难度依次上升,考试过程中可以使用计算器,但是对型号有要求,具有通信功能,存储功能,画图功能的计算器是不可以使用的
奖项设置
个人奖项
Certificate of Distinction:
在全球参赛者中排名前 25%的学生均可获得证书
Contest Medal:
由CEMC颁发给每个学校的冠军
Honour Rolls:
分加拿大地区正式,加拿大地区非正式以及国际区域的高分参赛选手会被分别在各区域荣誉榜提名
Plaque:
加拿大前五位正式选手除奖牌外还有500加元奖金
加拿大前排名6-15位正式选手可以获得200加元奖金
团队奖
学校可选择性参加团队成绩的评比,成绩为3位最高分正式选手的成绩总和
加拿大区域可评3中等级的奖项:Zone,Provincial,National
加拿大的学校可以评 Canadian Championship Plaque, Provincial Championship Plaques, 和 Zone Championship Certificates
竞赛内容
✔️多项式的分析以及方程组的求解
✔️指数和对数的分析
✔️几何与解析几何(正方形,圆形)
✔️等差数列与等比数列
✔️函数的基本性质
✔️三角形与三角函数
✔️排列组合问题
✔️排列组合细节分析
✔️质数与因数的分析
从难度而言,欧几里得数学竞赛大部分问题为高中难度数学题,基于高三或者12年级数学课学习的内容,只比高中数学的教学大纲稍稍高出一点。
欧几里得数学竞赛有考察比较稳定的特性,常考的知识点如下:
✔️排列组合与概率是必考考点,一般都会放在第5-7题或者在第10题结合其他模块考察。
✔️三角恒等与三角函数或求解三角函数的题目一般会放在7-9题,与对数题并称中国考生福利题。中国考生对这两个都比较熟悉,处理这些偏计算的题型时优势比较明显。
✔️数论题目在欧几里得数学竞赛出现的不多,常常是与计数结合,会放在第9或第10题。
题型涵盖解答题和全解题,共10道题目,每道题2-3问。对于大部分中国学生来说拿到前25%的难度不大,但想拿到前5%或者顶级成绩,还是有一定难度的。
因为前8题的难度适中、题型比较稳定,且门槛不高的特点;最后2题为高等数学难度题目,对标准的中学数学竞赛来说略显超纲,适合数学较好的学生挑战!
6道必考题
1)Logarithms and Exponents是一道10分的题,关于指对数的化解;
2)Functions and Equations方程如何修解;
3)Analytic Geometry研究角度、相似三角形等;
4)Trigonometry考试时会用到sin, cos, tan的公式,是同学们的弱项;
5)Sequences and Series是11、12年级课本上没有的;
6)Circle Geometry是有关于圆的内容
竞赛难点
难点一:题目前后差距
根据往年的经验来看,保证前7道题全部做对就可拿奖,做对问题不大,拉开差距拿顶级分数的关键就在8-10题。前面几题属于常规中学数学题难题,但是最后几题是用来挑战全球顶尖学生思维的。
难点二:清晰解题步骤
欧几里得需要学生完整表达解题过程,根据解题的方法和步骤获得相应的分数,步骤不完整的解题无法得到全部的分数。
难点三:知识点的综合应用
欧几里得难题部分会经常出现知识点的综合应用,像几何叠加复杂方程组、几何叠加不定方程、数列叠加复杂方程组、数列叠加不定方程,需要同学们掌握知识点后,反复练习。
竞赛有专门的一套知识体系,而且竞赛最主要是对数学公式定理这些工具的灵活运用和快速选择上,因此竞赛准备更需要成体系的训练。
近年分数线
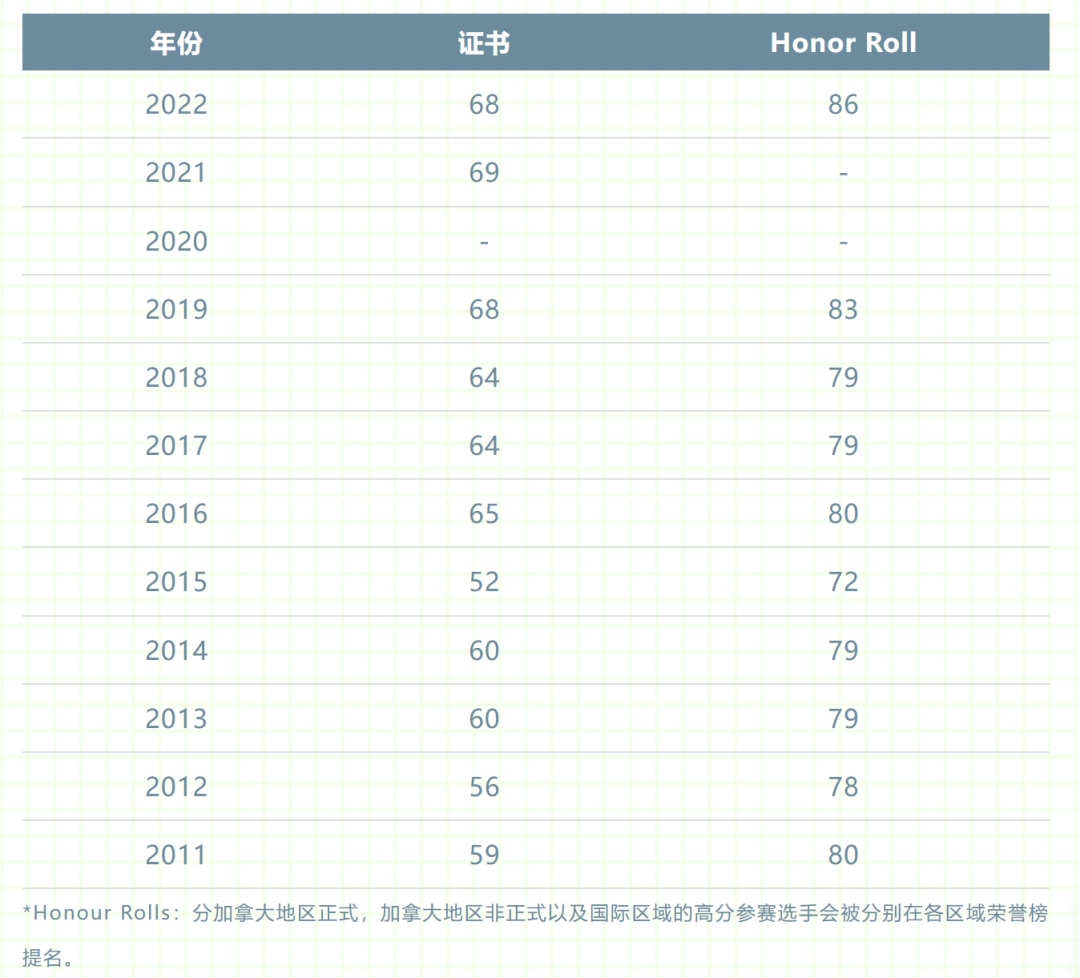
从近十年的数据来看,欧几里得的获奖分数整体呈上升趋势,从2016年起获得Certificate of Distinction荣誉的分数稳定在60分以上,而Honor Roll荣誉的分数线较稳定,一直维持在80分左右,2022年高达86分。因此,获得欧几里得证书要做对七道题左右,2022年获得欧几里得证书是68分,拿下Honor Roll荣誉需要86分,也就是做对八道题以上。
竞赛真题














