数学是高中阶段重要的基础学科,不论是未来想往理工科方向发展的学生,还是往文商科方向发展的学生,都需要具备扎实的数学功底。Himcm数学建模是一个非常不错的选择,那它的获奖比例高吗?一起来看看特等奖论文是怎么样的?

1、Himcm赛制要求
📌参赛对象:适合14岁半或以下在校初中生,需要2-4人组队参加。
📌竞赛形式:在为期14天内,参赛队伍根据实际问题来建立数学关系进行求解。HiMCM数学建模竞赛为命题论文(A/B题二选一),需要为他们选择的问题提交一个解决方案,并最终完成赛事论文的提交。
🔹HiMCM团队最多由4名同一所学校注册的高中生组成;
🔹每队必须配备一名指导导师;
🔹提交的论文必须为英文PDF格式;
🔹每道问题都没有封闭性的答案。
📌竞赛要求:竞赛时可以用书本、计算、软件、网络等资源,但不能和队外的任何人(包括本队的指导老师)进行任何方式的讨论。竞赛结束后向COMAP递交答卷,由COMAP组织专家评阅。
📌竞赛时间:美东时间11月2日-11月15日
📌奖项设置:
🏆特等奖(National Outstanding):前1%
🏆决赛入围奖(Finalist):数量不超过队伍总数的7%
🏆一等奖(Meritorious):数量约占队伍总数的12%
🏆二等奖(Honorable Mentioned):数量约占队伍总数的31%
🏆参与奖(Successful Participate):成功完成建模论文的队伍
HiMCM数学建模竞赛需要参赛选手具备一定的编程技巧,但还是更强调数学,逻辑思维和论文写作能力。这项赛事是借鉴了美国大学生数学建模竞赛的模式,结合中学生的特点进行设计的。
2、获奖比例
第二十六届(23年)美国中学生数学建模竞赛(HiMCM/MidMCM)来自 18 个国家/地区四百多个学校的 1042 个队(其中 HiMCM 967 队,MidMCM 75 队)参加了本次比赛。
比赛共设置五个等级的奖项:特等奖(Outstanding)、提名奖(Finalist)、一等奖(Meritorious)、二等奖(Honorable Mention)、参与奖(Successful Participant)。对于未能提交论文或提交的论文不合格的参赛队,则被标记为不成功(Unsuccessful)。各奖项统计结果如下:
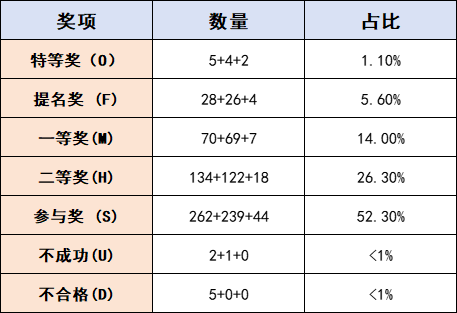
本次比赛共评出11篇特等奖论文,其中A题5篇、B题4 篇、C题2篇,具体如下:
A 题:
Dandelions: Friend?
Foe? Both? Neither?
🔺13643 Shanghai World Foreign Language Academy, Shanghai, China
🔺13719 Nanjing Foreign Language School, Jiangsu, China
🔺14076 Shanghai Pinghe School, Shanghai, China
🔺14140 Shanghai Pinghe School, Shanghai, China
🔺14632 Mass Academy of Math & Science, MA, USA (NCTM Award)
B 题:
Charging Ahead with E-buses
🔺13694 St. George's School, BC, Canada
🔺13904 Shanghai Starriver Bilingual School, Minghang, China
🔺14087 BASIS International School Guangzhou, Guangdong, China
🔺14323 Durham Academy, NC, USA (NCTM Award)
C 题:
Preparing for Olympic
Medal Ceremonies
🔺14255 BASIS Independent Silicon Valley, San Jose, CA, USA
🔺14749 Shanghai American School, Shanghai, China (NCTM Winner)
3、Himcm论文标准
一篇出色的HiMCM数模论文需要基本满足以下要求:
一、论文结构与内容
引言(Introduction)
重述并澄清赛题,明确解题目标,澄清原题叙述上可能出现的模糊概念。
综述与评论现有研究结果,为建模过程提供背景。
简要介绍解题思路和主要方法。
摘要(Abstract)
摘要必须按要求写在特定的摘要页上,长度不超过一页。
简要概述论文的主要内容和结论,主要回答以下问题:针对问题、建立模型、求解方法、主要结果、评价及主要推广。
表述通顺、规范、准确,重点突出模型、算法、结论、创新点等。
假设条件(Assumptions)
列出建模所用的所有前提条件及假设,并给出清晰的解释(包括符号说明)。
对于重要的假设条件,用列表或编号的方式逐条陈列出来。
建模动机与合理性(Justification of Approach)
分析赛题,给出建模的动机或论证建模的合理性。
详细描述所设计的模型,包括其工作原理和如何解答赛题。
对于复杂模型,可以分小节描述不同的部分。
模型建立与求解
数学模型要求完整、简明、正确,明确说明简化思想、基于分析简化后的模型。
命题叙述规范,论证严密,说明计算方法或算法的原理、思想、依据、步骤。
题目中要求回答的问题、数值结果、结论,需一一列出。
结果表示要集中、直观、凸显,便于比较分析。
数据分析与验证
明确数据的来源,确保数据的可靠性和准确性。
运用统计和数学方法分析数据,验证假设,优化模型。
使用不同的数据集或场景测试模型的准确性和稳定性。
结论与讨论
概括研究内容,包括提及所引用的内容。
讨论模型的优缺点,并给出明确的结论。
提及模型的局限性和未来改进方向。
参考文献
列出论文中引用的所有文献和资料,确保格式规范。
4、机构Himcm竞赛辅导
培训体系
HiMCM数学建模培训营专门为辅导美国高中生数学建模挑战而设。
👉通过数学建模知识的培训,让学生掌握数学建模能力,从而能够面对真实情况,冲刺美国高中生数学建模活动。
👉专业导师授课,保证学生能够掌握研究问题、解决方案的能力,同时培养团队协作精神,这些能力和精神将是美国名校所看重的。

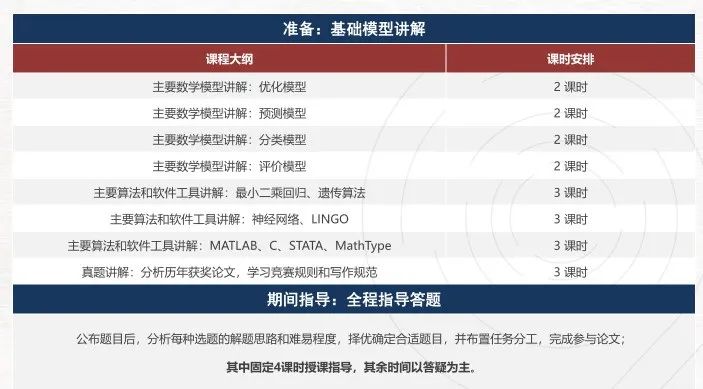
课程安排