很多同学喜欢在做题时采用数形结合的方法，因为有时候数形结合的方法的确稳准狠，而且非常直观，容易理解。在面对不等式问题时，很多同学也经常采用数形结合的方法来解题。
首先我们来看一道常规的题目，来感受一下不等式问题中数形结合的作用：
这道题目要求我们找出在给定的不等式系统中，哪个点 (x,y)是解。
◾给定的不等式系统是： y≤x+7
y≥−2x−1
假如不使用数形结合的方法，我们会需要分析每个选项，看哪个点满足这两个不等式。
选项 A：(−14,0)
将−14 代入 x ，0代入 y ，在不等式 y≤x+7 中，得到0≤−14+7，即0≤−7，这是错误的。
选项 B：(0,−14)
将 0 代入 x和−14 代入 y，在不等式 y≥−2x−1中，得到−14≥−2(0)−1，即−14≥−1，这是错误的。
选项 C：(0,14)
将 0 代入 x 和 14 代入 y在不等式 y≤x+7中，得到 14≤0+7，即 14≤7，这是错误的。
因此，只有选项 D (14,0)满足这两个不等式，所以正确答案是 D。
但是通过数形结合，不难发现D一定是正确的答案，所以马上得到正确答案。
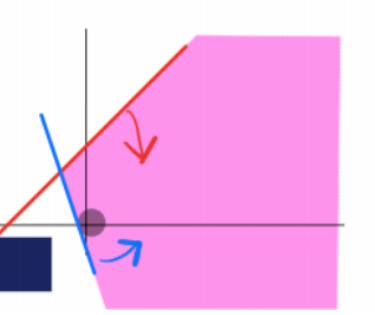
借助数形结合，第一道繁琐的题目被我们化简为一道送分题。
总之，数形结合是我们在解决不等式问题时常用的方法，但是，这个方法不是万能的，直觉解题有时候的确稳准狠，但是也会带来较大的风险。我们来看以下这道题：
Large cups and small cups cost 1 dollar each, with the large cup holding 1 liter of water and the small cup holding 0.2 liters of water. There is only 3.5 dollars available to buy cups, and the total capacity of the purchased cups must be at least 1.5 liters. How many small cups can be bought at most?
价格限制：1x+1y≤3.5（因为只有3.5美元，每个杯子1美元）
容量限制：0.2x+y≥1.5（至少需要装1.5升水)
★如图，阴影部分覆盖了所有可能的整数解
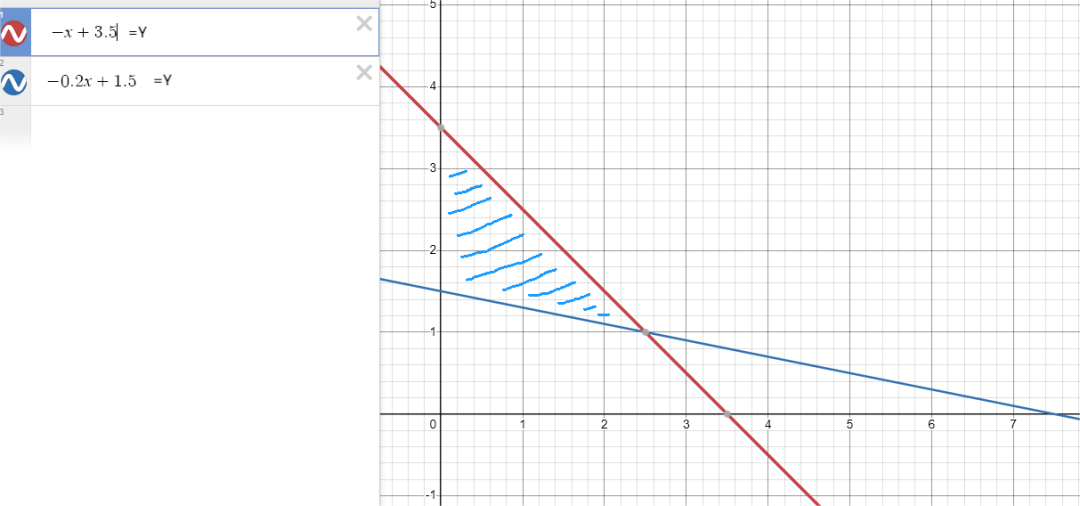
两个线性方程交于(2.5,1)，初看起来，这个最优解可以简单地舍入取得整数解，满足整数约束，即x=2.
又是一道送分题？不！这是一道“送命题”！
通过进一步的仔细观察，你会发现，x=2不是可行解，更谈不上最优解，这种方法不可取。如下图：
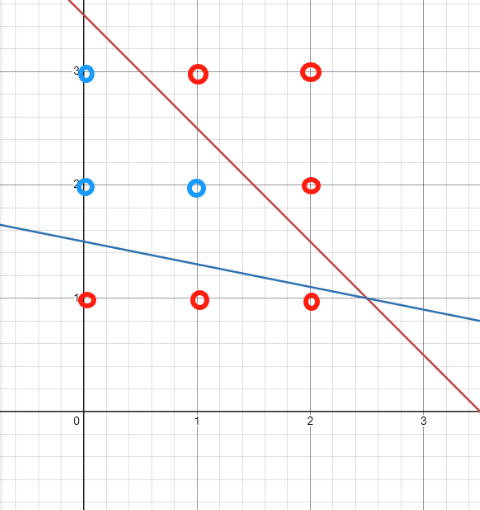
那么，由约束条件和图像，该问题的整数解只有3 个，根据图像，最多购买一个small cup。
我们来总结一下，数形结合是我们在解决数学问题时常用的方法。借助数形结合，第一道繁琐的题目被我们化简为一道送分题。
但是，这个方法被用于求解整数不等式问题时会遇到麻烦，容易让我们陷入陷阱之中，而且画图也不方便，因为挨个寻找并且标记整数解也不是一个轻松的活儿。
那么，求解整数不等式问题时，有没有更可靠的方法呢？当然，下节课我们将介绍解决整数不等式问题的通法，而为了彻底理解这个方法，我们需要回顾不等式的基本性质。
【竞赛报名/项目咨询请加微信：mollywei007】
