SAT数学 | Digital SAT中的整数规划技巧

在<送分题？送命题！-----不等式问题中数形结合的作用与局限性>这一专题,我们详细说明了数形结合的局限性,也就是完全依赖图像解题的风险。以下是上个专题遇到的题目：

Large cups and small cups cost 1 dollar each, with the large cup holding 1 liter of water and the small cup holding 0.2 liters of water. There is only 3.5 dollars available to buy cups, and the total capacity of the purchased cups must be at least 1.5 liters. How many small cups can be bought at most?

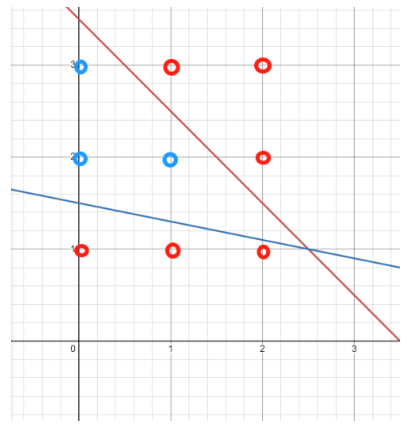
可见，很难由图直接判断不等式系统的最大整数x值是1还是2。

实际上，寻找一个双变量不等式系统的最大或者最小整数解是在DSAT考试中经常见到的问题,再比如这一道题:

A cargo helicopter delivers only 100-pound packages and120-pound packages. For each delivery trip, the helicopter must carry at least 10 packages, and the total weight of the packages can be at most 1,100 pounds. What is themaximum number of 120-pound packages that the helicopter can carry per trip?

那么遇到这种类型的习题，我们该怎么办呢？介绍解决此类问题的方法之前，我们需要掌握不等式系统的一个基本性质:

在数学中，传递性(transitive)常用于证明不等式链。例如，如果我们知道 a<b和 b<c，那么我们可以推断出 a<c。

这个性质来源于一个更基础的定理，如下:

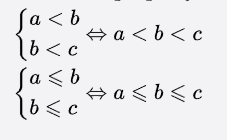
这里⇔符号表示等价关系，比如 a<b<c, 等价于 a<b 且 b<c。

好，请记住a<b<c等价于 a<b 且 b<c(当然，≤，≥，>的情况类似)。之后，让我们继续看这道题：

与前面的题目类似，我们有一个双变量不等式系统，其中 x和 y都是非负整数，我们需要求出不等式系统的最大或者最小变量。这道题的不等式系统如下：

1.x+2y≤1

2.2x+y≥1

◾目标是找到 x 的最大值。

面对这种类似的情况，我们有一个统一的处理方法，首先第一步是变量分离:

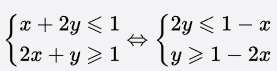
第二步,构造出a≤b且b≤c中的b

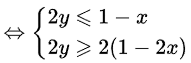
第三步,构造出a≤b≤c

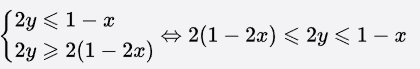
最后使用transitive property,a≤b≤c可以推出a≤c

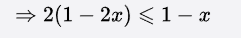
由于题目并没有考察y的取值范围,我们当然可以忽略2y，直接由a≤b≤c推出a≤c。

我们把不等式系统化简为单个不等式了，接下来就简单了，我们有1/3≤x。

又因为x是非负整数，所以x的最小值是1。如图:

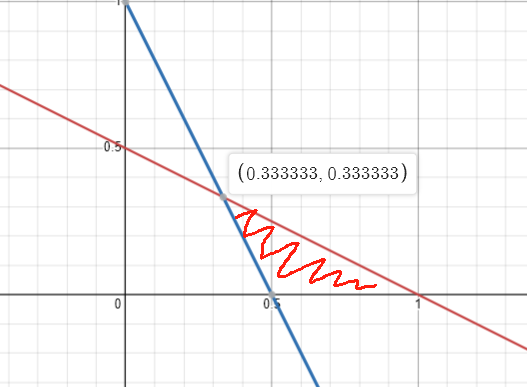
那x的最大值呢？由图可得到，也是1。

换句话说，图中的阴影部分只覆盖了一个x点，那就是x=1。

★总结这种题型的处理方法:

1.变量分离，构造中间变量

2.构造不等式链

3.求整数解

4.画图佐证

★口诀是”肿脸真土”：

肿(中)：通过分离变量构建中间变量，也就是不等式链的b。

脸(链)：通过b来串联条件，构建不等式链。

真(整)：求解整数解，确保答案准确。

土(图)：绘图辅助证明，直观展示结果。当然,有时候某些最值由图可得。如以上题目的最大值。

本次专题分享我们只介绍了不等式以及不等式系统的一个性质:transitive property。那么不等式以及不等式系统中还有没有其他需要留意的知识点或者易错点呢?答案是有的，我们在下一节专题分享中会介绍。