SAT数学 | Digital SAT不等式问题中的四大坑

相信同学们在处理DSAT 中的不等式问题时，经常会不知不觉地掉进题目的陷阱里。譬如：在处理不等式问题时，常见的四大易错点包括：

1. 忘记变量的整数特征：忘记某些变量的限制条件为整数，可能会影响解的完整性，或者遗漏一些条件。

2. 选择错误的整数规划方法：画图直观但可能不适用于复杂问题；使用不等式链适合逐步解决问题。应根据问题选择方法。

3. 遗漏不等关系：在处理多个不等式时，容易忽略某些关系，导致解集不完整。

4. 用错不等号：错误地使用“大于或等于”（≥）和“大于”（>）会导致解的性质改变。写不等式时，应仔细检查不等号的方向。

要避免这些错误，练习和反思是关键。那么废话不多说了，下面我将逐一解释这些易错点，并给同学们出一些建议：

1. 忘记变量的整数特征：

- 在解决不等式问题时，如果一个或多个变量被限制为整数，这可能会限制解的范围。

- 建议：在开始解题之前，明确变量是否为整数，以及哪些变量是整数，并在解题过程中始终记住这一点。

★例子：

Data set A consists of 10 positive integers less than 60. The list shown gives 9 of the integers from data set A.

43,45,44,43, 38, 39,40,46,40

The mean of these 9 integers is 42. If the mean of data set A is an integer that is greater than 42,what is the value of the largest integer from data set A?

题目信息

- 数据集A包含10个小于60的正整数。

- 已知9个整数：43, 45, 44, 43, 38, 39, 40, 46, 40。

- 这9个数的平均值为42。

- 需要找出第10个数，使得整个数据集A的平均值也 是一个大于42的整数。

解题步骤

1.1 计算已知9个数的总和：

总和 = 43 + 45 + 44 + 43 + 38 + 39 + 40 + 46 + 40 = 378

1.2 设定未知数：

设第10个数为 x

1.3 建立方程：

数据集A的平均值大于42，可以表示为：

（378 + x）/ 10 > 42

（378 + x）> 420

也就是 x > 42

1.4整数特性：

- 已知 x 必须小于60。

- 由于 x 必须使得 平均数是整数， 378 + x 必须是10的倍数。

1.5 确定 x 的值：

378 + x 需要是10的倍数，所以x 的个位数必须是2，在42到60之间，个位数为2的整数只有52。

这个问题体现了在处理涉及整数的问题时，不仅要考虑到哪些变量是整数，还有考虑到底多少个变量是整数，在这道题，数字本身是整数，还要确保平均值也是整数，这样子就涉及到数字的整除性和个位数的特性。

2. 整数规划方法选择：画图还是使用不等式链：

双变量不等式系统约束下的整数规划问题求解在 DSAT 专题的 第二期 《 Digital SAT中的整数规划------“肿脸真土”》有详细说明，感兴趣的同学可以回顾一下，此处只做总结。

整数规划求最大值最小值的方法往往不一样，有时使用不等式链，有时直接看图，如下所示：

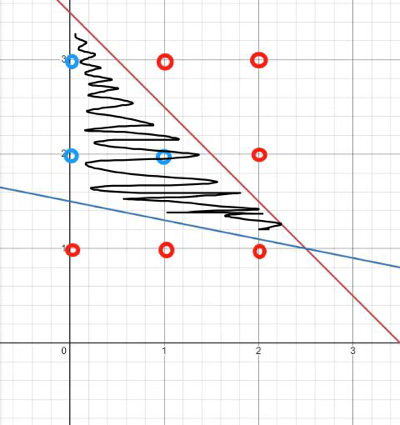
由图可知，阴影部分的最小非负整数横坐标显然是 0，阴影部分的最大非负整数横坐标是 1 还是 2，借助图像并不容易看出来，不得不使用不等式链。

3. 不等关系遗漏：

- 在处理多个不等式时，可能会遗漏某些不等关系，导致解不完整或错误。

- 建议：仔细思考变量是不是两边有界，确保没有遗漏任何关系。

★ 例子：

答案是D，需要注意的是，变量 p 有上界，因为是从 150 人中选择 p 个人，所以 p 一定小于或者等于 150。

4. 不等号用错：

- 不等号的方向错误可能会导致错误的解。例如，将“大于等于”误写为“小于等于”。

- 建议：记得不等式方向发生变化有以下两种情况：

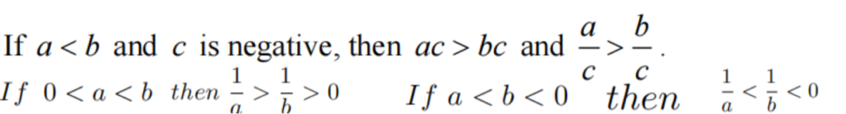
- 区分“大于或等于”（≥）和“大于”（>）是解决不等式问题的关键。前者包括边界值，而后者不包括。

- 建议：在写不等式时，区分题干中的 at most 和 less than。

以上是不等式问题的四大易错点，所以，在解决不等式问题时，始终保持清晰的逻辑和仔细的检查是非常重要的。此外，对于复杂问题，可能需要使用数学技巧和画图方法来辅助解决。