一、数学780+:
高频考点、Desmos实战与错题管理
数学是SAT冲刺高分的核心模块,需从知识点、工具应用到错题复盘全面突破。以下结合全新例题与深度解析,助你稳拿780+。
1. 高频考点深度解析与例题实战
1、代数与函数
🔸 核心公式与题型:
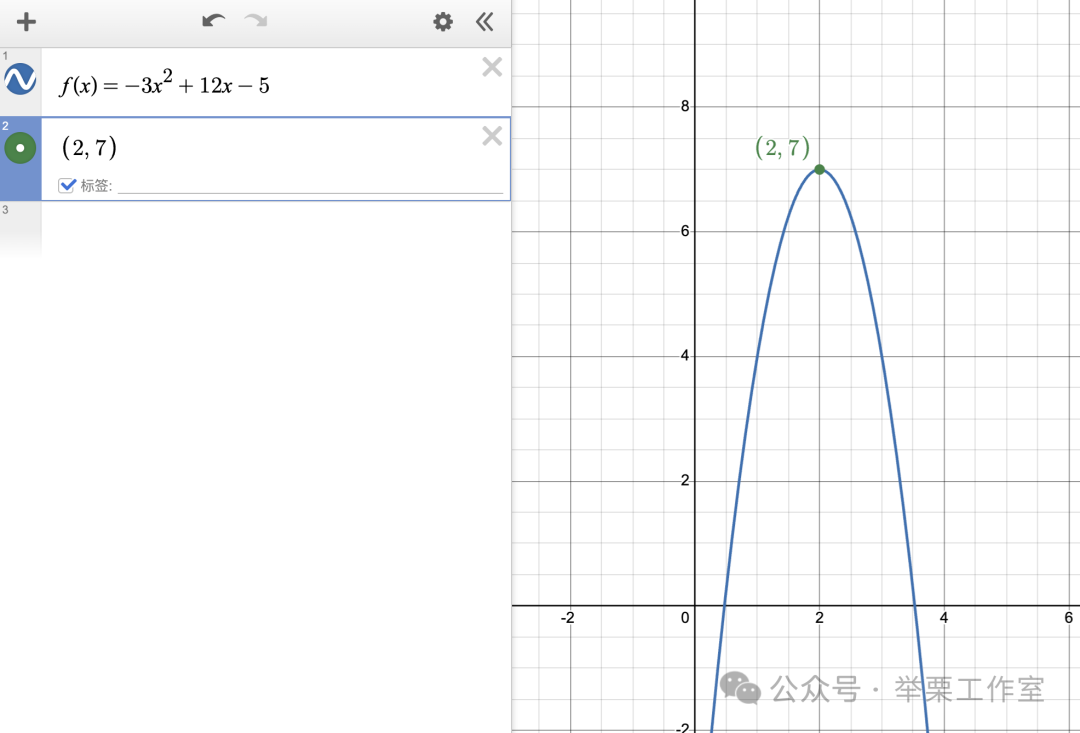
❖ 二次函数顶点公式:
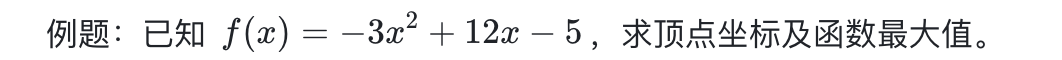
解题思路:
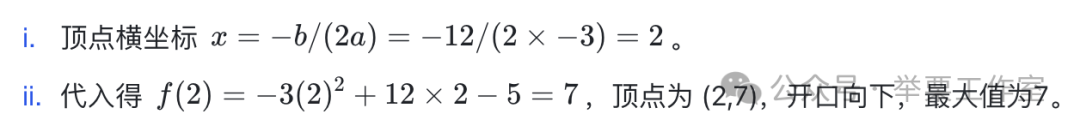
Desmos操作:输入函数表达式,点击顶点直接显示坐标。
❖ 指数模型应用:
例题:某细菌数量每2小时翻倍,初始数量为100,求24小时后的数量。
解题思路:
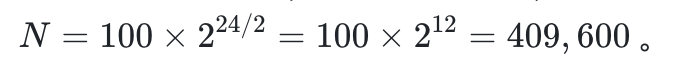
2、几何与三角
🔸 圆与三角函数高频题:
❖ 圆方程与切线:
例题:圆心为(1, -2),半径为4,求过点(5, -2)的切线方程。
解题思路:
点(5, -2)在圆外,切线斜率为0(水平线),方程为 y=−2。
Desmos操作:绘制圆与切线,确认无交点。
❖ 三角函数恒等式:
例题:若sinθ=3/5,且θ在第二象限,求 cosθ。
解题思路:
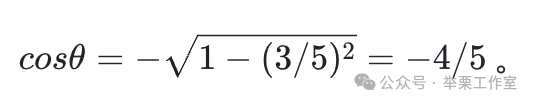
3、数据分析
🔸 Standard Deviation与数据离散的关系:
- SD越大,数据离散
- SD越小,数据集中
2. Desmos高阶应用:全新例题与分步操作
A
绘制函数图像:定位关键点
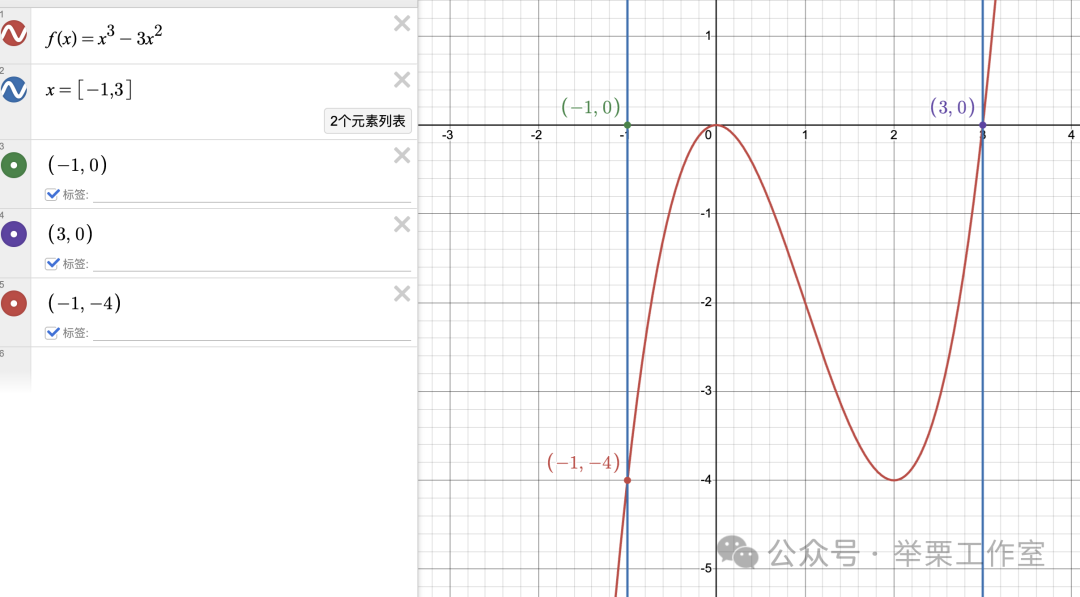
🔸 例题:函数 f(x)=x^3−3x^2 在区间 [-1, 3] 上的最大值和最小值。
解题思路:

Desmos操作:
输入函数并设置x范围[-1,3],点击图像查看极值点,对比计算结果。
B
解方程:联立方程组的图形化解法
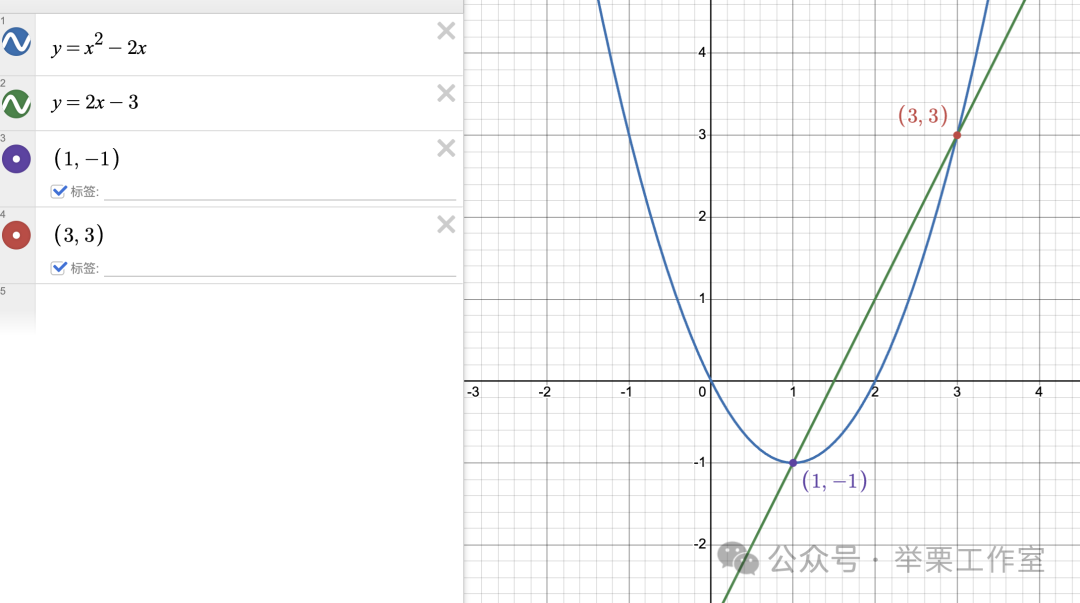
🔸 例题:求解非线性方程组:
解题思路:

Desmos操作:输入两个方程,查看交点坐标,直接验证解的正确性。
C
解不等式:图形化分析解集
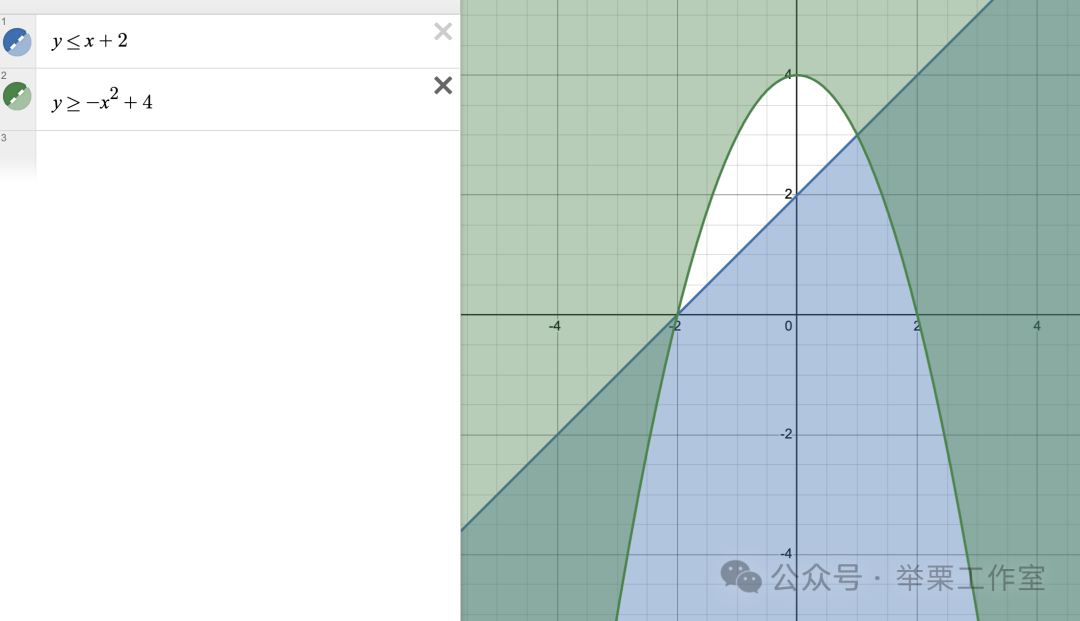
🔸 例题:求解不等式组:
解题思路:

Desmos操作:输入不等式 y≤x+2和 y≥−x^2+4,观察阴影重叠区域。
D
表格功能:动态验证函数关系
🔸 例题:已知函数 f(x)=2^x,求当x=0,1,2,3时的函数值,并判断增长趋势。
Desmos操作:输入函数,创建表格并输入x值,表格自动计算y值(1,2,4,8),验证指数增长特性。
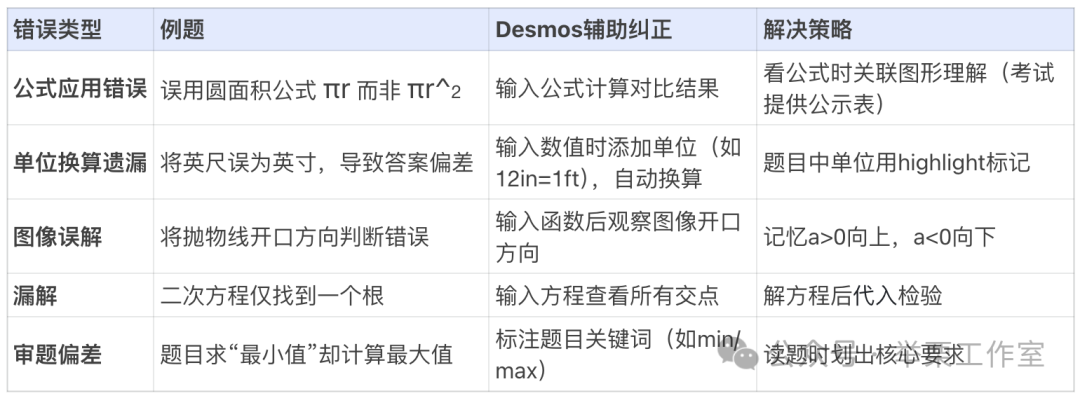
3. 错题分类模板升级:5大常见错误与解决方案
二、英语720+:词汇、阅读与文法的系统突破
1. 学术词汇:词根词缀与场景记忆法
🔸高频词扩展:

🔸长难句拆分实战:
例句:"Despite the initial skepticism from critics, the theory, which integrates quantum mechanics and relativity, has been widely accepted by physicists."
拆分步骤:
1. 主句:The theory has been accepted。
2. 修饰成分:Despite...(让步状语),which...(非限定性定语从句)。
2. 阅读提速:三步定位法与文体策略
🔸科学类文段:
1. 重点抓“假设-实验-结论”结构,细节题答案多出现在数据描述部分。
2. 例题:“The experiment aimed to test whether caffeine affects memory retention. Participants who consumed 200mg caffeine showed 20% higher recall rates.”
→细节题答案:200mg caffeine提升20%记忆留存。
🔸文学类文段:
❖关注作者对事件的评价词(如“flawed”“revolutionary”),快速判断态度。
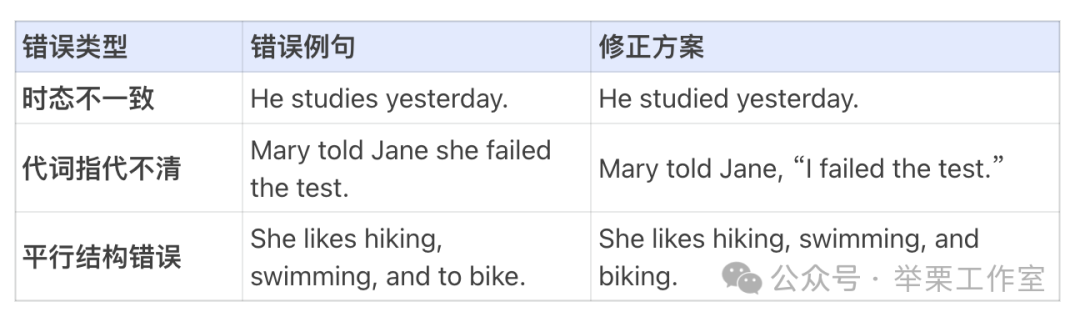
3. 文法陷阱:新增高频错误类型
三、综合提分策略:阶段化备考与资源整合
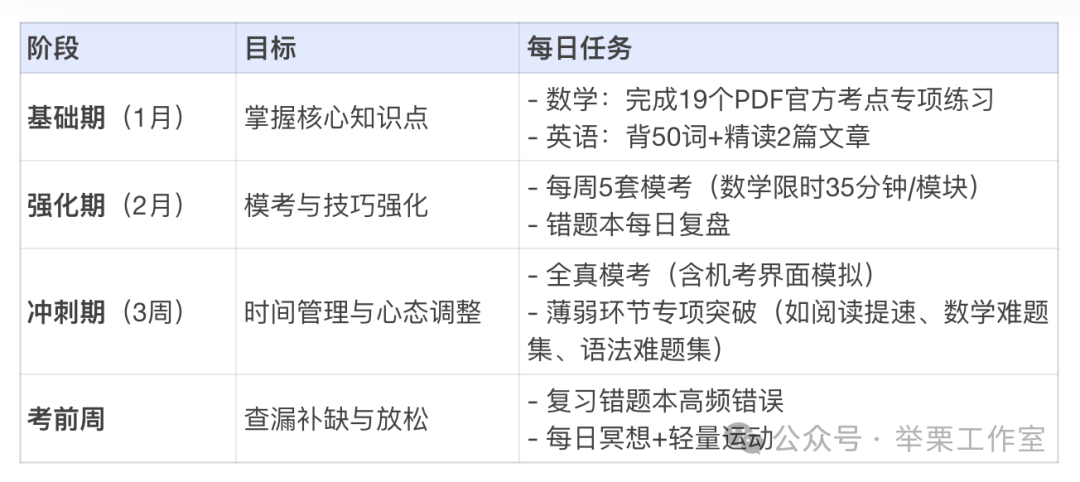
1. 四阶段备考计划表
2. 资源高效利用指南
🔸官方资源:
❖Bluebook机考平台:7套自适应题需至少刷3遍,分析每道题的考点分布。
❖ SAT官方指南:重点研究例题解析,总结出题逻辑。
🔸第三方工具:
❖UWorld:高难度阅读题可标记“陷阱选项”,整理常见干扰模式。
❖ Anki:创建动态词汇卡,利用间隔重复记忆法巩固学术词汇。
3. 考场终极技巧
🔸数学部分:
❖易因粗心丢分,完成后再花5分钟复查。
❖ 几何题无思路时,用Desmos绘制图形辅助分析。
🔸英语部分:
❖先做语法(16-27题),后做阅读(1-15题)。
❖ 12-15题难度较高,不要花太多时间。
🔸设备准备:
❖考前3天测试电脑续航与网络,准备备用设备。











