AMC美国数学竞赛的题型有哪些？

AMC（American Mathematics Competitions）是美国著名的数学竞赛，旨在激发学生对数学的兴趣和提升其解题能力。本文将深入探讨AMC竞赛的不同题型，帮助读者更好地理解这些题型的特点和解题策略。具体内容包括：1. AMC 8、10和12的不同之处；2. 选择题与填空题的分类；3. 数学概念在题目中的应用；4. 逻辑推理与图形问题；5. 实际应用问题解析；6. 难度分级与备考建议；7. 常见问题解答。通过对这些板块的分析，读者将能够全面了解AMC竞赛中的各种题型及其应对策略。

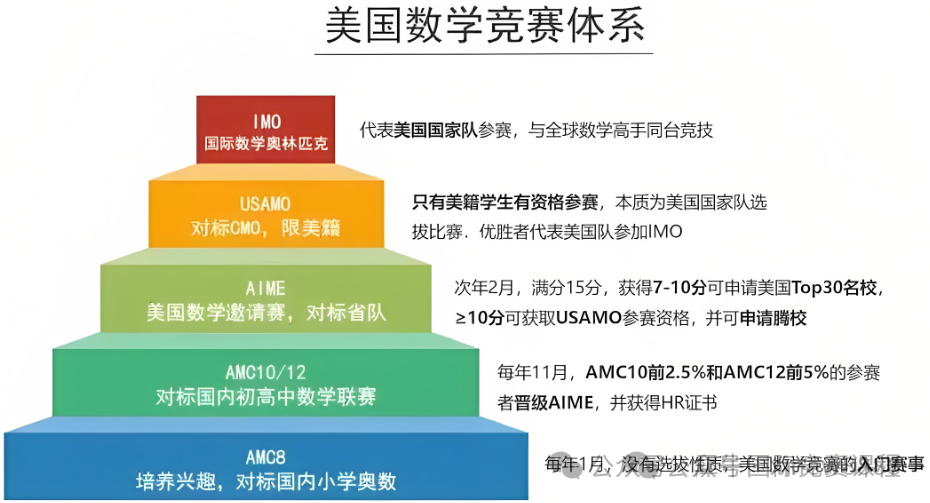
一、AMC 8、10和12的不同之处

AMC竞赛分为多个等级，其中最基础的是AMC 8，接着是AMC 10和AMC 12。这些比赛分别针对不同年级和能力水平的学生，因此在题目难度和知识要求上存在显著差异。

AMC 8

该比赛主要面向8年级及以下学生，难度相对较低，通常涉及基础数学概念，如算术、几何、代数等。每年考试时间为40分钟，共有25道选择题，每道题有5个选项。

AMC 10

针对10年级及以下学生，难度逐渐加大。考试时间同样为40分钟，但包含的问题更加复杂，需要运用更深入的代数与几何知识。总共也是25道选择题。

AMC 12

此项赛事适合12年级及以下学生，其难度最高。除了涉及更多高级数学知识外，还会包含一些组合数学和数论方面的问题。这部分同样设置为25道选择题，但考察范围更加广泛。

二、选择题与填空题的分类

在AMC比赛中，主要采用选择题形式，而后期的一些赛事如AIME则会引入填空题。这两种形式各有特点，对考生提出了不同要求。

选择题

每道选择题都有五个选项，其中只有一个是正确答案。考生需根据自己的判断作答，这种形式不仅测试学生对知识点的掌握程度，还考验其判断能力。例如，在一道几何问题中，如果考生能迅速排除明显错误选项，将大大提高答对率。

填空题

虽然在初期阶段不常见，但在后续赛事如AIME中，填空式问题开始出现。在这种类型的问题中，考生需要独立得出答案并填写，这要求更高的计算能力和逻辑思维。例如，在解决复杂方程时，可能需要多步计算才能得到最终答案，这就增加了挑战性。

三、数学概念在题目中的应用

AMC竞赛中的许多问题都涉及特定数学概念，例如算术运算、代数表达式以及几何性质等。这些概念不仅是解答问题所必需，也是构建解决方案的重要基础。

算术运算

基本算术运算如加法、减法、乘法和除法是解决许多简单问题的重要工具。例如，在求一个数列前n项之和时，通过掌握求和公式，可以快速得出结果，从而节省宝贵时间。

几何性质

几何问题通常涉及图形面积、体积以及角度计算等内容。在处理这些问题时，熟悉基本几何定理（如勾股定理）会极大提高解答效率。例如，在求解三角形面积时，可以利用底边与高之间的关系进行快速计算。

四、逻辑推理与图形问题

逻辑推理能力是成功应对AMC竞赛的重要因素之一。有些问题通过文字描述或图形展示，需要考生进行合理推理，以得出正确答案。

图形识别

许多几何问题以图形形式呈现，这要求考生具备良好的空间想象力。例如，通过观察图形特征，如边长比例或角度关系，可以得出相关结论，从而找到解决方案。在某些情况下，一个简单的小变化可能导致整体结构的大改变，因此细致观察至关重要。

推理技巧

逻辑推理不仅限于图形，也可以应用于文字描述的问题。在这类情况下，需要提取关键信息，并进行合理推断。例如，对于某个条件下成立或不成立的问题，通过建立假设并验证，可以有效缩小范围并找到正确答案。

五、实际应用问题解析

实际应用类的问题往往结合生活场景，让学生将所学知识运用到现实中去。这类问题不仅增加了趣味性，也提升了实用性，使得学习变得更加贴近生活。

财务管理

例如，在个人财务管理方面的问题中，可能会询问如何制定预算或计算利息。这类问题不仅需要掌握相关公式，还要理解其背后的经济原理，以便做出合理决策。同时，这也鼓励学生关注日常生活中的数学应用，提高他们解决实际问题的能力。

科技创新

科技领域的问题也越来越受到重视，比如如何利用数据分析优化资源配置。这类情境下，不仅要具备扎实的数据处理能力，还要能够运用统计学原理进行有效分析。因此，对这类综合性强的问题进行练习，有助于培养全方位思维能力，提高综合素质。

六、难度分级与备考建议

由于AMC比赛涵盖多个层次，因此对于不同水平的考生来说，应采取相应备考策略，以便有效提升成绩。同时，要根据自身情况灵活调整复习计划，以确保充分准备各类类型的问题。

难度划分

根据过去历届考试情况，可以将试卷划分为易、中、难三种类型。在复习过程中，应注重基础知识掌握，并逐步挑战更高难度的问题。此外，通过模拟考试来熟悉考试节奏，也是提升应试能力的重要方式之一。

定期自测

定期自测可以帮助考生了解自己的薄弱环节，从而有针对性地加强训练。可以通过历年的真題进行练习，同时参考优秀学长分享经验，总结出适合自己的复习方法。此外，与同伴组队讨论也是一种有效学习方式，通过交流彼此思路，共同进步，实现资源共享，提高整体学习效果。

七、常见问题解答Q&A

AMC比赛适合哪些年级的学生？
AMC比赛主要面向小学至高中阶段的学生。其中 AMC 8 针对8年级及以下，AMC 10 针对10年级及以下，而 AMC 12 则适合12年级及以下学生参与。因此，不同年龄段均可参与相应等级赛事以展示自己的数学才能。

如何准备AMC比赛？
准备工作可以从基础知识入手，加强对核心概念如代数、几何等领域内容的理解。同时，多做历年的真題练习，加深对不同类型问提风格及解法技巧认识。此外，与他人讨论也是一种很好的学习方式，有助于拓宽思路，提高解答效率.

参加AMO是否需要特别高超的数学技能？
虽然AMO（American Mathematics Olympiad）是一个竞争激烈的平台，但只要具备扎实基础并且愿意花时间进行训练，就能获得不错成绩。因此，无需过于担心，只要积极努力，就一定能够取得进步！