Bebras竞赛Year 11-13级别题目详解

准备好迎接脑力的终极考验了吗？Bebras竞赛Year 11-13级别的题目不仅仅是在考你对算法和数据结构的熟悉程度，更是在向你发出智力巅峰挑战！在这个阶段，简单的逻辑游戏已经不足以满足你的“烧脑”需求，现在是时候进入更高级别的智慧竞技场，面对复杂的算法、数据结构和计算机系统问题，真正体验成为一名计算机科学家的快感。PGA为你准备了这份详细的考点指南，让你在轻松有趣中掌握竞赛核心内容，化解每一个烧脑难题！

01、高级算法与数据结构(Advanced Algorithms and Data Structures)

树状结构与图论 (Tree Structures and Graph Theory):

题目展示了工厂生产流程的树状图结构，要求学习理解如何通过图论中的树结构来表示生产和包装单位之间的关系。这在数据结构的学习中非常重要，特别是涉及到树和图的表示与遍历。

流程优化与路径规划 (Process Optimization and Path Planning):

学生需要分析每个生产单位如何连接以及如何将产品送到最终的包装单位。这类似于路径规划和流程优化问题，在高级算法中应用广泛。

资源分配与依赖关系 (Resource Allocation and Dependency Relationships):

题目要求理解单位之间的依赖关系，即每个生产单位如何依赖于前一个单位，包装单位则作为流程的终端。这涉及到资源的分配和处理多个依赖关系的能力。

02、图论与网络优化(Graph Theory and Network Optimization)

最短路径问题 (Shortest Path Problem):

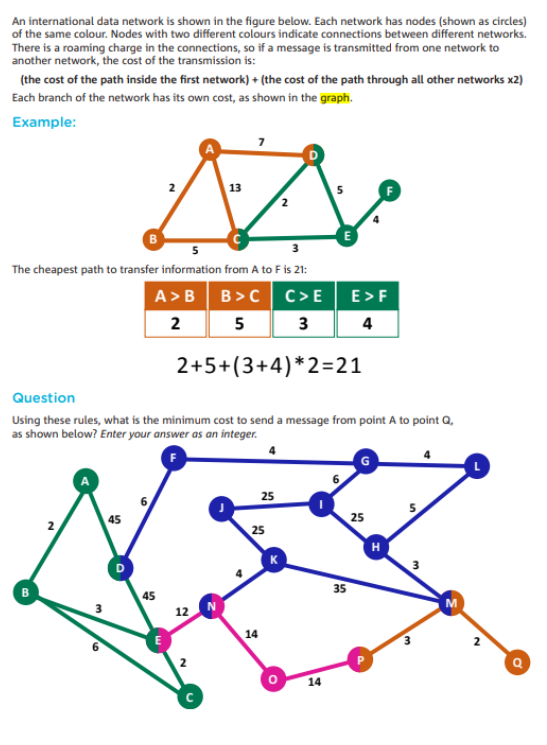
题目要求学生在一个图中找到从一个节点（A）到另一个节点（Q）的最小传输成本。这类似于图论中的最短路径问题，学生需要应用图的遍历算法来找到路径，并计算其对应的总成本。

网络传输成本计算 (Network Transmission Cost Calculation):

题目中每个网络的连接线都有不同的成本，且跨网络的传输费用是双倍的。学生需要掌握如何在图中根据边的权重计算路径成本，并特别注意跨网络的额外成本。

动态规划与路径优化 (Dynamic Programming and Path Optimization):

在求解最短路径的过程中，学生可以应用动态规划的思想，通过比较不同路径的成本来找到最优解。这是网络优化中的重要技术。

03、递归与动态规划(Recursion and Dynamic Programming)

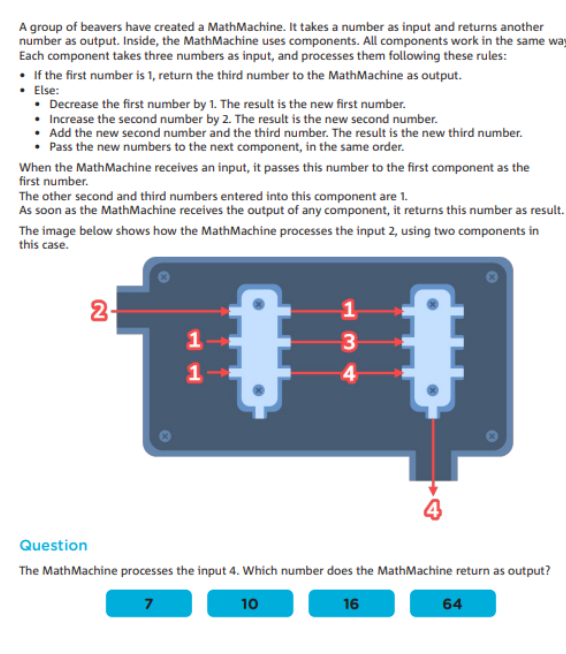
递归调用 (Recursive Calls):

题目中的 MathMachine 是一个递归结构，它根据输入值不断调用自身的组件，并最终输出一个结果。理解递归的工作方式对于解答这个题目至关重要。

状态转移与更新(State Transition and Updates):

每个组件对输入的数字进行状态转移，包括对数字的增加、减少和传递，这类似于动态规划中的状态更新。在递归调用的过程中，组件的状态发生变化，最终影响输出结果。

递归终止条件(Recursive Termination Condition):

题目明确了递归终止条件：当输入为 1 时，直接返回第三个数字。学生需要理解这一终止条件在递归过程中的作用。

04、计算机系统与并发编程(Computer Systems and Concurrent Programming)

顺序执行与结果预测 (Sequential Executionand Result Prediction):

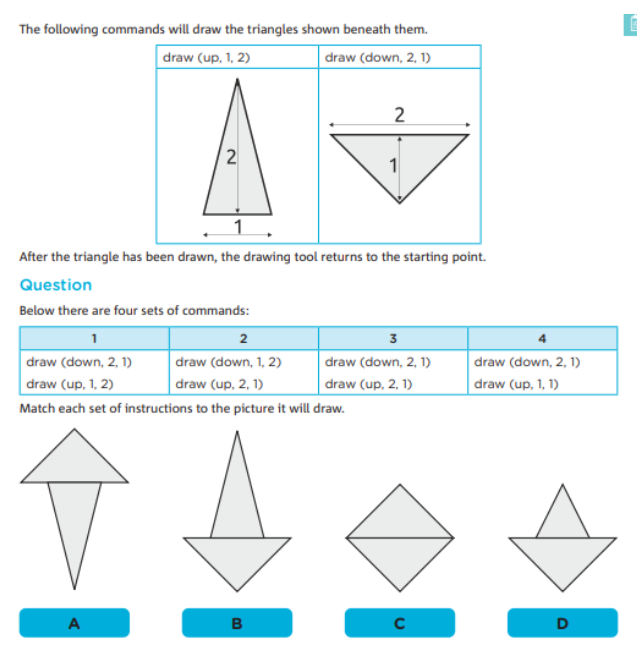
题目给出了一系列的命令，每个命令将绘制一个三角形。学生需要理解这些命令按顺序执行后所产生的图形，这涉及到计算机系统中的顺序执行和并发任务的顺序控制。

命令的重复与组合 (Repetition and Combination of Commands):

每组命令重复两次绘制三角形，然后回到起始点。学生需要根据命令的组合来预测最终的图形，这与编程中的循环和条件控制相似。

图形的对称性与变化 (Symmetry and Transformation of Shapes):

题目涉及到对图形的对称性和旋转的理解，通过绘制不同方向的三角形，学生需要识别最终的图形形状，这类似于图形编程中的坐标变换和图形处理。

05、组合数学与概率(Combinatorics and Probability)

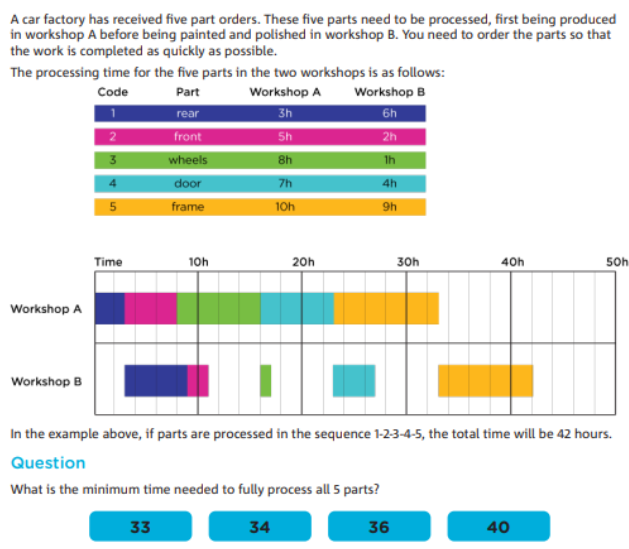
调度与排序 (Scheduling and Sequencing):

题目要求学生将不同的汽车零件的加工顺序进行优化，以确保总加工时间最短。这是一个经典的调度问题，属于组合数学中的排序与优化问题。

并行处理与资源优化(Parallel Processing and Resource Optimization):

由于两个车间需要并行处理不同的任务，学生需要考虑如何安排这些任务，以最小化整个过程的总时间。这涉及到资源的合理分配与利用，以实现时间的最小化。

排列组合(Permutations and Combinations):

学生需要考虑不同的排列组合，以确定哪一种排列方式能够使加工时间最短。

06、机器学习基础(Basics of Machine Learning)

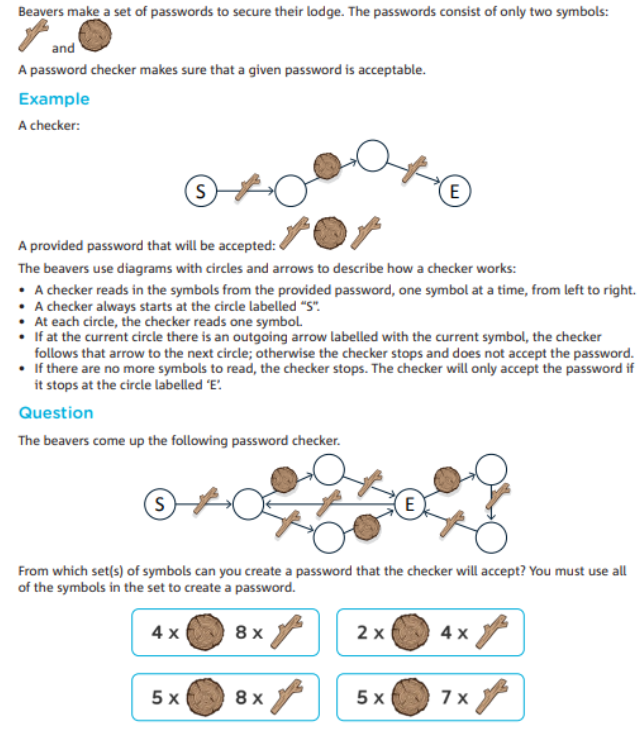
状态机与状态转换(State Machines and State Transitions):

题目中的密码检查器实际上是一个有限状态机 (Finite State Machine, FSM)，根据输入符号的不同进行状态转换。学生需要理解状态机的工作原理，特别是在不同输入情况下如何进行状态转换，以及如何判断最终状态。

路径识别与决策树(Path Recognition and Decision Trees):

题目中不同的路径代表了不同的符号序列，类似于决策树中的不同路径。学生需要识别哪些路径能够通过状态机并最终接受密码，这与机器学习中的路径选择和决策过程类似。

符号序列的生成与验证 (Sequence Generation and Validation):

学生需要生成符号序列并验证它们是否能够被状态机接受，这类似于在机器学习中生成并验证特征序列的过程，以确保最终结果符合期望。

07、密码学与信息安全(Cryptography and Information Security)

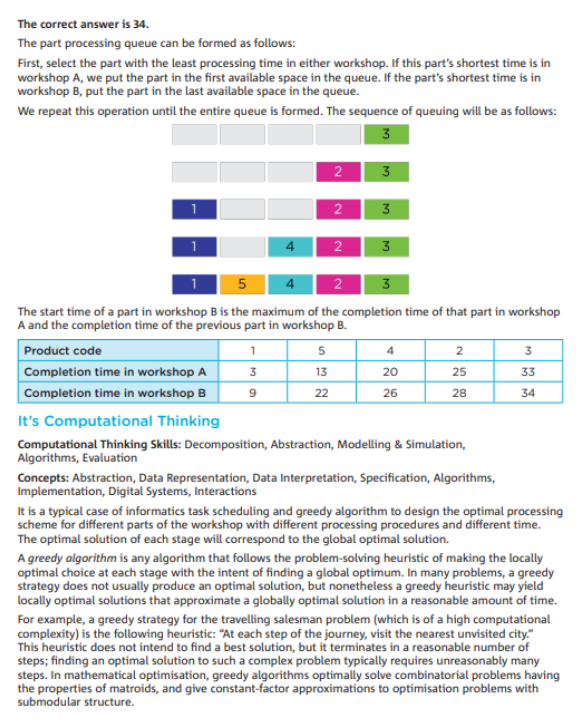
算法的抽象与建模 (Abstraction and Modeling of Algorithms):

题目涉及到如何有效地排列和调度零件的加工顺序，这是一个优化问题。在密码学中，优化算法用于加密过程的效率提升。通过对问题的抽象和建模，可以找到最佳的处理顺序。

贪心算法 (Greedy Algorithm):

题目中使用了贪心算法来安排零件的加工顺序，确保每一步选择都朝着最小化总时间的方向前进。贪心算法在密码学中常用于简化计算过程和快速找到次优解。

数据表示与处理 (Data Representation and Processing):

数据表示和处理的方式在信息安全中非常重要，尤其是在优化算法中。如何有效地表示和处理时间数据，决定了最终结果的准确性和有效性。

总结

在Bebras竞赛Year 11-13级别的挑战中，每一个考点都是对你智力的极限挑战，而PGA的课程将帮助你一步步征服这些挑战。无论是高级算法、图论，还是机器学习和密码学，我们将带你深入浅出地掌握每一个知识点，让你在竞赛中游刃有余，轻松取胜。加入PGA课程，踏上这段充满挑战与乐趣的竞赛之旅，让你的计算思维和问题解决能力达到新的高度！