Edexcel考试Further Math高数备考指南

{Edexcel}高数不完全备考指南

随着国内疫情的发酵，部分地区AQA, CIE已经取消了今年的考试，改为POE；而在这之中，Edexcel依然坚持考试；今天老师就来带大家看一看Further Math部分的内容。

因为今年整体疫情的原因，官方发布了advance information, 旨在帮助学生缩小考试范围，而这份资料中又能看出很多今年题型的端倪，因为高数是大题制，并没有选择等小问题，因此没有罗列的内容都基本就不会考了。

Core Pure Math paper 1 & 2

[斜体带下划线的为Paper 2]

LOOK01

Ø Complex number

1. Complex numbers: Multiplication and division, conjugates → 标准形式的乘法与除法

2. Complex numbers: Roots of polynomial equations, Argand diagram → 3次/4次方程的复数解，在复平面表示不同的复数。

3. Complex numbers: Multiplication and division → 三角形式的乘法与除法

4. Complex numbers; Addition and subtraction; simple loci in the Argand diagram → 复平面的类似几何问题

   复数部分历来都是考试的重点，但是从考试的内容来看不会是今年的难点；复数与指数结合的难点并不会考。考试题型基本如下：

LOOK02

Ø Matrix

1. Matrices: Inverse of a 3 × 3 matrix, singular and non-singular → 给定系数k，求三维矩阵的逆矩阵

2. Use matrices to represent linear transformations in 2-D → 二维平面的transformation，尤其是先后两次transformation的合并计算

3. Matrices: Solution of three simultaneous equations → 通过三维逆矩阵求三元方程的解，以及解释平面关

   Matrix部分的题型非常清楚，一定要多练习呀！

考试题型基本如下：

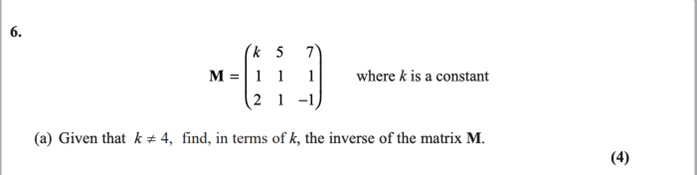
LOOK03

Ø Calculus

1. Volumes of revolution → 绕x轴，y轴求积分，注意隐藏的圆锥和圆柱的加减

2. Improper integrals → 反常积分，注意断点和步骤的规范化

3. Partial fraction integration → 裂项求积分，注意ln, arctan, x^(-2)不同的形式

4. Differentiate inverse trig function → 复杂反三角函数的微分

5. Differentiate hyperbolic function → 双曲函数的微分

6. Maclaurin series → 泰勒级数展开

微积分部分一直都是重点，要对所有函数形式的微分和积分有了解，尤其是要会推导三角，反三角，双曲，反双曲函数的微分和积分。

考试题型如下：

LOOK04Ø Others

1. Difference for summation of finite series → 裂项求级数和，尤其注意n, n^, n^3的形式

2. First/Second order differential equation → 微分方程

3. Induction → 数学归纳法，注意四类题型

4. Vectors→ 空间几何，注意线和面的向量表示，夹角的求法以及点到平面的距离

5. Polar coordinates → 极坐标，注意切线的x，y关系，以及包裹面积的加减可能性

paper1 的难点依然会停留在微分方程的运算上，除了背下不同形式下的通解外，一定要有对解再次微分求极值的想法；

paper2 的难点会在极坐标上，不同样貌的常见的螺线大家要多加掌握。

以上就是老师分享edexcel考试高数的总结。