AMC 12 的几何定理比 AMC 10 难了多少？

咱们介绍 5 个 AMC 12 几何板块中需要滚瓜烂熟的公式定理：

1.海伦公式 （Heron's formula）

2 维维亚尼定理 （Viviani's Theorem）

3 托勒密定理 （Ptolemy's Theorem）

4 圆幂定理 （The Power of a Point Theorem）

5.倍角公式

1海伦公式（Heron's formula）

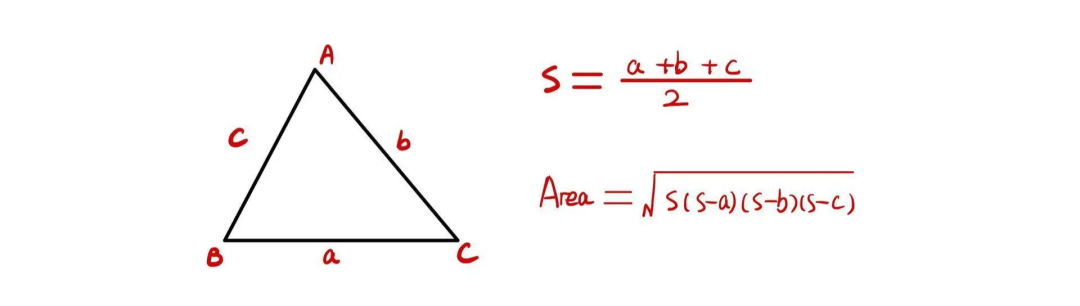
这个公式是一个求三角形面积的“万能公式”，基本上对于所有和三角形面积相关类型的题目，都可以尝试着使用这一公式去求解。

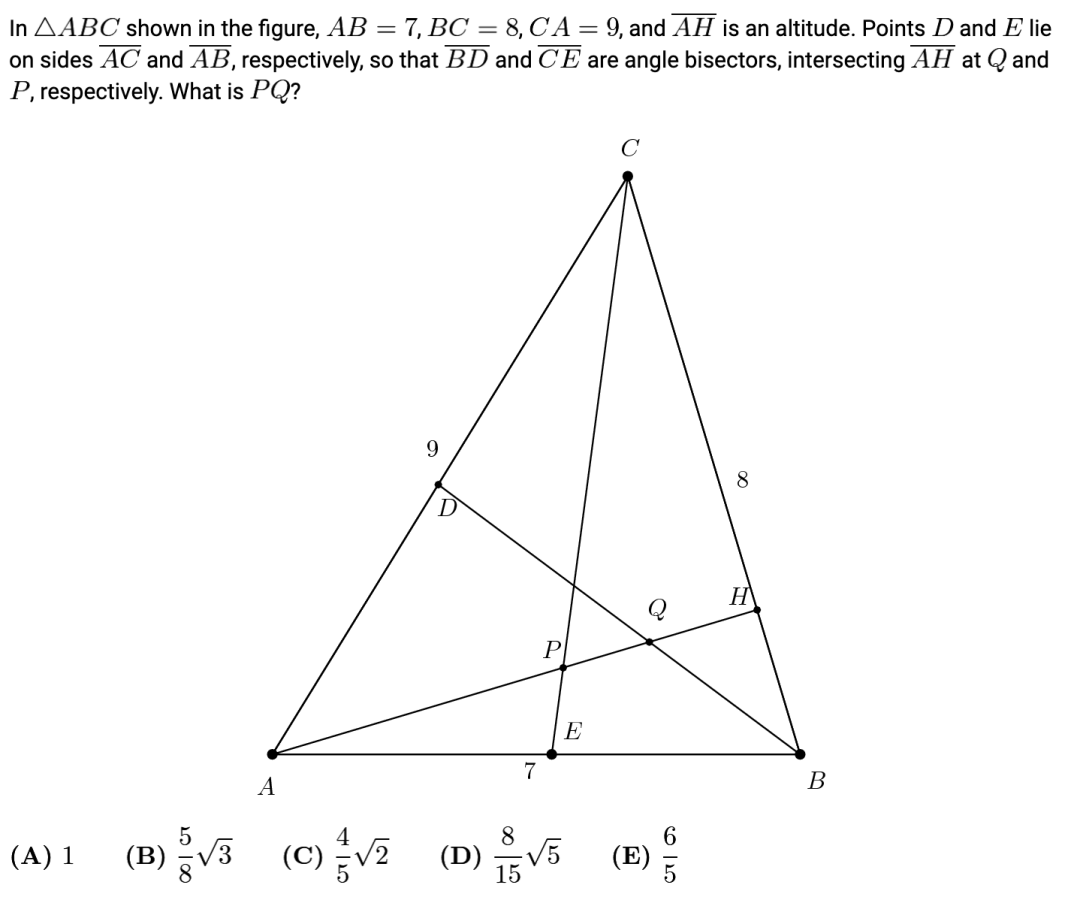
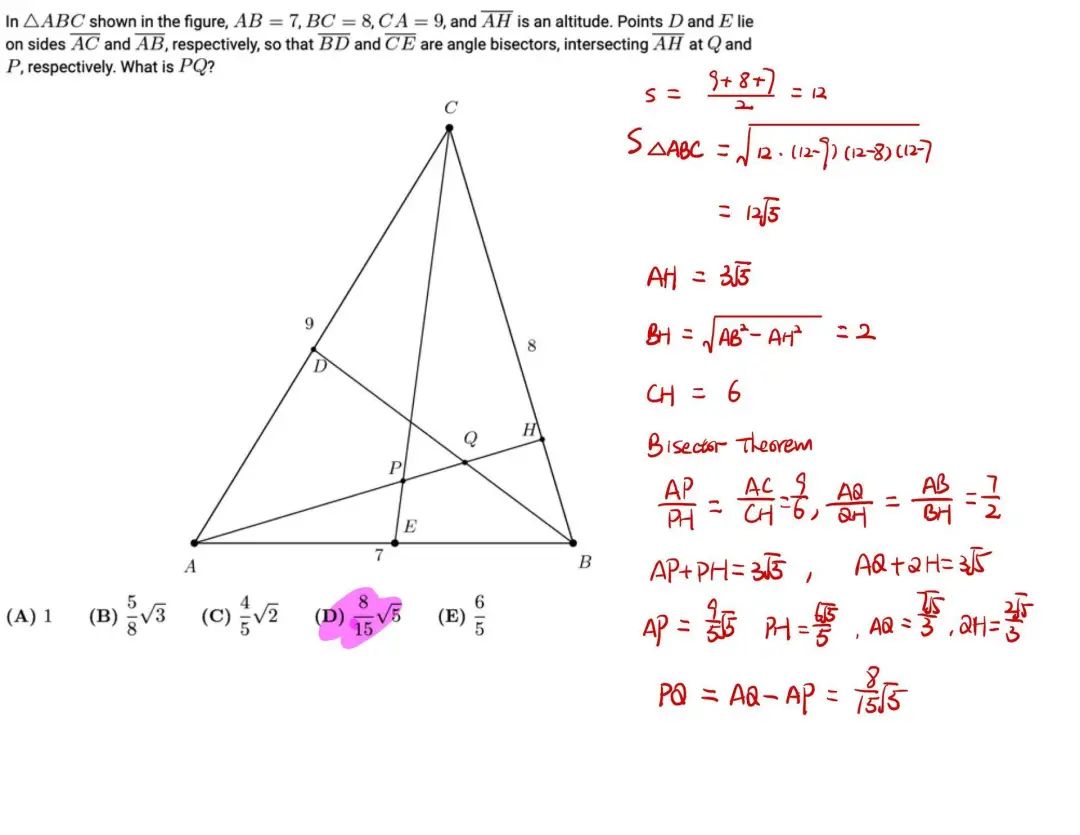
下面这道例题不仅要用到海伦公式，还需要在 AMC 10 中已经讲解过的角平分线定理。

AMC12B 2016 Q17 （答案见最后）

2、维维亚尼定理

（Viviani's Theorem）

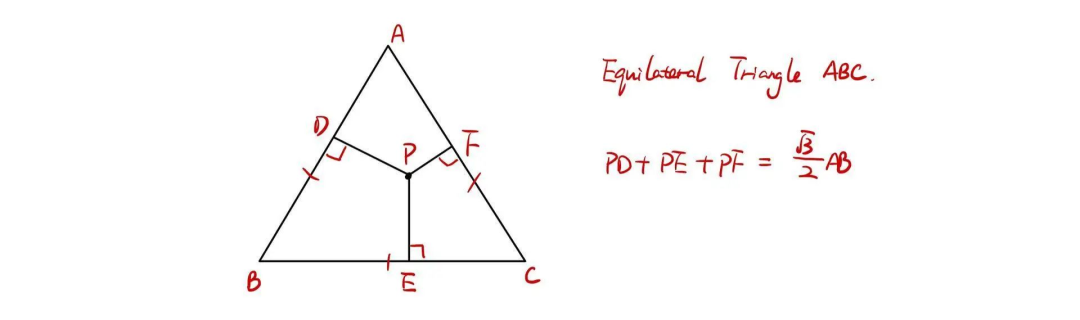
针对等边三角形作为已知条件，维维亚尼定理给出来三角形内一点到三条边距离的代数关系。这一定理很适合用于求解等边三角形的边长。

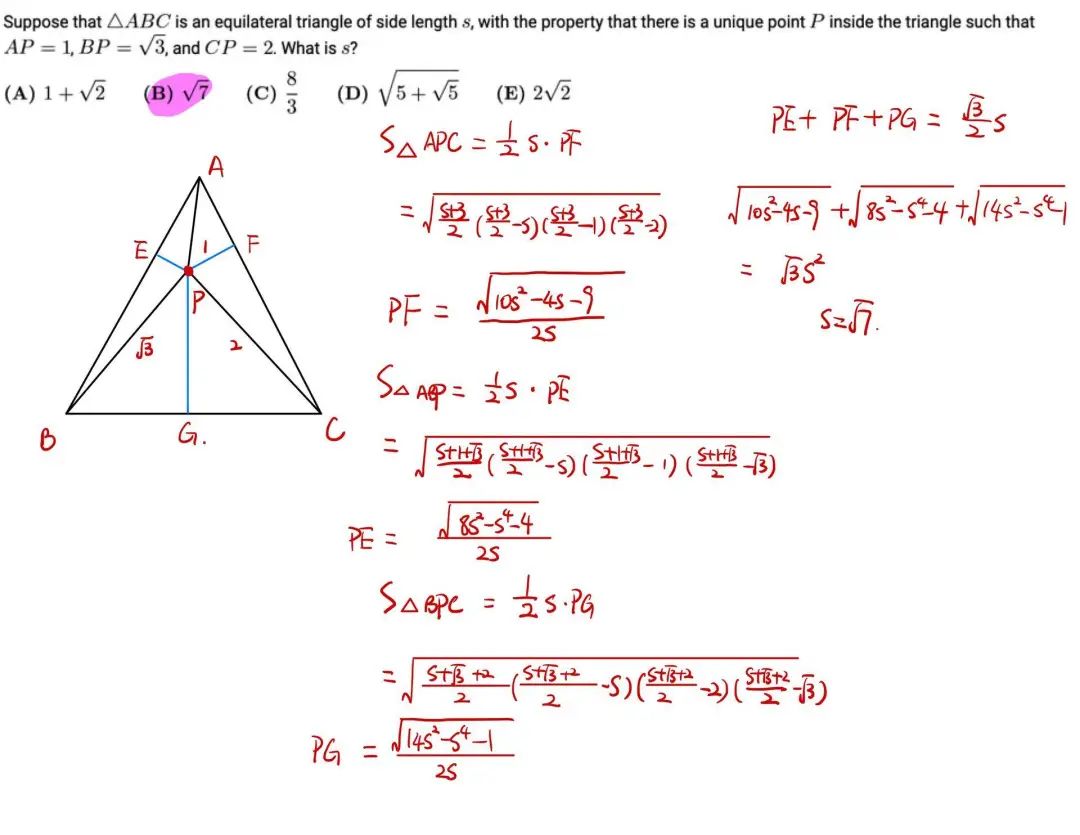
例如下面这道题需要同时应用海伦公式和维维亚尼定理。

AMC12A 2020 Q24 （答案见最后）

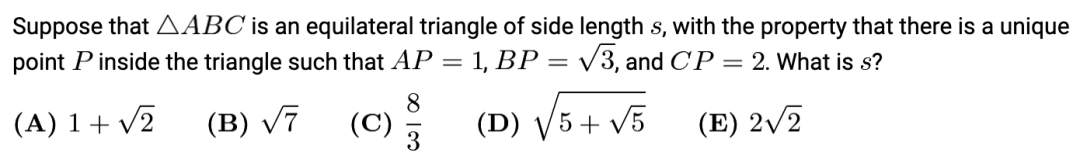
除了涉及三角形及多边形，相比于 AMC 10, AMC 12 中还有会出现以圆为考察点的题目。

关于圆的内容是整个中学阶段涉及相对较少的部分，针对这一类题目，掌握一些和圆相关的几何定理能够帮助我们更有效地打开解题思路。

3托勒密定理（Ptolemy's Theorem）

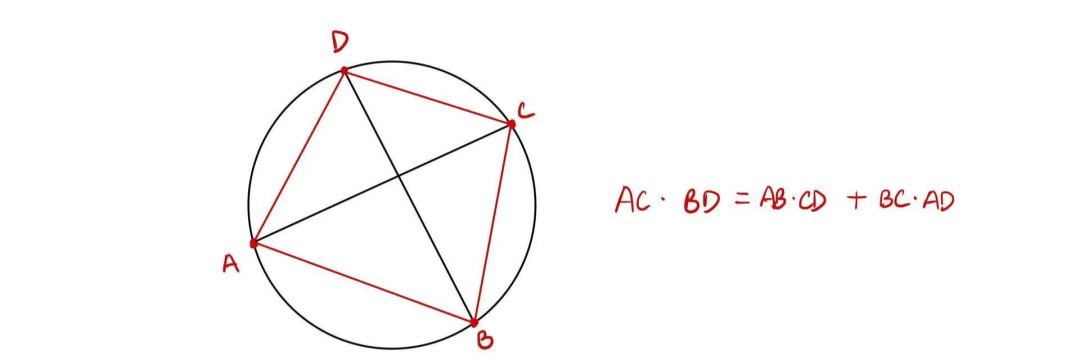
没错，这个定理是由传说中的那个古希腊天文学和数学家托勒密发现的。

使用这个定理有一个先决条件，一定别忘了要先证明四边形内接于一个圆。

下面这道例题在 AMC 12 的考试中是没有给出例图的，不知道你能不能找出哪四个点是内接于同一个圆的呢？

AMC12A 2018 Q20（答案见最后）

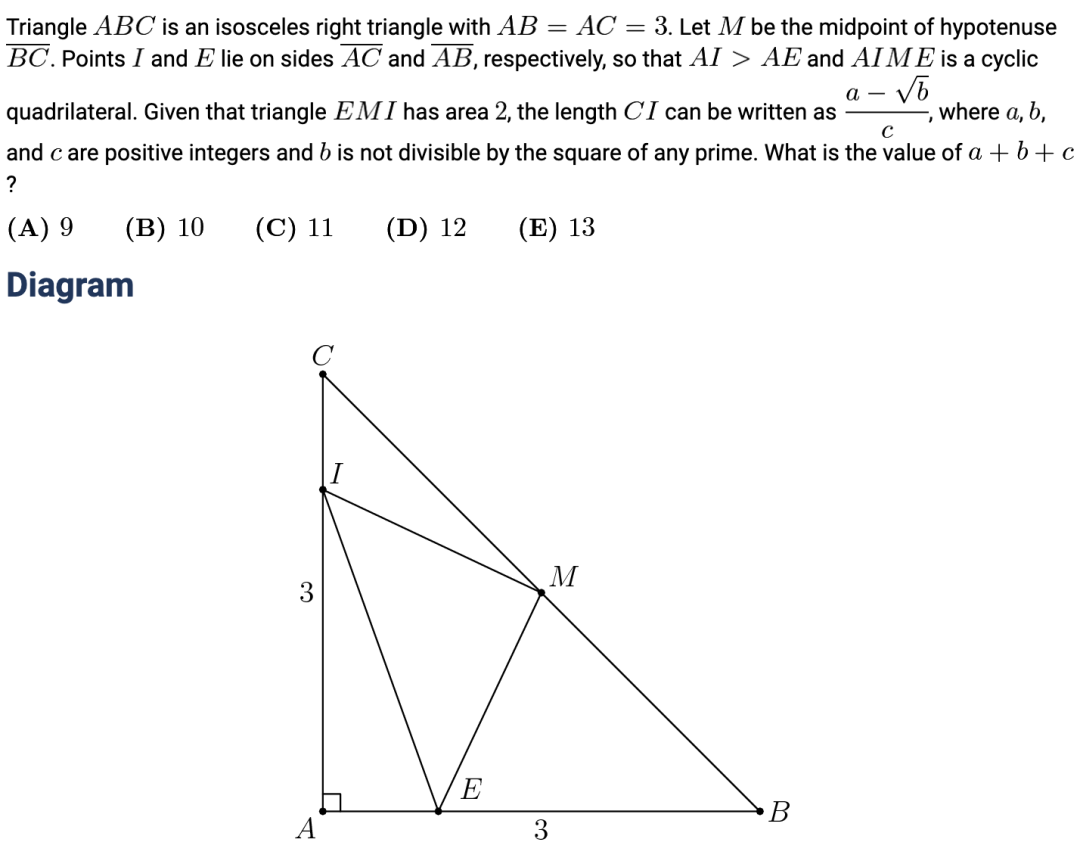
4、圆幂定理

（The Power of a Point Theorem）

关于这个定理，我只想说它真的不止是一个定理。完整的圆幂定理其实包含了三个部分：切割线定理 (The tangent-secant theorem)，割线定理 (Intersecting Secants Theorem)，相交弦定理（The Intersecting Chords Theorem）。

切割线定理 (The tangent-secant theorem)

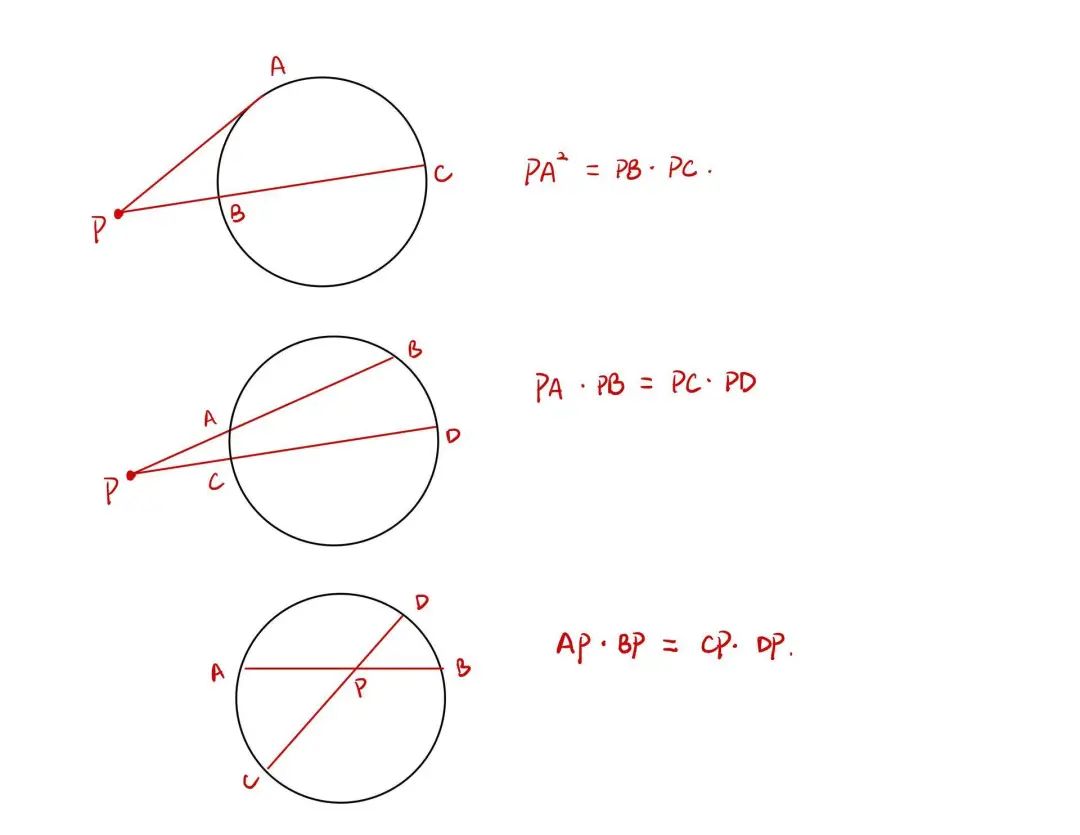
割线定理 (Intersecting Secants Theorem)

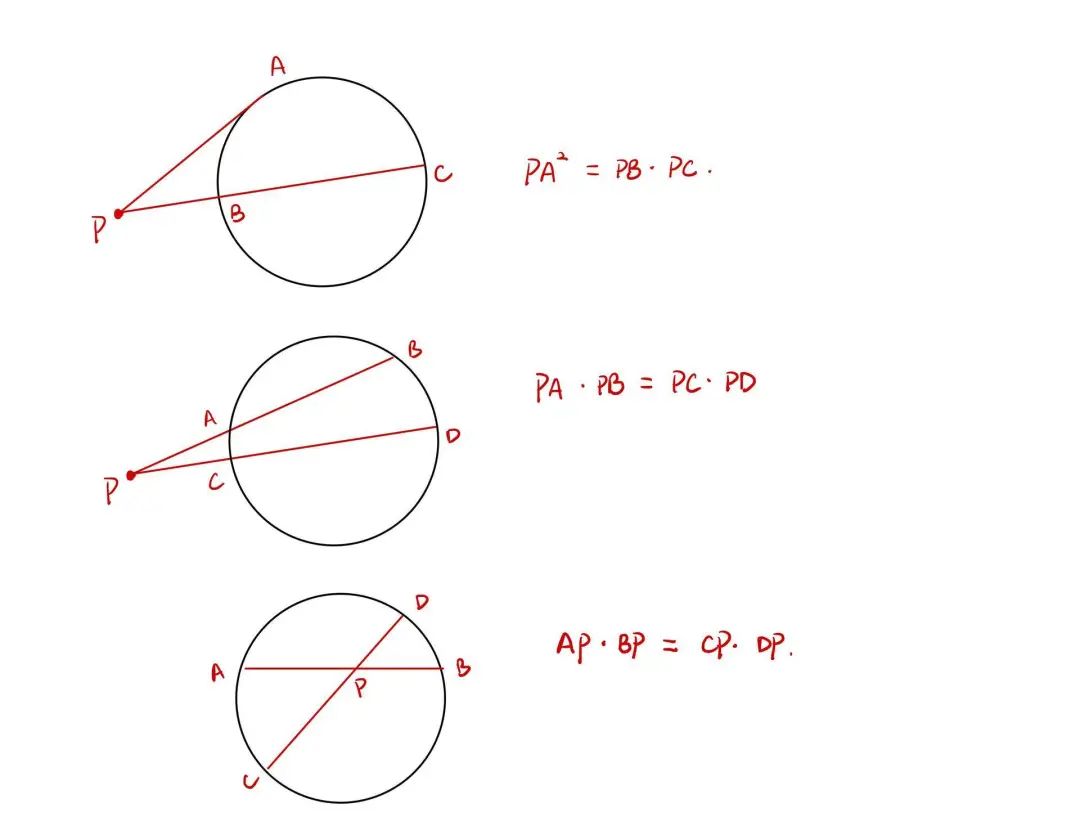
相交弦定理（The Intersecting Chords Theorem）

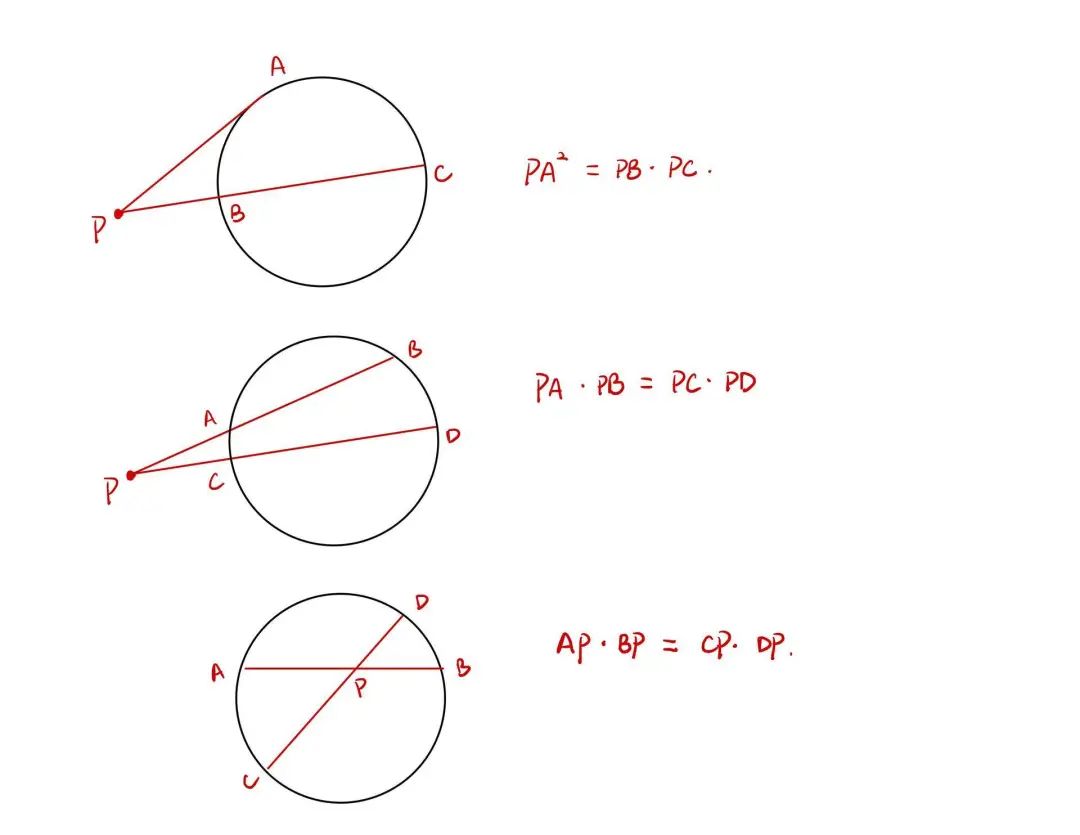
总结该定理的特点就是圆外或圆内一点到圆上两点距离的乘积（或切线长的平方）是一个定值。

下面这道题，大家看过之后有没有什么思路呢？

AMC12A 2017 Q24（答案见最后）

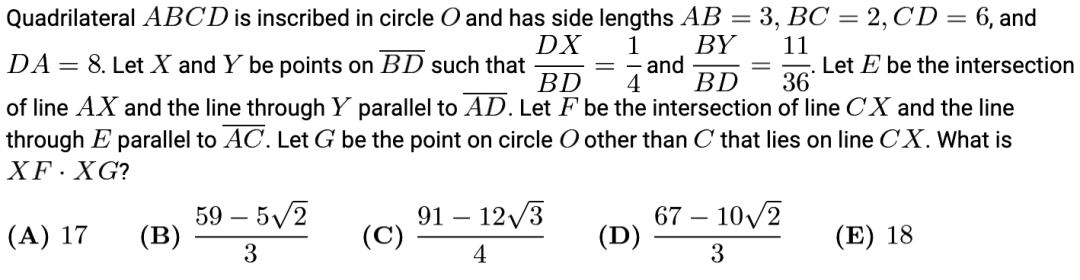
详细过程及答案

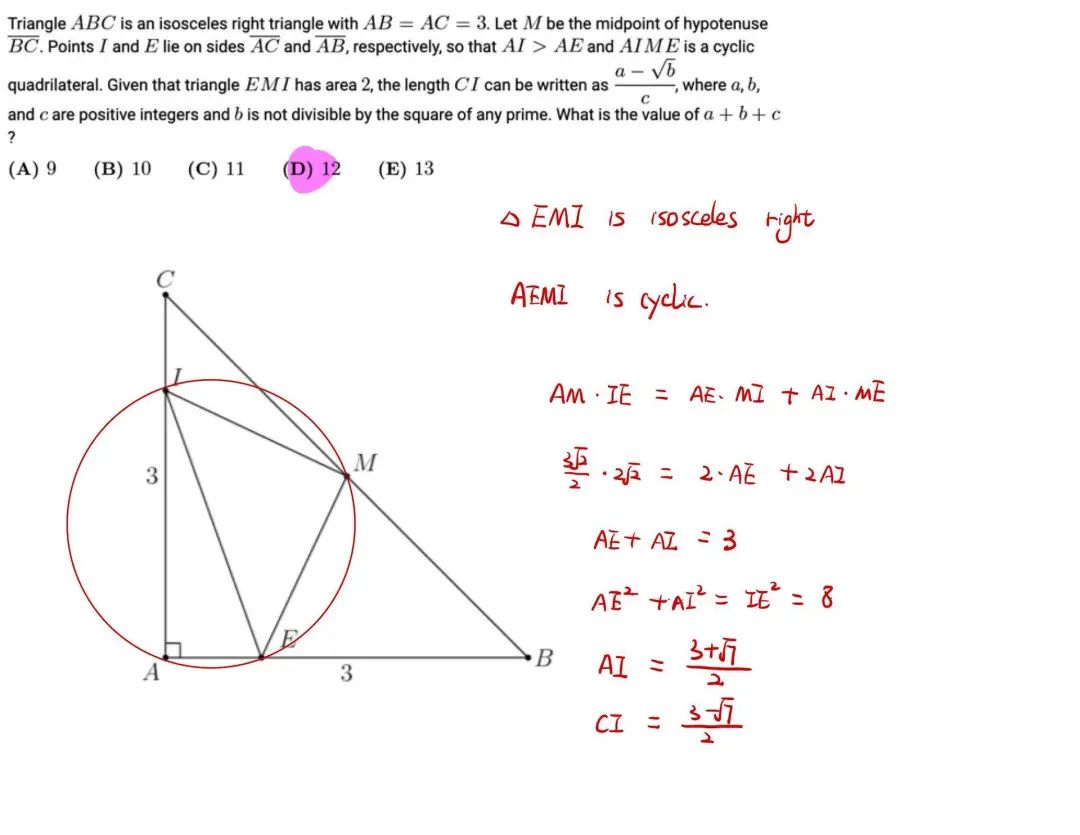
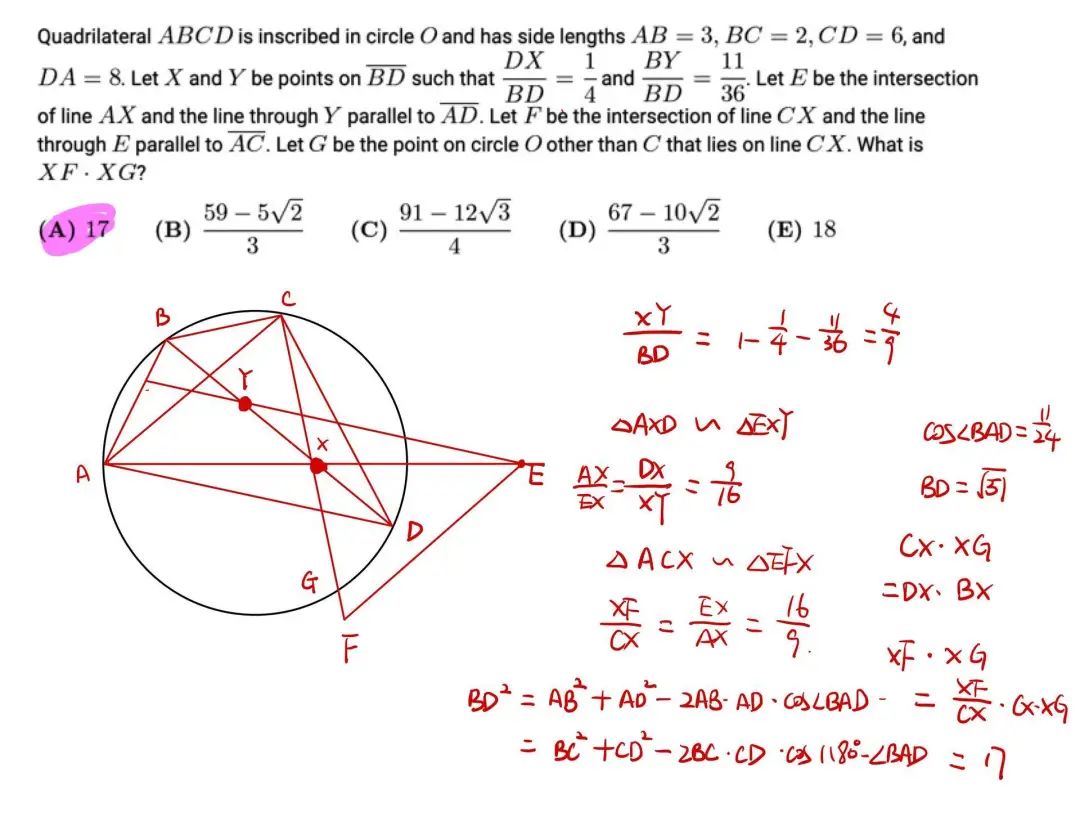
5、倍角公式