贝赛思Q1保姆级攻略来啦！数学首场Benchmark考试如何准备？

一转眼贝赛思第一个学季就要结束了，各核心科目的Q1 Benchmark考试预计在10月中下旬陆续进行，学科复习也可以准备起来了。

特别是数学，在超前学习、螺旋式上升、分层教学的特点下，经常有孩子感觉越学越难。而且数学作为其他理科学习的基础，在解决物化生的实际问题时提供了数学计算及相关数学方法的支持。因此，学好数学至关重要。

今天，机构理科教学组团队给大家带来贝赛思数学Q1的保姆级攻略，帮助孩子有针对性地准备Q1考试，冲刺拿到高分！

核心考点梳理归纳夯实数学基本功

在复习阶段，学生可以一边回顾Q1学季的知识点，一边查漏补缺，这也是为知识的系统化、能力化做好准备。每个年级的复习重点，当然都是在课堂上讲过了的，需要同学们从头到尾复习一遍。贝赛思在考前一周也会发放一份复习指南（含各科目的考察范围），大家可以充分利用，提高复习效率。

关于各年级该复习的重点，机构理科教学组团队也梳理归纳好了。

G3

四位以内整数读写，三位数以内加减法，分数基础知识，长方形/正方形的周长、面积计算，美元文字题等。

G4

三位数以内整数运算，同分母分数加减法，小数四则运算，因数与倍数，四则运算文字题等。

G5

多位整数的读写，分数四则运算，质因数分解，平方与开平方，四则运算/平均数文字题等。

G6

整数混合运算，小数运算，分数运算，求最大公因数与最小公倍数，代数式代入求值，单位换算等。

G7

正负数混合计算，绝对值与相反数，质因数分解(用指数表示结果)，解方程，占比文字题，体积/表面积计算等。

G8

相似三角形，圆内角度关系，勾股定理，连续整数/运动学文字题，解一元一次方程，解一元二次方程等。

预备微积分A

指数化简，科学记数法，坐标几何基础公式，复数，函数基础性质，十二种母函数图像，函数的复合等。

预备微积分AB

复数，解方程与不等式，函数的复合，反函数，函数图像变换，多项式函数，分式函数等。

预备微积分B

指数函数，对数函数，指数与对数模型，指数与对数方程与不等式，三角函数图像，解三角函数方程等。

经典题型拆解提高实战能力

在精准掌握了考点之后，紧接着就是要把出题模式搞清楚，这就是我们所说的典型题法则，遵循这一法则，同学们在平时的学习过程中会更加高效轻松，特别是在数学、物化生这样的理科。

以下列举了各年级的经典题型，涵盖考点分析及答案解析，大家可以自查一下，看看知识点掌握情况如何。

G3

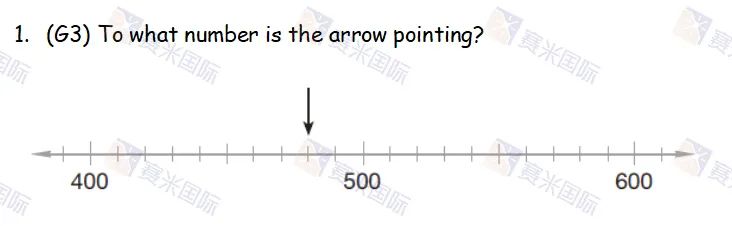
考点分析：考察学生对数轴的理解。

答案解析：在解题时要先找到参照刻度(500)，再计算该数轴每小格代表的数值(400到500间共有10小格，所以每小格代表100÷10=10)。箭头指的位置在500左侧2小格处，故数值为480。

G4

考点分析：考察四则运算的常用表述和学生的基础计算能力。

答案解析：在解题时先找到题目涉及运算的结构 “the sum is subtracted from the product”，其含义为从两数之积中减去两数之和，所以列式为20×10-(20+10)化简后为200-30，答案为170。

G5

考点分析：考察等值分数的判断。

解题思路：在求解时可以先尝试对各分数进行约分化简，再比对哪个分数的最简形式与其他分数不同，化简后可知前5个分数均可化简为2/3，而最后一个分数无法约分，最简形式即为28/45，故本题答案为28/45。

G6

考点分析：考察求三个较大数字的最小公倍数。

答案解析：题目已给出他们的质因数分解形式，因此只需先找到这些数字包含哪些不同的质因数(本题为2,3,5,7)，再寻找单个数字中每个质因数出现次数最多为几次(即每个质因子的最高次方，本题中2为4次，3为2次，5为1次，7为2次)，故最小公倍数为2⁴•3²•5¹•7²=35280。

G7

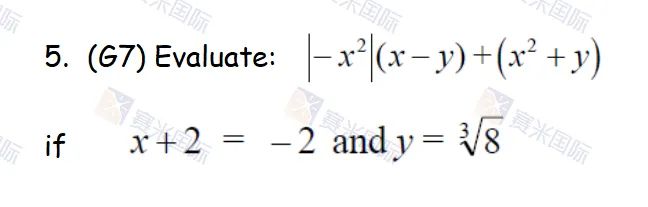
考点分析：考察代数式代入求值及正负数混合运算。

答案解析：在代入前要先化简算出x和y的值(x为-4, y为2)，再进行代入，代入过程中一定要记得在平方运算中x作为底数要包在括号内，代入后的算式为

|-(-4)²|(-4-2)+((-4)²+2)

计算可得最终结果为-78。

+

G8

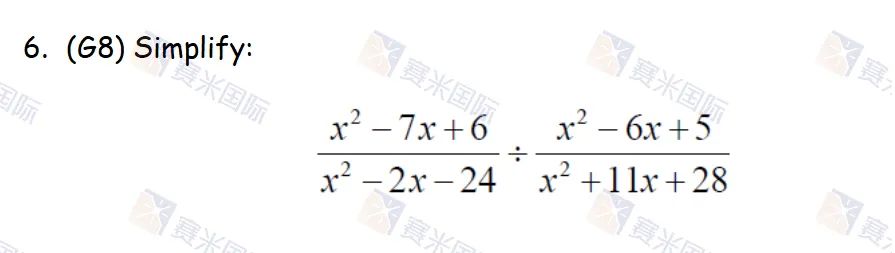
考点分析：考察分式除法。

答案解析：在进行计算前需要先对两个分式的分子分母进行因式分解，再利用倒数化除为乘并约分掉分子分母的公因式，最后把分子分母剩余的因式分别相乘。

PreCal A

考点分析：本题涵盖知识点较多，包含解二次不等式，不等式的图像表示，及集合的区间表示法。

答案解析：在求解时首先把所有项移到不等号的一侧，并把x²项系数化为正数，可得x²+7x+12>0

十字相乘后得(x+3)(x+4)>0

借助二次函数y=(x+3)(x+4)的图像可得y＞0时x的范围为x<-4或x>-3, 即口诀中的“大于取两边”。

图像表示为数轴上表示-4的点左侧及表示-3的点右侧两段射线的所有点(不包含两个端点-4和-3。

区间表示的答案为(-∞,-4)U(-3,∞)。

PreCal AB

考点分析：考察多项式函数的因式分解。

答案解析：常规的入手思路是利用有理根定理找到潜在的有理根，再通过代入求值找到第一个有理根，之后借助综合除法和二项式的因式分解来完成求解。但通过观察可发现本题可直接利用分组分解法入手：

PreCal B

考点分析：考察指对互逆的关系和反函数的求解。

解题思路：在解题过程中可采用老师在课堂强调的四步法(化f(x)为y,对调x和y，解出新的y，化y为f^-1(x))，其中在第三步需要用10为底数的指数来抵消掉log，大致步骤如下：

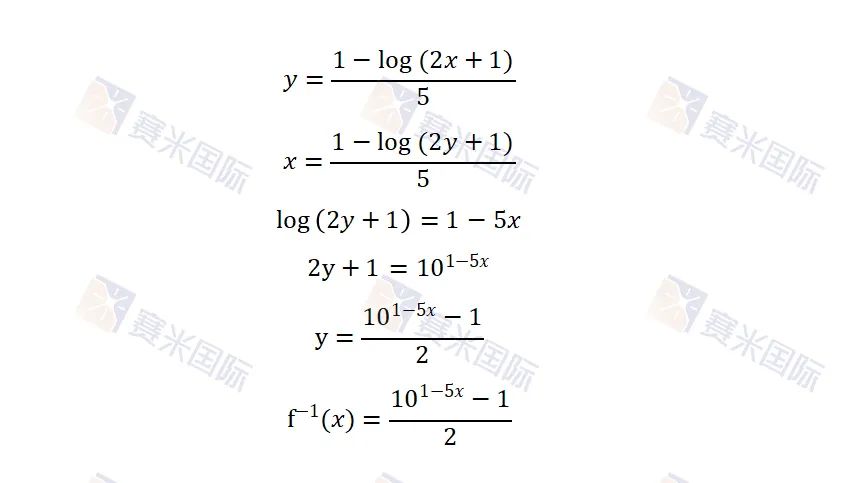
“笔记+错题”学思结合高效应考的两大法宝

最后想强调的是，课堂笔记和错题总结是学生在学习过程中两个不可缺少的重要环节，不仅是高效应考的两大关键，也是培养自主学习的有效途径。

回归课堂笔记

学生需要根据考试范围，结合笔记上的课堂同步内容进行针对性复习，重点关注不熟悉的知识点、公式以及常考题型。

错题总结

学生可以根据每次完成的课后练习总结易错题型，结合对应笔记进行整理归纳，存疑部分要及时解决；每次小测的主要丢分点也要重点关注。