距离第41届全国中学物理竞赛决赛已经过了一段时间。这段时间里我们也看到很多老师和竞赛大佬对本届试题进行点评和分析。
不过现有分析更多地是“就题论题”,分析思路、考点或模型,鲜有针对题目深度溯源,分析题目背景和命题思路的内容;尤其是针对多数人的易错点和未来的学习建议更是少之又少。
因此,我们特针对本次决赛理论试题进行深度拆解,对每道题目追根溯源,从命题的角度来分析同学们的“得”与“失”,并给予同学们最良心的学习建议。
话不多说,一起来看!
第一题
第一题围绕原子核的β衰变现象展开,这是一个经典的核物理现象。题目通过的β衰变展开,要求学生从不同角度分析该过程中的能量分布、动量守恒和角动量等基本物理过程,以及推断出由此产生的其他粒子的特征。
问题背景
β衰变的发现可以追溯到20世纪早期,科学家们通过实验发现某些原子核会自发地释放出电子,这些电子的动能分布呈连续状,而非预期的离散能级。这个现象在当时引发了广泛的争论,直到1930年泡利假设中微子存在。
泡利预言,原子核在β衰变过程中,在放出了β粒子的同时,还放出一个自旋为1/2,不带电荷、静止质量几乎为零的粒子。不久,费米将这种粒子命名为中微子。中微子假说成功解释了β衰变过程中的能量守恒和角动量守恒问题。
问题溯源
该题目源于大学核物理教材中的经典问题,同时结合了β衰变过程中粒子产生和能量分布的实验数据。在现代核物理或者粒子物理学导论等相关书籍中有较为详细的讨论,例如陈伯显的《核辐射物理及探测学》一书。
机构刷题营中也曾考查过β衰变的能量特性,讨论了β稳定核,即不会自发发生β衰变的原子核的特征。


该书是机构教研团队命题常用参考书籍


机构刷题营试题题目简评题目涵盖β衰变的多个方面,包括能量分布、动量守恒及角动量守恒。每个小问由浅入深,最后导向对未观测粒子的性质推测,考验学生的推理能力。核反应问题在CPhO中考试中并不是第一次出现,传统题目更倾向于考查能量、动量以及电荷守恒层面,而类似(4)中对于反应前后角动量守恒的考查是首次被搬上历史舞台。
从得分情况来看,这道题得分率并不高,大部分学生得分在23~26分区间,为什么看似简单的一道题,大家很难拿到30+?其原因是第一问不少同学把原子的静止质量Mp当作了原子核质量,同时(1)中题干的描述和引导做到不够精准,导致学生出现了非物理或者数学层面的错误。
当然,你可以吐槽出题人不了解竞赛或者大声高呼“史史史史史……”这并不能作为对未来命题风格和趋势预判的参考。那么这个问题给予我们怎样的启示呢?
首先我们一定要跳出刷题带来的惯性思维,翻阅近几年市面上模拟题,确实存在部分题目把原子质量作为原子核质量来处理的,如果保留了这样的惯性,在面对新题时是不利的,因为命题人可能直接以专业书籍或者论文作为依据和参考;其二,除了大量刷题外,养成阅读专业物理书籍的习惯也是必要的。
第二题
第二题主要研究一维耦合弹簧振子系统,这是物理学中研究波和振动的一个经典模型。在德拜的特殊模型中,振动模具有波的形式,实际上,振动模具有波的形式是晶格振动的普遍性质,这种振动模被称为格波。双原子链的格波模型的解较为简单,同时能全面地表现格波的基本特点。
可以看到存在两种不同的色散关系,即同相振动的低频支和反相振动的高频支,这两种振动模式就是所谓声学声子和光学声子,或许这是命题人选择该模型的原因。另外,固体物理中常选择的波函数周期性边条件,在本题中也采用了环状排列的模型做简单处理,而不涉及其量子力学本质,这一点的处理和复赛第七题是一致的。
问题溯源
《固体物理学 重排本 黄昆》书中P90-93讨论了双原子链的振动。同时再推荐两本书籍《固体物理学基础 阎守胜》以及《固体物理学导论 基泰尔》。
题目简评
题目分为多个小问,从振动方程的建立到本征模式和频率的求解,再到振幅、动能及频率的关系,逐步深入。
每一步都要求学生在前一问的基础上做进一步推导,考查了学生的逻辑思维和逐步求解复杂问题的能力。该题帮助学生理解了在复杂系统中不同振动模式的形成原因及其物理意义,这种设计可以引导学生将微观分析和宏观系统的特性结合。
通过变换条件(如锁定珠子、改变质量等),学生能更深入地理解振动系统的普遍规律和边界效应的影响。这种多层次的设问不仅是力学知识的考查,也是对学生物理模型建构和简化能力的训练。
值得一提的是,机构从21年刷题营至今,关于耦合弹簧振子系统的考查一直没有停过。
 机构刷题营模拟题
机构刷题营模拟题

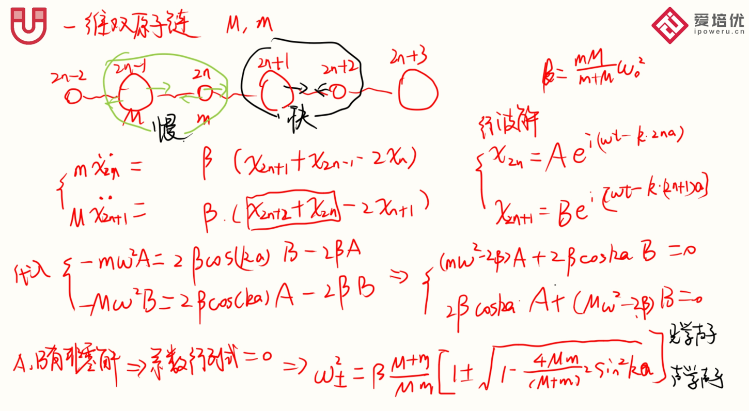
2024复赛刷题营板书
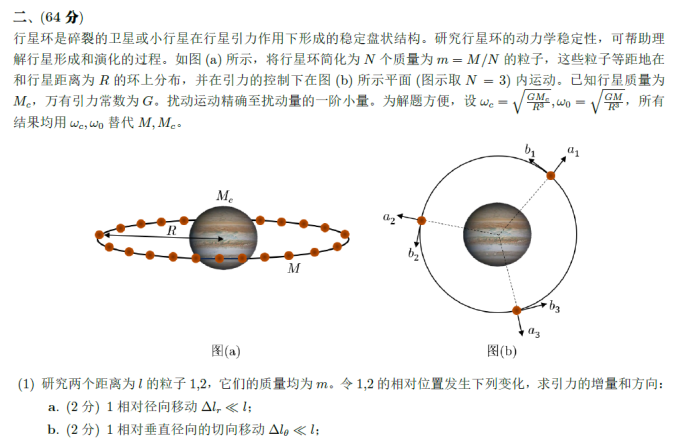

2024决赛刷题营试题:行星环动力学问题
第三题
第三题聚焦于光学干涉仪的矩阵表示和干涉原理,涉及马赫-曾德尔干涉仪(Mach-Zehnder Interferometer)、偏振态、以及复杂光学系统的相位差分析等内容。这类问题考查了学生对光学系统中光波行为的理解和矩阵描述的掌握,兼顾了理论和应用。问题背景光学干涉是经典光学中的核心内容,马赫-曾德尔干涉仪特别适用于分析光的相干性和相位差。
这类仪器在测量折射率变化、精密干涉测量等领域应用广泛。基于马赫-曾德尔干涉仪设计的题目可以让学生体会光波相干叠加和相位控制的原理。
第(6)(7)问题将马赫-曾德尔干涉仪与四象限干涉仪结合,考查了学生对光学仪器功能的理解。矩阵光学提供了简便的方法来描述光学器件对光的影响。在此题中,分束器、全反镜、偏振片、波片等元件都可以用矩阵表示,这种处理方法广泛用于光学和量子信息科学的研究中,当前物理竞赛环境基本已经把矩阵光学作为教学内容之一,例如机构秋季热光近代专题课讲义(光学进阶1、光学进阶4讲义)。

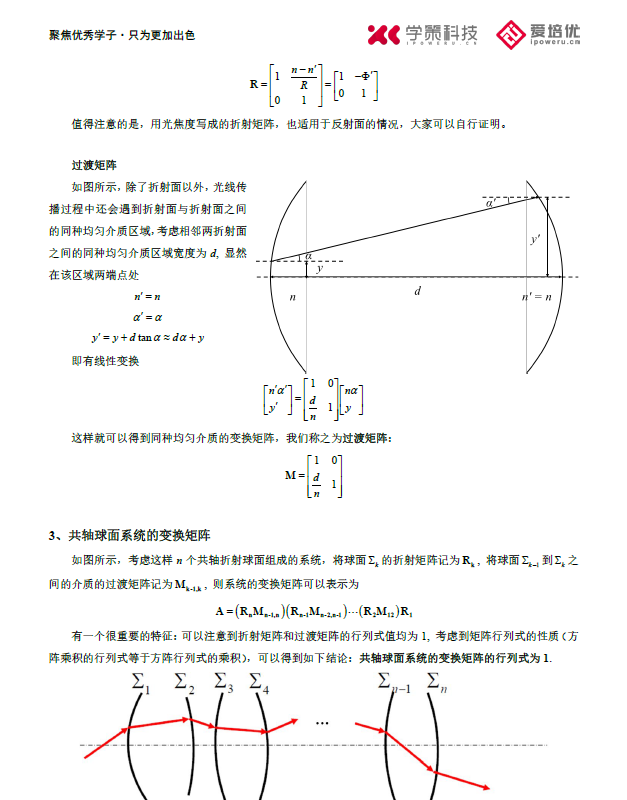


偏振的矩阵表示我们了解到的得分数据显示,本题得分的方差较大,这意味着本题有较大的区分度,这也是历届决赛光学题目的一个特点,在考场上看到光学大长题不敢动笔,这一幕同样出现在39决题目5的双折射问题中。
这类题目也尤其适合作为决赛题目以区分不同层次的学生。从教学实践的层面看,学生对于光学普物内容掌握普遍停留在基础层面,一方面光学进阶的内容相比于其它模块学习成本更高,而仅针对复赛,学习的收益性价比有限,同时市面上光学相关的优质模拟题目也相对稀缺,机构教研团队接下来将聚焦于这个问题,一方面继续提升光学进阶课程的讲义和选题质量,另一方面也更加侧重光学优质试题的研发。
第四题
第四题是一个两轮平衡车模型的力学分析问题,涉及经典力学中的多项知识,包括转动、稳定性分析、刚体动力学、小振动等。值得注意的是,本题满分为70分,是本试卷分值最高的题目。
但从我们拿到的得分数据来看,本题得分的情况并不理想,有多位理论160~190的学生,该题仅拿到<18的分数,甚至有数十位同学拿到个位数分数!!
平时练习被我们嫌弃的刚体问题(太无聊、没有趣味等),在考场上却摇身一变,成为了一道区分金牌还是集训队的题目。
题目简评
(1)问是基础性问题,要求计算平衡车在倾斜角度下匀速圆周运动的轨迹半径以及地面正压力的大小。此小问主要考查学生对离心力、正压力和角动量守恒的理解,是基础力学分析能力的直接考查。值得注意的是:该小问对于离心力矩不作用在质心,机构在近年的力学联考、刷题营、金牌联盟试卷三、力学拔高班等均对学生进行了反复的强调。
(2)问涉及平衡车直线加速过程中的扭矩和质心加速度。本小问复刻了38复赛第7题的问题,部分同学考前没有认真翻看官方竞委会出具的订正版答案,而沿用了初版错误的答案,导致在分析细杆时忽视了反向的扭矩,这样就几乎拿不到什么分数。正如同41复赛第五题考到了真题,给我们的启发是,在备考过程中,真题是非常重要的参考资料,同时务必要拿到订正版的题目与答案。
(3)问分析小振动,这是物理竞赛中的经典考点,要求学生计算一个动态系统的振动频率,并探索在不同系统参数下的频率变化规律。众所周知,机构刷题营一向重视刚体综合以及微振动问题,我们也一直认为刚体是决赛题目中看似容易拿分,但实则区分度非常高的一类题目。我们从已有的数据(查分前)随机的选出来理论总分在140~190之间的10位学生。
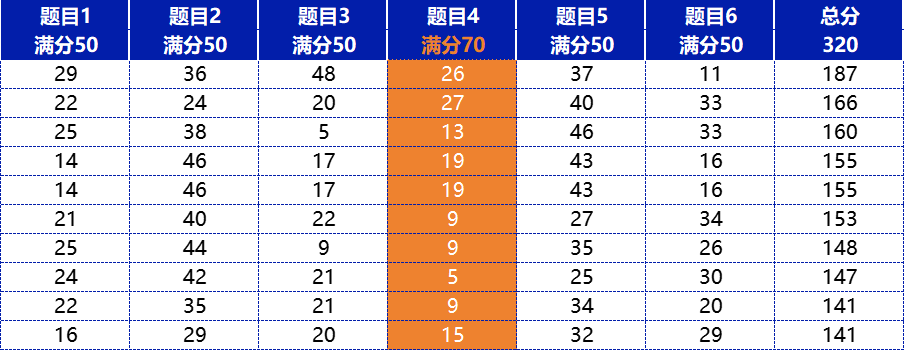
看了如上的分数条,不少教练可能会有疑惑:为什么有些同学“精通四大,熟悉固体物理、天体物理,拳打QED”,但是刚体题目只能拿到个位数的分数?有几点原因:
1,做题顺序问题,通过我们对学生的调研,先是受到第一题表述问题的影响,再接着2和3具有一定的阅读和计算量,等做到第4题时,看到70分大长题,大部分学生选择了先行跳过,而等到最后来解决这道题目的时候,很多同学都会遇到考试时间不够、自身精力不足的情况;
2,刚体题目不太依赖你见过了多少道类似题,而拼的是计算的熟练度与准确度,即使阅读了更多的物理专业的书籍,也并不能增加你做出来刚体题目的概率。换句话说,博闻强识的天赋型选手也不一定能在刚体部分表现得更加出色,反而是踏实沉稳、基本功扎实的同学,更容易拿到高分。
第五题
第五题聚焦于球对称恒星模型的结构和稳定性,这是一个典型的天体物理和流体力学问题,涉及引力、流体静力平衡、引力势能和热力学等内容。这类问题通过简化恒星内部结构的物理模型,考查学生对复杂系统的理解、建立微分方程求解方法的掌握,以及恒星结构稳定性和能量分布的综合分析能力。
问题溯源
该题的设置可能参考了《恒星结构与演化》(Stellar Structure and Evolution),这种恒星模型分析方法还可以在一些经典天体物理学教材如《Introduction to Modern Astrophysics》中找到类似例题,对于国内的教材,可以参考中科大出版的《天体物理概论 向守平》。关于球对称恒星的模型在今年机构的复赛、决赛营里均有所涉猎,如图:


2024机构复赛营

2024机构决赛营(1)至(4)考查球对称情况热力学建模,讨论不解体条件,其中光子气体的部分是同学们非常熟悉的内容;(5)至(7)问考虑了辐射效应,这是容易丢分的部分。辐射效应对恒星温度分布的影响涉及光压、辐射平衡和不透明度等概念,需要一定的物理模型化和抽象分析能力。
实际上该小问考查的背景是爱丁顿极限(Eddington Limit),又叫爱丁顿光度极限,是指恒星、黑洞或其他天体的辐射压力与其引力的平衡点。概念最早由英国天文学家阿瑟·爱丁顿于1926年提出,用于描述恒星的最大光度。
当一个天体的辐射能量流密度(光度)达到某一极限时,辐射压力将与引力产生平衡,这时天体不再能进一步增加亮度,否则其辐射将导致物质被“吹散”,无法保持结构。如果先前对这块内容已经有所了解,则可能拿到较高的分数,从第四题展示的分数条我们可以看出,大部分学生这道题可以拿到40+的分数。
第六题
第六题涉及量子力学中的不确定性原理和真空电磁相互作用力,这是一个结合了量子力学和电磁学的综合问题,题目不仅考查了学生对量子力学基础知识(如不确定性关系和基态能量)和电磁相互作用力的理解,还要求学生能够将这些概念应用到理想导体之间的电磁力计算中。
题目来源
这道题关于零点能量和卡西米尔效应的讨论参考了量子电动力学(QED)和量子场论中的经典问题,而本题目的图片和部分推导则是直接搬运自《QUANTUM FIELD THERORY and the STANDARD MODEL》Matthew D. Schwartz。
 参考书籍
参考书籍 多种正规化方式
多种正规化方式
不依赖函数选取的正规化
题目点评
不确定性原理是量子力学的核心概念之一,在复赛中的第四题和第七题都有相关内容的考查。在这道题目中,基于不确定性原理提出的“基态能量不可能为零”这一概念,启发学生理解量子场理论中的能量起源问题,特别是电磁场中的真空能量。真空不仅为空间中的空白区域,还包含着能量和场波动,这些波动即使在绝对零度下也存在。题目探讨了真空中的电磁场和导体之间的相互作用力,尤其是电磁零点能量如何影响物体之间的相互作用。
即所谓的卡西米尔效应(Casimir effect),对应的卡西米尔力源于虚粒子的涌现和在有限空间内的量子场波动。
(1)至(3),甚至第(4)小问题目中给的引导是足够的,即使先前没有学过QED,没有刷到过相关的题目,前四问也能拿下(前四问一共28分,从学生得分也能证明这个结论),而第(5)问将问题进一步复杂化,引入高频电磁波模式的贡献和导体表面电磁力的计算,要求学生处理更复杂的物理情境,考虑多种影响因素。这部分内容涉及量子场论中的高阶效应和数学技巧,如欧拉-麦克劳林公式和积分技巧,对数学的要求较高。
重整化是高能物理和凝聚态理论中非常重要的物理思想。在QED中,计算散射振幅的微扰展开时涉及到的圈图积分会出现发散现象,也就是积分无法收敛。
通过引入和本题类似的动量截断,再通过质量和电荷重整化将这一截断吸收进拉格朗日量的裸质量和裸电荷,这样的重整化操作即可以消除QED中所有圈图的发散;在凝聚态理论中,重整化群通过研究系统耦合参数随长度尺度的变化,发现各种临界现象存在普适性,通过重整化群的不动点思想可以计算出系统临界点附近的临界指数等等。本题讨论了重整化思想中的正规化操作,即通过引入截断或核来处理无穷发散问题。
本题(4)使用的正规化方式为heat kernel,而(5)则是不依赖函数具体形式的正规化,实际上正是[Casimir, 1948]所采用的方式,时隔76年出现到了CPhO试卷上,如果先前没有任何经验的学生,想在考场上严格的证明出(5)是非常有挑战的,实际上从我们拿到的数据来看,几乎没有学生拿到35+的分数,这与复赛第7题的后面几问情况相同。
猜测出题人是一位高能领域的老师,他出此题是希望在高等数学可以处理的框架下,帮助学生对高能物理和凝聚态理论中常见的重整化思想有更深刻的理解。