常见、但看不懂的图表（没人教而你要会的学术基础知识）

然而，有些图表虽然常见，但真正要深入分析却让不少同学感到头疼。比如，箱线图、残差图、玫瑰图……今天，老师就为大家详细解读那些常见却又不知如何下手分析的图表，让你轻松掌握图表分析技巧，提升学术能力。

01、箱线图：数据分布的“密码箱”

箱线图（Box Plot）反应数据的分布特征。

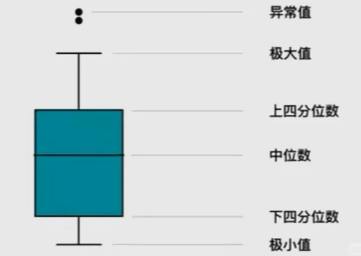
箱线图包含了6个关键特征值：

1、上限：除异常值外的最大值；

2、上四分位数：样本值从小到大排列，处于序列数75%位置的样本值；

3、中位数：序列数50%位置的样本值；

4、下四分位数：序列数25%位置的样本值；

5、下限和异常值：除异常值外的最小值；

6、异常值：异常值的判定通常基于一定的统计学规则，比如1.5倍四分位距（IQR=上四分位数-下四分位数）法则，超出上限+1.5*IQR或低于下限-1.5*IQR的值被视为异常值。

当我们拿到一个箱线图时，首先可以观察箱子的整体位置，它能大致反映数据的集中趋势。如果箱子位于较高的数值区域，说明数据整体偏大；反之，则偏小。其次，箱子的长度（即上四分位数与下四分位数的差值）代表了数据的中间50%的分散程度，长度越长，数据的离散程度越大。

例如，在比较不同区域的销量时，通过箱线图可以清晰地看到各区域的中位数差异，以及销量的分散情况。此外，异常值的存在也值得关注，它们可能是特殊情况的体现，比如某个产品因特殊事件导致销量过低或过高。02

残差图：回归模型的“质检员”

残差图（Residual Plot）在回归分析中起着至关重要的作用，是评估回归模型合理性的关键工具。残差是利用自变量x估计的回归方程去预测因变量y时产生的误差，也就是实际值与模型构建的理论值的差值。残差有以下几个重要的假定特性：均值为0，方差相等，相互独立，服从正态分布。

在分析残差图时，如果回归模型合理，那么残差图呈现出的总体印象应该是所有散点都随机地无规律地落在一条以0为中心的水平带中间。

相反，如果残差图出现明显的规律，比如散点呈现出某种曲线形状或者明显的趋势，那就说明回归模型可能存在问题，需要进一步改进。例如，可能需要添加更高次项的自变量，或者对数据进行变换等。

03、热力图：数据密度的可视化表达

热力图（Heatmap）通过颜色的深浅来表示数据的密度或数值大小，常用于展示二维数据的分布情况。

在分析热力图时，颜色越深的区域表示数据的密度或数值越大，颜色越浅则表示越小。例如，在分析校园内不同区域的人流量分布时，以热力图的形式展示各个区域在不同时间段的人流量情况，颜色最深的区域即为人员最为密集的地方，这对于校园规划、资源配置等方面有重要参考价值。

热力图还可以用于展示多个变量之间的相关性，如在基因表达数据分析中，通过热力图可以直观地看到不同基因在不同样本中的表达水平差异以及基因之间的相关性强弱，为进一步的生物学研究提供线索。

需要注意的是，在使用热力图时，要确保颜色的选择具有良好的区分度和可读性，避免颜色过于相近或刺眼，影响数据的解读。同时，对于颜色所代表的数值范围要进行明确的标注，以便读者准确理解数据的含义。

04、散点图：数据关联的“探测器”

散点图（Scatter Plot）是用于展示两个变量之间关系的常用图表。它通过将每个数据点的两个变量值分别作为横纵坐标绘制在平面上，从而呈现出数据的分布情况以及变量之间的潜在关联。

在分析散点图时，首先要观察数据点的整体分布趋势。如果数据点大致呈现出从左下角到右上角的上升趋势，说明两个变量之间可能存在正相关关系；反之，如果数据点呈现从左上角到右下角的下降趋势，则可能存在负相关关系。例如，在研究商品点击量与成交量的关系时，若散点图中商品点击量越多的成交量越高，那么就初步表明两者存在正相关。

同时，还要注意数据点的离散程度。如果数据点比较紧密地聚集在某条直线或曲线周围，说明变量之间的相关性较强；而如果数据点比较分散，可能意味着相关性较弱，或者存在其他因素影响了这种关系。此外，还可以通过观察是否存在异常的数据点（远离其他数据点的孤立点）来进一步分析数据的可靠性和潜在影响因素。对于存在明显相关性的散点图，我们还可以尝试拟合一条直线或曲线来更精确地描述变量之间的关系，并通过计算相关系数等统计量来量化这种相关性的强度。

05、多组差异散点图：差异基因的“全景展示”

多组差异散点图（Multi-Group Differential Scatter Plot）能够一次性展示多个比较组的差异基因情况。

在多组差异散点图中，通常以组间差异倍数的对数值log为纵坐标，以比较组的名称为横坐标。每个点代表一个样本量，点的颜色和大小可以用来表示基因的其他特征，如显著性水平等。

通过观察多组差异散点图，我们可以快速比较各个组之间的分布情况。此外，通过对不同组进行比较，还可以了解不同组之间的相似性和差异性，为进一步分类研究提供依据。

06、玫瑰图：周期性数据的“艺术展示”

南丁格尔玫瑰图（Nightingale Rose Chart）外观类似于圆形的柱状图，但将数据以扇形的形式分布在圆周上，每个扇形的角度和半径大小都与数据的数值相关。在分析玫瑰图时，要注意扇形的面积大小，面积越大，表示对应的数据值越大。

然而，玫瑰图也有其局限性。由于扇形的角度和半径同时用于表示数据，可能会在视觉上给人造成一定的误导，尤其是当数据差异较小时，难以准确比较各个扇形的大小。所以，在使用玫瑰图时，要确保数据的差异足够明显，以便读者能够清晰地解读图表所传达的信息。

07、雷达图：多维度数据的综合展示

雷达图（Radar Chart）是将多个变量的数值在一个图表中进行综合展示的有效方式，特别适合用于分析具有多个维度或属性的数据对象。

在雷达图中，每个变量对应一个坐标轴，从中心向外辐射，数据点连接起来形成一个多边形。通过观察多边形的形状和各边的长度，可以对不同数据对象在各个变量上的表现进行比较和分析。

比如，在评估学生综合素质时，可能会从学习成绩、社会实践、创新能力、团队协作、沟通能力等多个维度进行打分，将每个学生的各项得分绘制在雷达图上，就能清晰地看到该学生在各个方面的优势和不足。同时，也可以比较不同学生之间的雷达图，找出群体中的共性和个性特点。写在最后：在进行图表分析时，我们还需要注意一些常见的陷阱，以免得出错误的结论。

首先，阅读图表的标题（尤其时间）、坐标轴单位、标签、图例等元素；其次，在比较不同图表或同一图表中的不同元素时，要注意它们的单位和尺度是否一致，不一致的单位或尺度可能会导致数据的比较出现偏差，从而得出错误的结论。