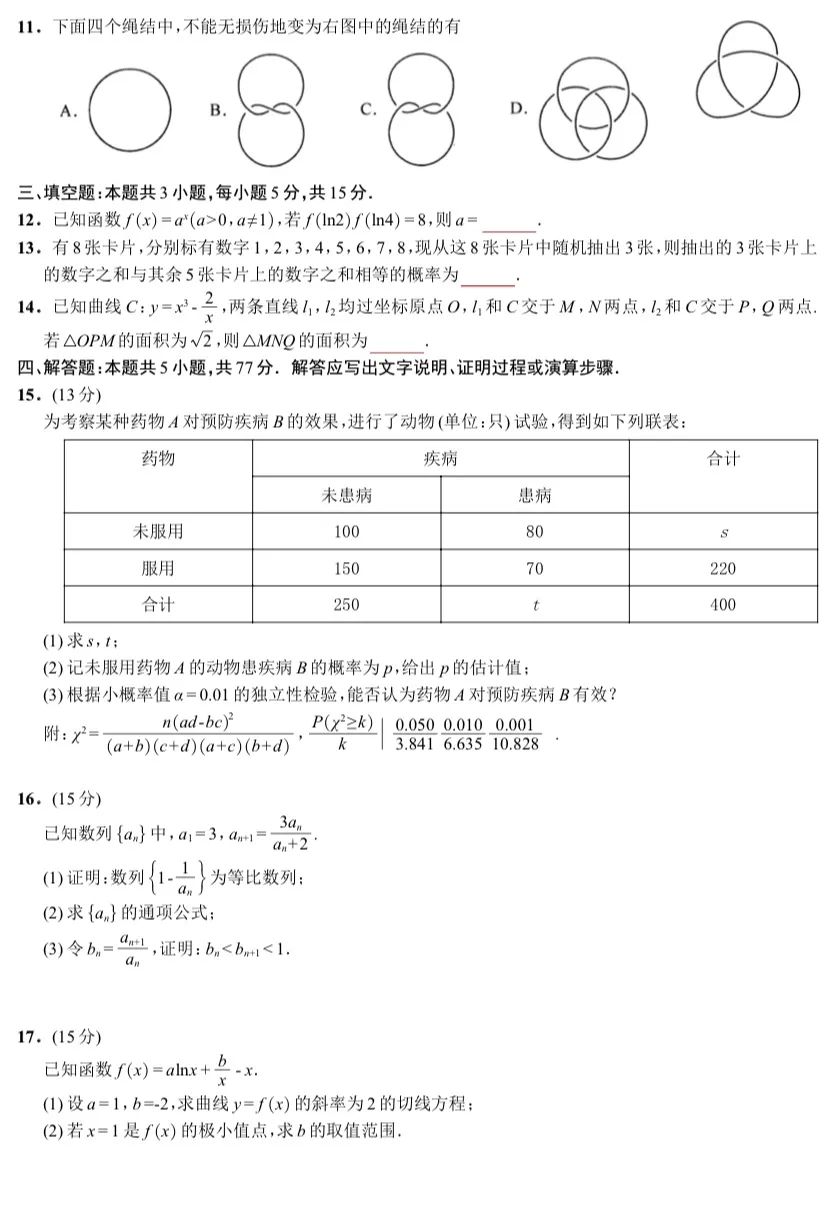
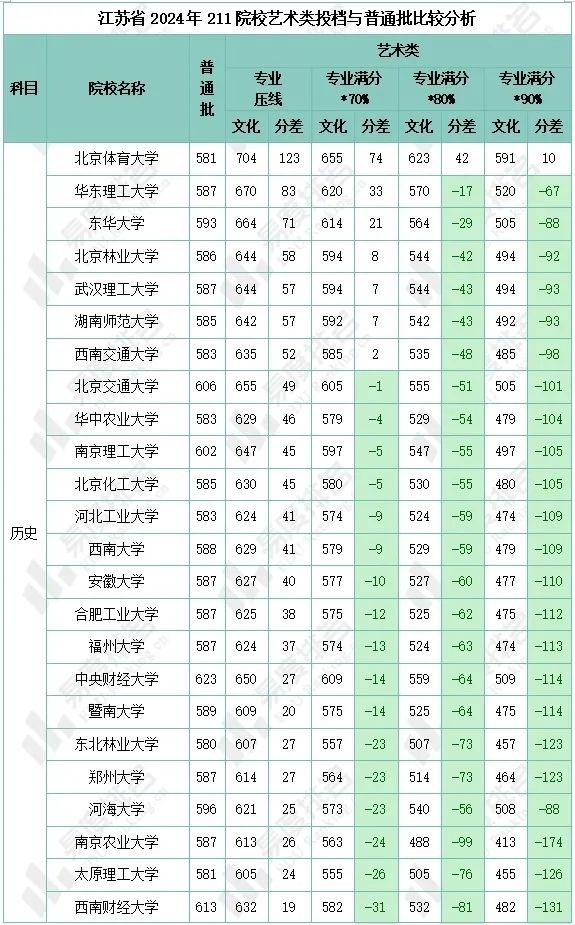
2025八省联考数学多选最后一题考了一个绳结问题 , 它的背景是纽结理论(Knot Theory) .
我们先来介绍什么是纽结?纽结是三维空间中的简单闭曲线 , 这说明纽结有着简单闭曲线的三个特征 , 分别是连通性 , 封闭性以及不自交性 , 特别地在一个平面内的圆圈也是一个纽结 , 我们称之为平凡纽结 . 为了进一步理解纽结 , 还需要给出一个概念 , 即有许多条不相交的简单闭曲线构成的空间图形称为链环 , 而组成链环的每一条简单闭曲线称为这个链环的一个分支 , 于是纽结就看看成只有一个分支的链环 . 因此在同一个平面内的若干个不相交的圆圈也组成一个链环 , 即平凡链环 .
事实上纽结和链环可以在空间中连续变形 , 但不允许剪断和粘合 , 如果一个纽结或链环在经过上述变换后能变成另一个纽结或链环 , 那么我们就称这两个纽结或这两个链环是等价的 , 我们将其定义为同痕 .
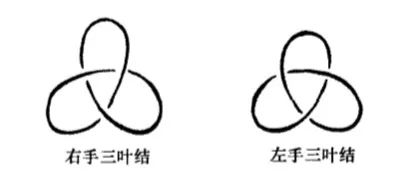
纽结中最基本的特点便是交叉点的个数 , 在数学上交叉点个数不超过 的只有平凡纽结 , 左手三叶结和右手三叶结 , 如上图所示 . 何为三叶结 , 就是旋转 的倍数角度后仍能和自身重合的纽结 . 接下来的任务就是如何区分左手三叶结和右手三叶结 , 故我们需要给出交叉点的定向的定义 , 如下图所示 .
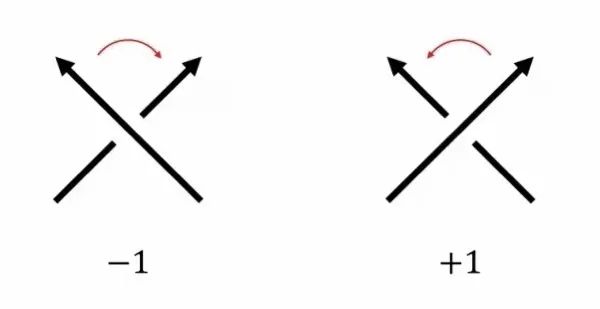
交叉点一共存在两种定向 , 如果从上方翻过去过箭头(上行线)绕交叉点顺时针旋转后与从下方钻过去的箭头(下行线)能重合 , 那么该交叉点记为 , 反之如果从上方翻过去过箭头(上行线)绕交叉点逆时针旋转后与从下方钻过去的箭头(下行线)能重合 , 那么该交叉点记为 , 因此用这个方法可以看到右手三叶结的三个交叉点的符号是 , 而左手三叶结的三个交叉点的符号是 , 进而可以说明左右手三叶结不是同痕的 , 当然要严格区分左右手三叶结还得借助 Jones 纽结多项式 .
Jones 多项式是纽结不变量 , 我们先来回顾三种 Reidemeister 变换 , 如下图所示 .
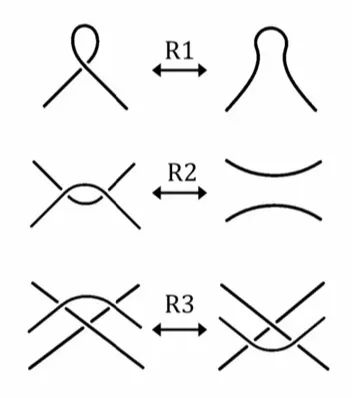
可以看到上面的三种 Reidemeister 变换中只有 变换会导致交叉点增加或减少 , 而 变换和 变换并不会改变交叉点的数量 , 也不会改变交叉点的总的定向 , 事实上关于 Jones 多项式的内容十分复杂 , 我们这里不加证明地给出结果 , 即如果两个纽结完全相同 ,当且仅当经过有限次Reidemeister变换后可以相互转换.
不论交叉点的定向是 还是 , 都可以通过 变换得到同一个结果 , 于是记下图中最右侧纽结的 Jones 多项式为 , 以及将交叉点的定向为 的纽结的 Jones 多项式记为 和交叉点的定向为 的纽结的 Jones 多项式记为 .
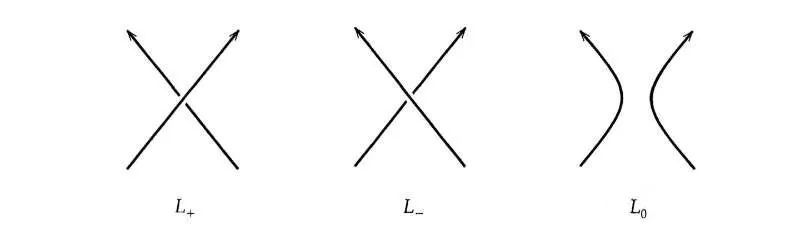
然后我们就可以给出计算公式 , 即
于是便得到 , 和 .
不妨设右手三叶结的 Jones 多项式为 和右手三叶结的 Jones 多项式为 , 我们再次给出三叶结的相关计算公式如下
于是得到 和 , 因此左手三叶结和右手三叶结不同痕 .
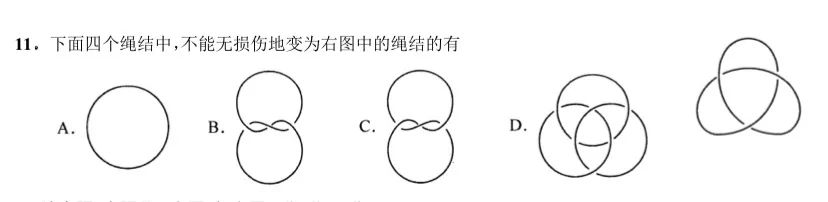
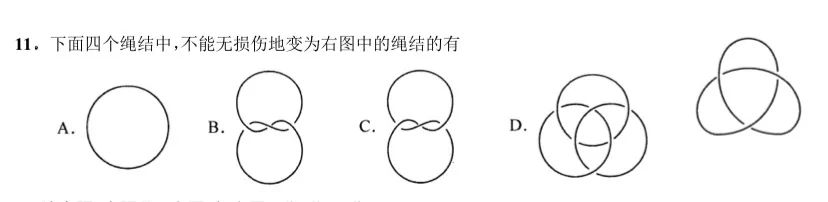
回到题目本身 , 由于题目所给的是左手三叶结 , 而选项中只有 C 选项是左手三叶结的另一种样貌(我们可以用交叉点的定向作出判断) , B 选项是右手三叶结的另一种样貌 , A 是平凡纽结 , D 是具有三个分支的链环 , 那么答案就一目了然了 .
最后附上2025年八省联考的全部试题 , 其他的题目全部都是高中范围内的普通题目 , 老师也懒得解答了 .