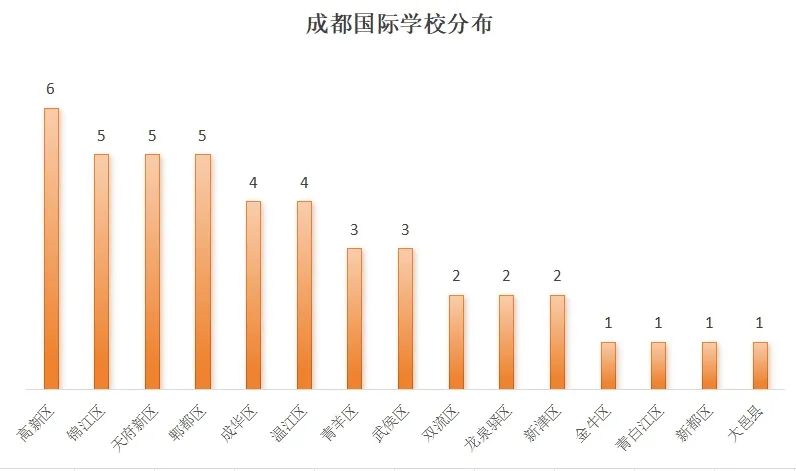
极限是我们学习微积分的重要基础,今天带大家学习一个简单的概念 — End behavior of polynomials。
首先,来学习一下词汇:
polynomial 多项式
the degree of polynomial多项式的次数
function函数
linear function 一次函数:is of the first degree
quadratic function 二次函数:has degree 2
cubic function 三次函数:has degree 3
constant 常数
coefficient 系数
infinite 无穷
even 偶数
odd 奇数
什么是polynomial function?
A polynomial function of degree n can be written in the form:
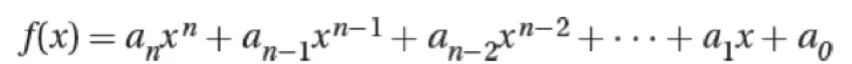 ,
,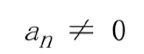
那么,什么是End behavior呢?我们可以理解为“终端趋势”,End behavior of polynomials即当x趋向于正/负无穷时(positively or negatively infinite),多项式(polynomial)所趋向的值。
先说结论:
Every polynomial whose degree is greater than or equal to 1 becomes infinite (positively or negatively) as x does, depending on the sign of the leading coefficient and the degree of the polynomial.
接下来我们结合图像来理解:
1.Quadratic function 二次函数

由图像可知,当a(leading coefficient)大于0时,
x → +∞,y → +∞
x → -∞,y → +∞
当a(leading coefficient)小于0时,
x → +∞,y → -∞
x → -∞,y → -∞
2.Cubic function 三次函数

当a(leading coefficient)大于0时,
x → +∞,y → +∞
x → -∞,y → -∞
当a(leading coefficient)小于0时,
x → +∞,y → -∞
x → -∞,y → +∞
3.Quartic function四次函数

当a(leading coefficient)大于0时,
x → +∞,y → +∞
x → -∞,y → +∞
当a(leading coefficient)小于0时,
x → +∞,y → -∞
x → -∞,y → -∞
以上我们不难看出(大家感兴趣可以画一下五次函数的图像),多项式次数(the degree of polynomial) 的奇偶性和首项系数(leading coefficient)的正负决定了函数图像的终端趋势,我们可以归类为:
1.If the degree n of a polynomial is even(偶),the arms of the graph(图像的两端)are either both up(a > 0)or down(a < 0);
2.If the degree n of a polynomial is odd(奇),one arm of the graph is up and the other is down:
when a > 0,the right arm of the graph is up
when a < 0,the right arm of the graph is down