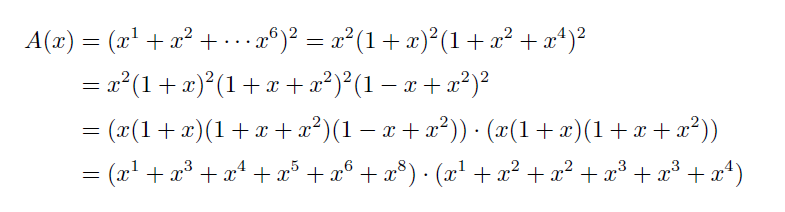违反直觉的骰子！

本月的每日一讲中 我们要深入探讨一个有名的问题：

Sicherman Dice 违反直觉的骰子

^{内容介绍✦}

我们将介绍所谓的Sicherman Dice，以及六面的Sicherman Dice 的唯一性证明。所谓的Sicherman Dice, 是George Sicherman 提出的，将两枚标准六面骰子上的数字全部替换为新的正整数，使得投掷之后概率分布都不变。

这最早是由Martin Gardner 在1978年提出的，当时的验证方法主要还是表格枚举。

现在我们可以利用generating function 的技术来证明这样的新骰子组合是唯一的，并且很快地找到这种骰子。

^{四面骰子✦}

我们假设有两枚标准四面体骰子，也就是两个正四面体四个面上分别都标有1，2，3，4，且投掷的时候每个数字出现的概率相同。

现在的任务是找到另外两枚四个面上的数都是正整数的正四面体骰子, 它们上面的数字都不是1，2，3，4，但是它们投掷的时候出现的概率分布是和标准4面骰子一样的。

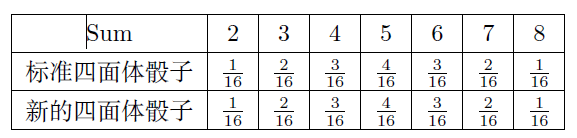
我们首先给出构造: (1，2，2，3) 和(1，3，3，5)，并通过表格验证这种新的四面体骰子满足条件。

这是很神奇的事情，如果在赌局当中荷官拿出的是这种骰子，你很难说服自己这两枚骰子和标准骰子是一样公平的。

下面我们利用generating function 来先解决概率分布，再解释这种构造的来源。

^{六面Sicherman Dice✦}

利用刚才对于OGF的因式分解技巧，我们可以很快得到六面骰子的Sicherman Dice，其中标准六面骰子就是标有1，2，3，4，5，6 的正方体。

这样，Sicherman Dice就是(1，3，4，5，6，8) 和(1，2，2，3，3，4)，两组比较神奇的数字。我们在第四个等号当中划分的依据实际上是要求六次多项式和常数项非零，读者可以自己尝试一下就知道除了标准六面骰子，只有这一组划分是合法的。

^{八面Sicherman Dice✦}

如果仿照刚才的做法，八面体骰子会稍微复杂一些， 因为我们需要讲16次多项式划分为没有常数项的八次多项式。如果大家有兴趣可以思考一下这样的划分有几个，并在后台提交答案。在这里我们只给出一个：(1，3，3，5，5，7，7，9) 和(1，2，2，3，5，6，6，7)。