MAT考试中的策略问题如何作答！

MAT 是由剑桥大学招生考试服务中心与牛津大学合作推出的数学系入学考试，其全称为 The Mathematics Admissions Test。该考试主要针对牛津大学数学、计算机科学相关专业，以及伦敦帝国理工学院和华威大学数学相关专业的申请人。

MAT 考试一般于每年的 9 月开始报名、10 月中旬报名截止、11 月初考试。其考试成绩不会被直接公布或标记是否“通过”，而是直接发往考生注册考试时填写的申请院校，根据测试中的相关信息来确定是否入围。

可以说，MAT 成绩的高低是牛津大学筛选面试学生和确认最终录取名单的重要衡量标准。

策略性问题虽然在数学竞赛中比较冷门，但这类问题凭借在经济金融学领域的重要地位，在诸多名校的自主招生考试中十分常见。

今天，让我们一起跟随机构张凡老师一起深度解析 MAT 考试中的策略性问题该如何思考作答！

突破牛剑 G5 防线第一步 火眼金睛辨“真身”

虽然策略性问题在自主招生考试中扮演着十分重要的角色，但有趣的是，这类问题并不总是直接了当地表明自己是策略类问题，而是悄悄把自己伪装好等待你的发现。

MAT策略性问题—真题讲解 1

下面，我们来通过几道真题详细为大家展开讲解，比如 2022 年 MAT 中的第 5 题压轴题?

本题除了最后一问之外，其他小问都是构造问题。类似于小学竞赛中找到有一种情况满足题意。

而最后一问就非常有趣了，题意大致可以整理如下?

Q：有六扇门一字排列，门后有六个不同的礼物。Alice 每次可以选择一扇门打开，并看到某一件礼物。每看到一件礼物之后，主持人都会把 Alice 看到的礼物和旁边一扇门后的礼物交换位置。最终凡是被 Alice 看见的礼物都会送给 Alice。如果 Alice 能选择开门的次数不受限制。那么 Alice 能否确保拿走所有礼物？

答案是：不能。

如果只是将本题当作一道数论或者组合的常规题目，那无疑会让你头疼不已，因为这个问题其实是一道策略博弈问题。而且游戏的参与者除了 Alice 之外，还有主持人。事实上，Alice 无法确保拿到 3、4 号门之一后面的礼物。

解题思路：

我们把主持人也当作游戏的参与者，那么如果 Alice 选择在 1、2 中开门，主持人只需交换 1、2 门后礼物的位置，选择 5、6 同理。如果在 3、4 号门中，Alice 先选择了 3 号门，此时我们可以假定主持人能够看穿 Alice 后面的所有选择。

如果忽略掉 Alice 选 1、2、5、6的情形（若选了按上述操作执行即可），若下一次 Alice 选择中间两扇门时将会选 3 号门，那本次 4 号门位置不变；若下一次 Alice 选择中间两扇门中的 4 号门，那本此把 3、4 号门后的礼物调换。后面情况以此类推，主持人可以保证 Alice 永远拿不到 4 号门后的礼物。

因此，Alice 永远无法确保拿到六扇门后面的所有礼物。

本题的难点在于辨认出这是一道必胜策略问题而非数论组合问题。一旦发现它的本来面目，那么解决这个问题就变得非常简单。

突破牛剑 G5 防线第二步 敏锐准确看“本质”

但有时，我们要发现策略问题其实是一道数论组合问题，比如清华大学 10 年的自主招生考察了这样一道题目?

Q：比赛开始后，12 个人每人的头上将会带一顶帽子。这些帽子分别是红、黄、紫、蓝四种颜色之一。每个人能看到别人头上帽子的颜色，而看不到自己头上帽子的颜色。比赛开始前，12 个人可以商量出一种策略，以保证比赛开始后，12 个人可以依次说出自己头上帽子的颜色，并尽量让每个人都说对的概率最大。请问这个最大值是多少？

本题看似是一个策略问题，但其实是一道数论问题。

解题思路：

由于第一个人报颜色的时候没有任何其他信息，所以他说对的概率就是 1/4，因此可以推断出全部说对的概率不会超过 1/4。

我们可以把 4 种颜色看作是摸 4 的四个余数 0、1、2、3。红对应 0，黄对应 1，紫对应 2，蓝对应 3。

让第一个人报出其他十一个人帽子上数字加和除以 4 的余数。除了第一个人之外，所有人都能看到第一个人帽子的颜色。于是剩余的 11 个人都能知道 12 个人帽子上数字的总和除以 4 的余数，再加上他们本来就能看到的除了自己之外其他人帽子上数字总和除以 4 所得的余数。因此，就可以推出自己帽子上的数字，进而知道自己帽子的颜色。

所以，本题其实是一道由数论知识寻找最优策略的问题，该题的结果是 1/4。

北上家长都在“卷”的数学竞赛 究竟为哪般？

许多高校的入校考试都热衷于考察策略类的问题。不仅因为策略类问题是能够开发智力的逻辑游戏，更因为博弈理论能解释一些有趣社会现象背后的原理，也是经济学的重要基础之一。

比如博弈论就可以解释北京上海的数学竞赛为什么这么火。要搞清楚这个问题，首先就要搞清楚为什么这么多家长会选择报奥数班。

从经验上看，别的家长是否报名竞赛班是否会对你的决策产生影响，这可以看作是一个多人博弈的问题。但是为了简化起见，我们假设两个家长 A、B 作为博弈的参与者，人大附中要选择这两个家长之一的孩子入学。

我们假设两个孩子的天分是完全一样的。如果一方报班，另一方不报班，那么报班的必然被录取。如果双方同时报班，或同时不报班，则各有百分之五十的概率被录取。

由此，我们可以写出这个博弈的效应矩阵：如果 A 报班，B 不报班，那么 A 孩子被录取收获效用 1，B 收获效用 0。如果 B 报 A 不报，那么 B 收获效用 1，A 收获效用 0。

如果 A、B 都不报班，那么各有百分之五十的概率被录取，各收获效用 0.5。如果 A、B 都报班，由于报奥赛班要花很多的钱和时间，所以各收获效用变少假设为 0.1。

以上思路可整理为下图所示：（图中每个方格里两个数字，左面是 A 获得的效用，右面是 B 获得的效用）

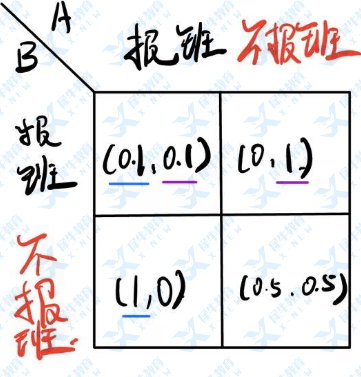
在 A 选择报班的情况下，若 B 选择报班，则收获 0.1，选不报班，则收获 0，于是我们在第一列当中选择右侧的 0.1 下面画紫线。在 A 选择不报班的情况下，B 选择报班，则收获 1，选择不报班收获 0.5。因为 1 更大，所以我们在第二列方格中右侧的 1 下面画紫线。

同样的，我们假设 B 选择报班或不报班，观察 A 获得的效用，可以画出 A 对应的选择。

显然，只有当某一方格中两个数字下面都画了线，A、B 才没有改变自身策略的动机。观察矩阵图不难发现，只有 A、B 都选择报班，这个博弈才处于稳定状态。其它情形都至少有一方会主动改变自身策略。

因此，哪怕如果 A、B 选择都不报班能获得比都报班更高的效用（都不报班双方都获得 0.5，都不报班双方都获得 0.1），也就是说 A、B 都不报班，双方都能过得更好，但 A 和 B 两位家长也会毅然决然地选择内卷，这就是北京上海奥数班为什么这么火的原因。