数学建模竞赛发展到今天已经有几十年的历史,所诞生出的模型也百花齐放,各有各的特点,短时间内掌握全部模型是不可能的,但我们可以学习经典模型,吃透这些经典模型,其它方法也能触类旁通。今天我们介绍美赛中常见的几类问题(评价、决策、预测、聚类和最短路)求解方法。
01层次分析法(AHP)——评价/决策问题
层次分析法是将定性问题定量化处理的一种有效手段,因此它可以广泛用于评价问题和决策问题。面临各种各样的方案,要进行比较、判断、评价、最后作出决策,例如去某地旅游要考虑景色、费用、居住、饮食和旅途等费用,不同地区在这些方面各有特点,如果只是凭借经验处理这些问题,主观性较强,不能使人信服。
第一步:建立层次结构模型
一般分为三层,最上面为目标层,最下面为方案层,中间是准则层或指标层。
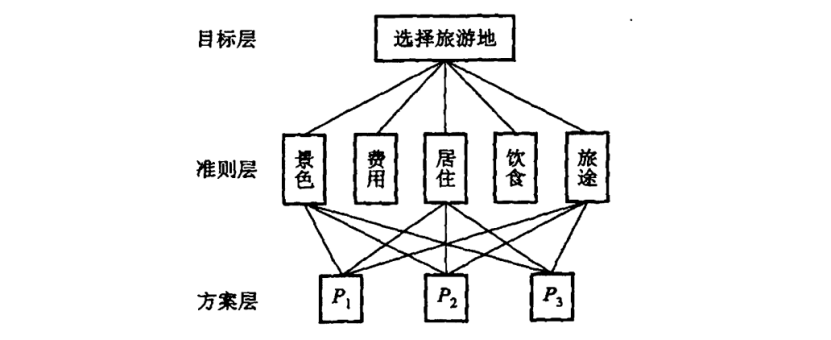
在层次划分及因素选取时,我们要注意三点:
1. 上层对下层有支配作用;
2. 同一层因素不存在支配关系(相互独立);
3. 每层因素一般不要超过9个。
第二步:构造成对比较阵
面对的决策问题:要比较n个因素对目标的影响。我们要确定它们在目标层中所占的比重(权重),可以用两两比较的方法将各因素的重要性量化(两个东西进行比较,最能比较出它们的优劣及优劣程度)。如何确定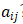 ?
?

最终成对比较矩阵A=(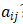 ),如下图示例:
),如下图示例:

第三步:一致性检验
我们发现,在给出成对比较矩阵的时候存在一定主观性,因此需要通过一致性检验判断成对比较矩阵的合理性。
1、计算一致性指标CI用来衡量成对比较矩阵的不一致程度。
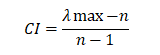
2、查找相应的平均随机一致性指标RI

3、计算一致性比例CR
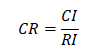
当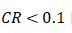 时,认为矩阵A的不一致性是可以接受的,反之,应该修改成对比较矩阵。
时,认为矩阵A的不一致性是可以接受的,反之,应该修改成对比较矩阵。
步骤四:计算权重向量
求矩阵A的最大特征值所对应的向量,并归一化,即可作为权向量。权向量的各个权重就是决策层对目标层的影响大小。把每一层对上一层的权重依次乘起来,即可得到最终的权向量,有大到小排列即可得到评价标准或者决策方案。
注意以下2点:
1、层次分析法只能从现有的方案中选择出较优的一个,并不能提供出一个新的或是更好的方案来;
2、建立层次结构及成对比较矩阵,主观因素起很大作用,这是一个无法克服的缺点,因此我们建议比赛时如果要用这种方法,可以在网上查找充足的资料,再由小组共同打分或者单独打分取平均值,以此规避主观性,此外,一致性检验必不可少。
02狄克斯特拉(Dijkstra)算法——最短路问题
最短路问题是图论应用的基本问题,很多实际问题,如线路的布设、运输安排、运输网络最小费用流等问题,都可通过建立最短路问题模型来求解。
Dijkstra算法采用的是一种贪心的策略,为了在计算机上描述图与网络,我们采用邻接矩阵表示法,其中邻接矩阵是表示顶点之间相邻关系的矩阵,记为
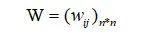
声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T。初始时,原点 s 的路径权重被赋为0(dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。即根据距离给W赋权:

初始时,集合T只有顶点s。然后从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,此时完成一个顶点。然后我们需要查看新加入的顶点是否可以到达其他顶点,并且查看通过该顶点到达其他点的路径长度是否比原点直接到达短?如果是,那么就替换这些顶点在dis中的值,然后又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
03k-近邻算法(KNN)——聚类问题
聚类问题常见于数据处理,聚类算法通过感知样本间的相似度,进行归类归纳,对新的输入进行输出预测,输出变量取有限个离散值。KNN是一种基于实例的监督学习算法,选择合适的参数k就可以进行应用。
k近邻法的特殊情况是k=1的情形,称为最近邻算法。
优点:精度高、对异常值不敏感、无数据输入假定;缺点:计算复杂度高、空间复杂高。
算法三要素:k值的选择、距离度量、分类决策规则。如果选择较小的值,分类结果会对近邻的实例点非常敏感,如果邻近的实例点恰巧是噪声,分类就会出错;如果选择较大的值,与输入实例较远的(不相似的点)也会对分类产生影响,使分类发生错误。关于如何选择合适的k,没有固定的计算方法,而是依赖经验。
距离的度量一般采用欧氏距离,优点在于计算量小,容易解释且足够准确。
分类决策规则采用"投票法" ,即选择这k个样本中出现最多的类别标记作为预测结果或者采用"平均法" ,即将k个样本的实值输出标记平均值作为预测结果;还可基于距离远近进行加权平均或加权投票,距离越近的样本权重越大
04灰色预测——预测模型
对于一些预测问题,如气象预报、地震预报、病虫害预报等可以用灰色预测模型解决。
灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
步骤一:生成数列
通过对原始数据的整理寻找数的规律,分为三类:
1. 累加生成:通过数列间各时刻数据的依个累加得到新的数据与数列。累加前数列为原始数列,累加后为生成数列。
2. 累减生成:前后两个数据之差,累加生成的逆运算。累减生成可将累加生成还原成非生成数列。
3. 映射生成:累加、累减以外的生成方式。
步骤二:建立模型
把原始数据加工成生成数,对残差(模型计算值与实际值之差)修订后,建立差分微分方程模型,基于关联度收敛分析。GM模型所得数据须经过逆生成还原后才能用。
以上就是美赛中常见的数学模型,大家可以注意到,有些模型涵盖了多个问题,比如层次分析法既可以解决决策问题,也可以解决评价问题,这启发我们竞赛时既要根据问题选择合适的模型,又要灵活运用模型做出合理的优化。希望同学们可以熟练掌握以上模型,并且在此基础上不断学习,一方面探索经典模型的优化方法,学会“旧瓶装新酒”,另一方面学习新的方法,不断扩充自己的知识体系。












