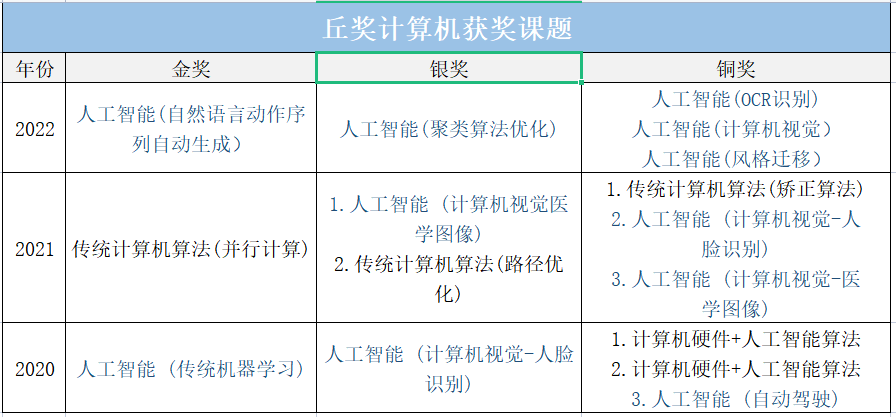
五月小讲堂
本月的每日一讲中
我们要深入探讨一个2022 AMC12中的一道问题:
2022 AMC12A P24
内容介绍✦
2022年的AMC12A 24考到了这样一个问题:

这个问题本身是非常容易看出答案的,虽然它位于24题,但是选项的给法非常巧妙,这也导致我们忽略了它背后的思考。
Solution 1:

但是这个问题还有一种思考,来源于MAA官方解答:

这就是非常著名的Parking Functions ,最早是由Henry O. Pollak提出的,在本月的问题中,我们简单介绍一下这个function的证明,以及一些后续的发展。
Theorem (Parking Function) 对于1,2,…n的直线排列车位,车辆![]() 事先想停入
事先想停入![]() 。但是如果已经被
。但是如果已经被![]() 占用,则它自动停入下一个无车的车位。我们将这个先验的排列
占用,则它自动停入下一个无车的车位。我们将这个先验的排列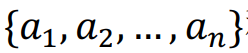 称为一个parking function,如果所有的车子都是可以停入车位的。这样的parking function 总共有
称为一个parking function,如果所有的车子都是可以停入车位的。这样的parking function 总共有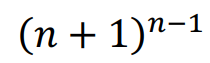 种。
种。
Proof: 我们增加一个车位n+1,并把这些车位排成一个圈,注意n+1现在认为也可以被用来停车。
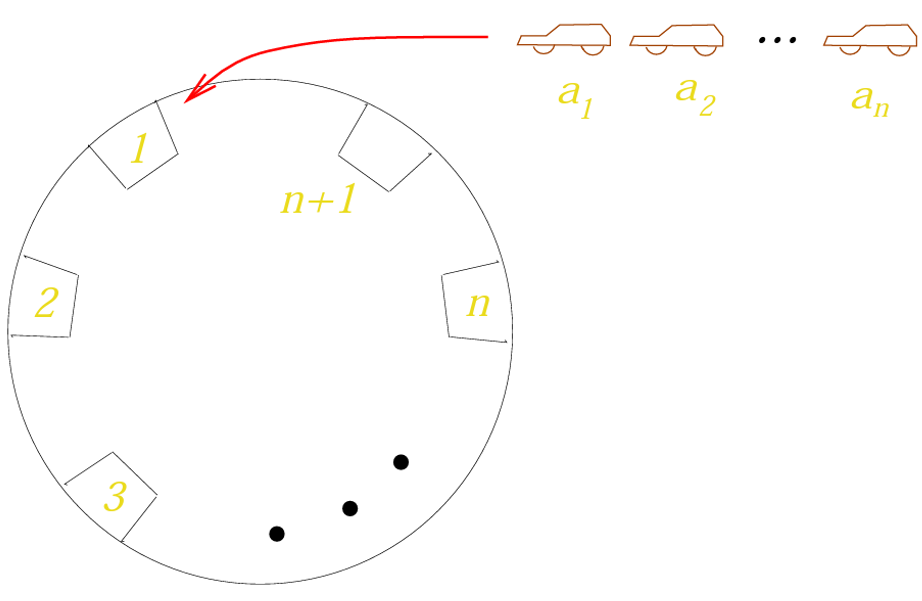
注意此时所有的车都可以停入,并且会空着一个位置。显然一个排列是个Parking Function,当且仅当它的空位是n+1。
注意,如果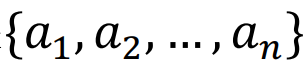 使得
使得![]() 停入了
停入了![]() ,则
,则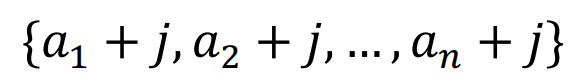 将使得
将使得![]() 停入了
停入了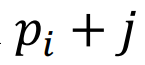 。这意味着对于
。这意味着对于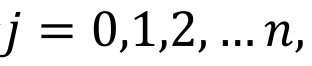 当中只有一个是Parking Function(空出了n+1的位置),故答案为
当中只有一个是Parking Function(空出了n+1的位置),故答案为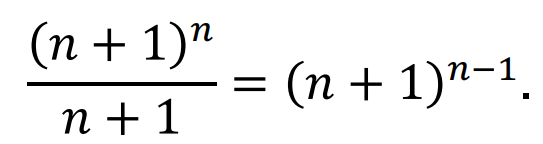 熟悉图论的同学此时一定会发现,这个问题的结果和
熟悉图论的同学此时一定会发现,这个问题的结果和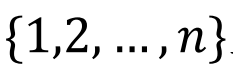 上的 Rooted Forest个数是一样的!这里 rooted forest 实际上是 rooted tree 的无交并,当然后者实际也就是在 tree 上指定一个 root,与之对应的概念是 free tree。 Theorem (Cayley) {1,2, … , ?}上的 Rooted Forest 有(? + 1)?-1种。 我们给出 ?=3 的例子:
上的 Rooted Forest个数是一样的!这里 rooted forest 实际上是 rooted tree 的无交并,当然后者实际也就是在 tree 上指定一个 root,与之对应的概念是 free tree。 Theorem (Cayley) {1,2, … , ?}上的 Rooted Forest 有(? + 1)?-1种。 我们给出 ?=3 的例子: 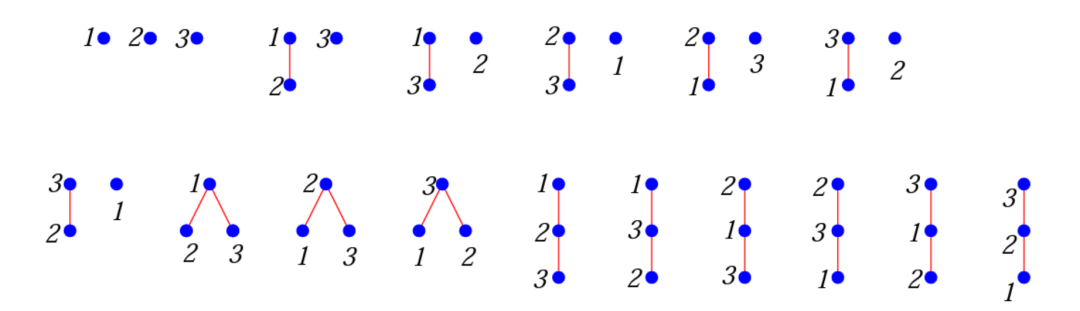 有兴趣的读者可以想想这个定理的证明,它属于 Sylvester。当然, Parking Functions的应用不止于此,它实际上还和无交分拆(Noncrossing partitions)有密切的关系,它是指
有兴趣的读者可以想想这个定理的证明,它属于 Sylvester。当然, Parking Functions的应用不止于此,它实际上还和无交分拆(Noncrossing partitions)有密切的关系,它是指
Definition Noncrossing Partition 是对于{1,2, … , ?}的一种分拆 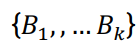 ,使得: 若 ? < ? < ? < ?, 且 ?, ? ∈
,使得: 若 ? < ? < ? < ?, 且 ?, ? ∈ ![]() , ?, ? ∈
, ?, ? ∈ ![]() 则 ? = ?.
则 ? = ?.
其中![]() 称为 block。 形象地来看:
称为 block。 形象地来看:
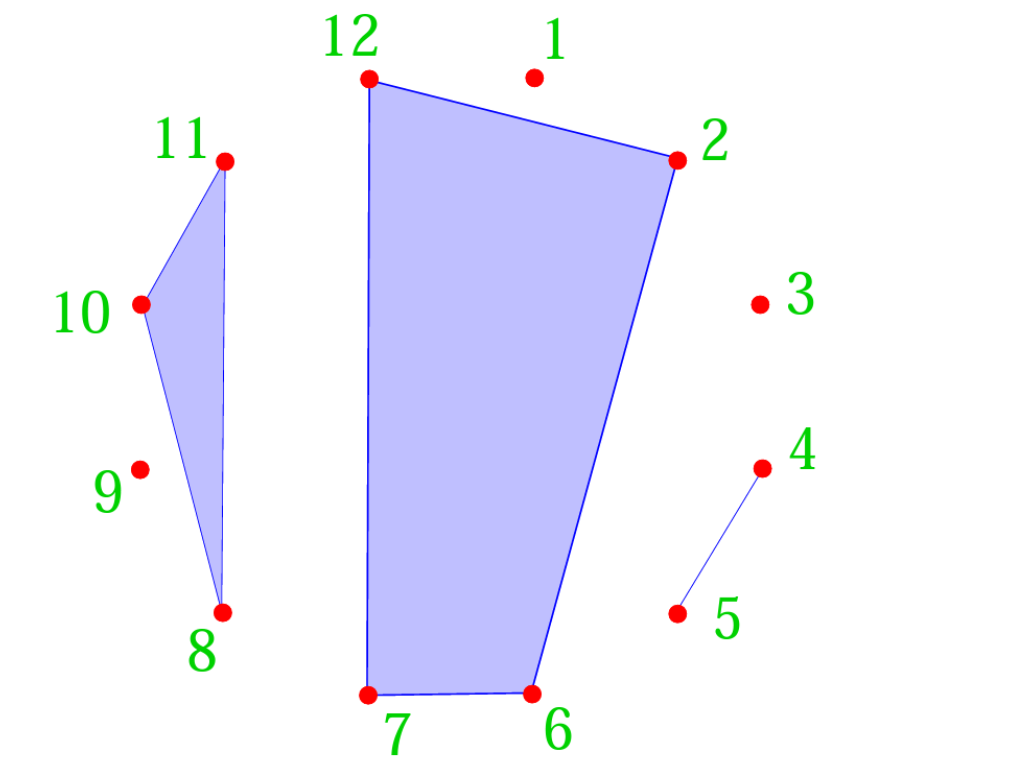
当然 Noncrossing Partition 应该是有 Catalan Number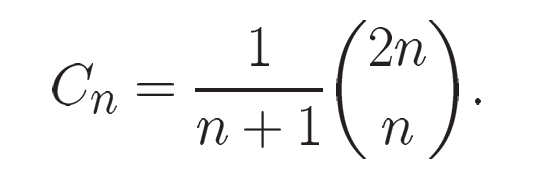 个的,这里我们不多对此结果作注释。
个的,这里我们不多对此结果作注释。
值得提的是所谓的 Parking Function 是和极大链一一对应的,换言之极大链恰好有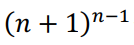 个。数列 m 是{1,2,…,n+1}的Noncrossing partition 的极大链(maximal chain),如果 m =
个。数列 m 是{1,2,…,n+1}的Noncrossing partition 的极大链(maximal chain),如果 m = 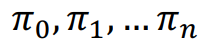
其中, ![]() 是一个{1,2,…,n+1}的 Noncrossing partition,且
是一个{1,2,…,n+1}的 Noncrossing partition,且![]() 是通过合并
是通过合并![]() 的 block得到的,例如:
的 block得到的,例如:
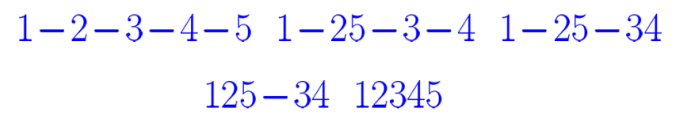
就是一种 maximal chain。有兴趣的读者可以想想这种一一对应本质上是什么?