MAT考试高频考点分析

MAT考试涉及到的知识点很多，绝大部分A-Level数学、进阶数学的知识都可能被涉及到。那在MAT考试之中，有没有那种出现频率特别高，必须要牢记的高频考点呢？   今天机构老师就来带大家一起看一看?

01用正弦函数表示的三角形面积公式

三角形的面积有多种表示方法，大部分同学对于最朴素的表达公式：底乘高除以2都非常熟悉。但是进入高中阶段之后，记住使用正弦函数和两边长度表达的三角形面积公式就非常重要。

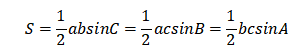
 例如2021年MAT考试的第一个选择题：

这个选择题通过带三角函数的面积公式就可以迅速秒掉。而如果专门求底边长度和高的话，计算起来会比较复杂，需要学生记住15度的三角函数，或者能熟练运用三角函数的二倍角公式。通过用正弦函数表示的三角形面积公式我们可以迅速得到：

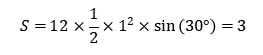
02直线的点斜式表达

MAT中经常需要求过定点斜率已知的直线方程，这时候设斜截式方程然后带入求解参数虽然也能得到结果，但是计算的复杂程度会明显提升。熟悉点斜式方程的写法，直接写出点斜式方程，可以减少自己的计算量，为后面更复杂的题目争取时间。对于过定点，斜率为k的直线，他的点斜式方程为：

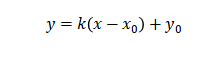
例如2021年MAT考试的第三个选择题：

通过斜截式，迅速写出在每个点的切线方程，求解起来就会方便很多。

03二项展开式及升级版

二项展开是A-Level数学的重要内容，在MAT考试中也经常涉及。而一些难度较高的题目中，还会涉及到二项展开的升级版本，三项展开、四项展开等等。如果没有学过升级版本的展开表达式，就只能自己现场二项展开成多项，然后继续展开，就会变得比较麻烦。

三项展开的公式为：

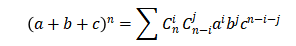
比如2022年MAT考试的第五个选择题：

直接使用三项展开公式，就可以把其中的常数项直接求出来：

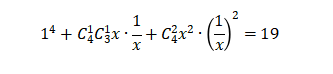
04三次函数绘图

MAT中经常考察三次方程的解的数量问题。三次方程的求根公式非常复杂，我们无法通过求根公式判断解的数量。这时候通过计算正确绘制三次函数图形，从而根据图形和x轴的交点数量，确定三次方程的解的数量就非常重要。绘制图形的时候，一定要通过计算确定函数的极值点位置，进而根据极值点的有无，以及在x轴的上方还是下方确定大致的图形长相。

例如2019年的选择题第一题：

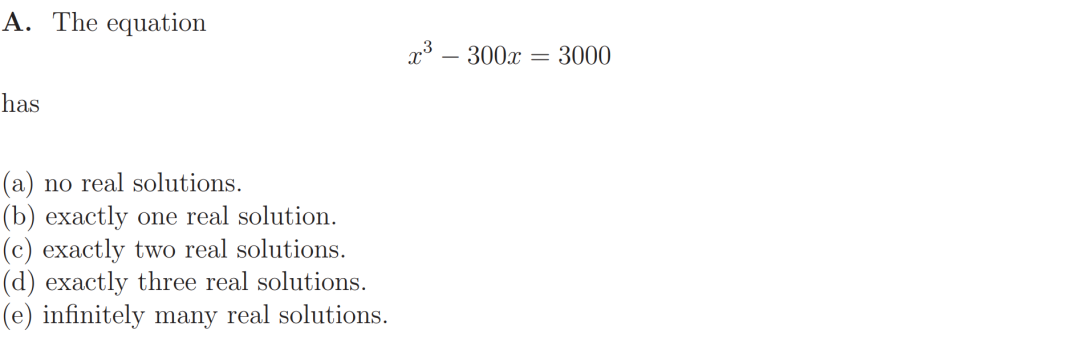
这个三次方程没有有理数解，无法通过试根等方法确定解的值。因此只能通过三次函数绘图法。记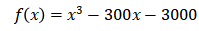，考察导函数：

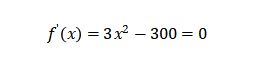
解得x=±10，对应两个极值点（10，-5000）和（-10,-1000）从而画出函数图像：

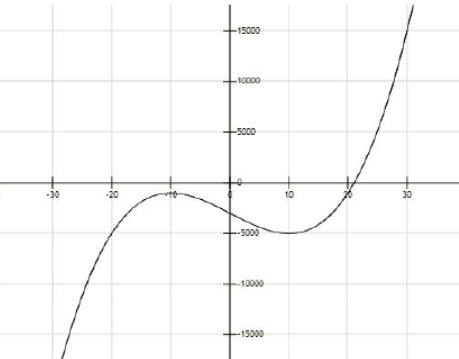
进而确定函数等于0只有一个解。

为了帮助有志于参加MAT并冲击高分的的同学备考，MathMaster教研团队研发了备考冲刺课程——针对MAT这些独特的考试题型，我们设计了MAT知识课程以及刷题课程。

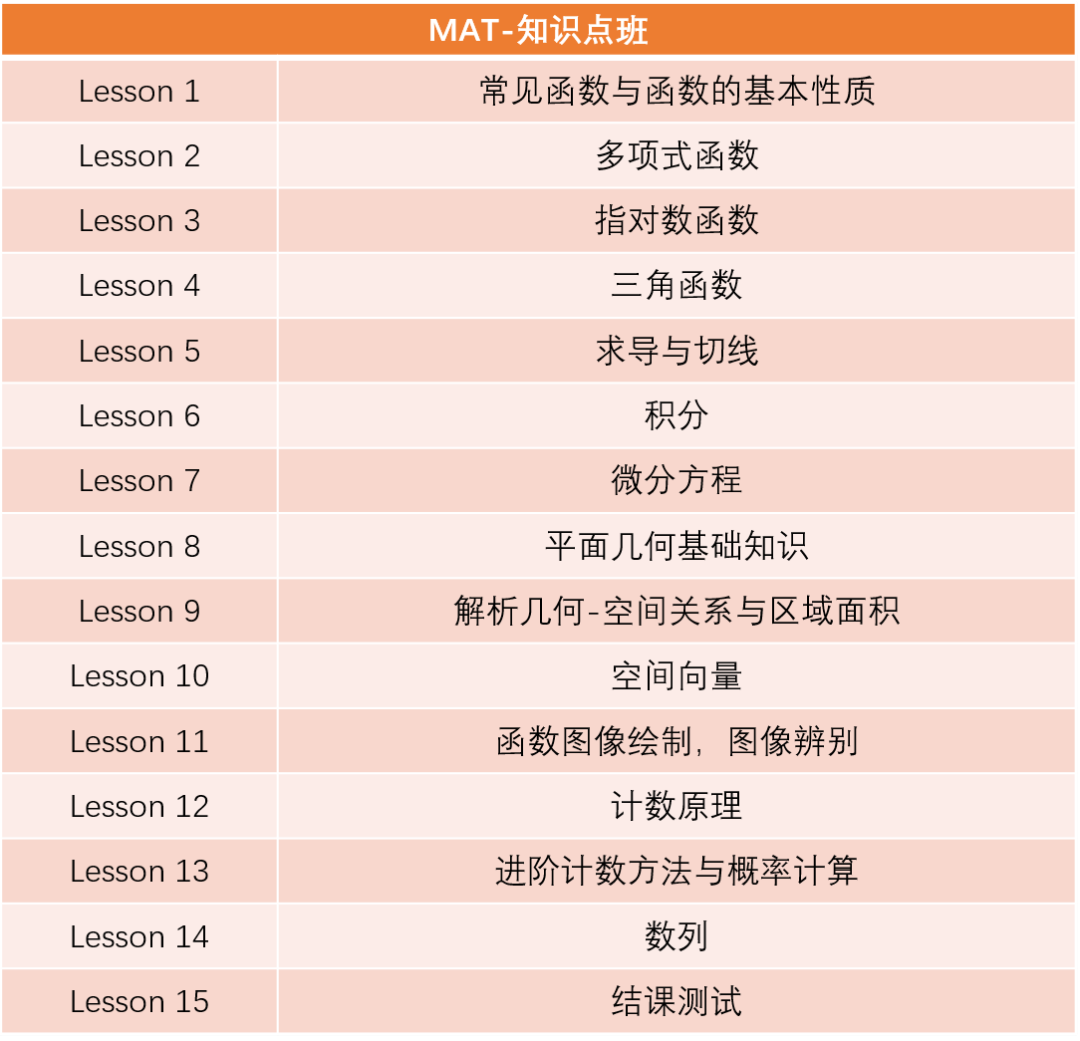
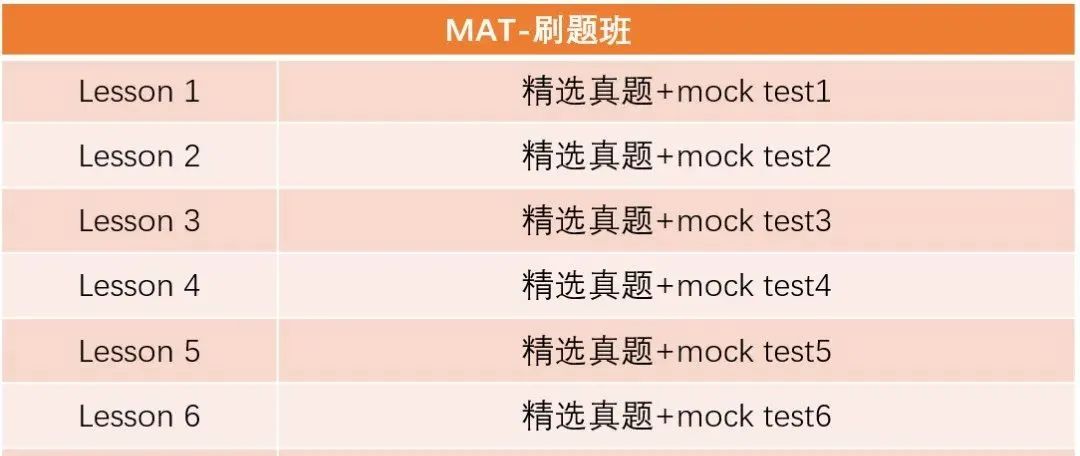
01MAT课表

02MAT课纲