有计划参加今年的AMC12的学生,从暑假开始就必须开始做备赛规划了。我近期将挑选几道AMC12真题做一些分析和点评,希望能对大家有所启发和思考。
上次我们选择的是一道计数问题(见《【AMC12题选】计数问题中的斐波那契数列》),这次我们选一道数论问题。题目如下:
224-1这个数,有多少个两位数的约数?
在分析题目以前,我先说说AMC12的题目编排特点。从历年的AMC12真题可以看出,每套试题基本上遵循难度递增的规律。
前10题属于基本题,原则上应该都能做。特别是前5题,一般喝着茶哼着小曲儿就完成了。
11~15题有一定难度,但通常不会难到无从下手,步骤也不会特别多,不会涉及很复杂的计算过程。这5道题是整个考试中最关键的部分,可谓“兵家必争之地”——如果能全部拿下,加上前10题的分数,二等奖的分数线和AIME的入围线都触手可及了。
16~20题的难度进一步增加。要么是需要用到不常用的知识点(例如高次多项式的性质),要么是不容易找到突破口、难以下手,要么是计算步骤很繁杂,很费时间和精神。总之,每道题的分数都浸透着血汗。
21~25题是真正的“猪骨头”,没有足够锋利的牙齿是很难啃得动的。如果信心不足的话,拿1.5分离开应该是比较明智的策略。
对上面的总结,我需要做两点说明。
1. 这个难度分析是针对至少有实力争取二等奖的学生而论。实力不足的学生在11~15题就已经撞上“铜墙铁壁”了。
2. 绝大部分题目是遵循上面的难度分级的,但与此同时,每套题目中都存在难度“错位”的题目。如果每5道题为一个难度档次,我们不时会在第二档次的位置上(例如第9题)遇上第三档次的难度,在第三档次的位置上(例如第13题)遇到第四档次的难度,以及与这两种情况相反的状况。还有相对罕见但还是有机会遇上的情况,就是第五档次的位置上出现第三档次难度的题目——我猜这是出题人跟考生玩的心理战,要的就是考完以后拼命拍大腿的效果。
现在回到我们今天要讨论的题目,它出现在第15题的位置。这是一个很敏感的位置。如果前面的题目做得顺利,这道题就是最后一个相对容易拿分的题目。同时,在这个位置上碰到棘手的题目的可能性也很大,所以容易产生患得患失的心理——既想顺利拿下分数,又担心耗费太多时间影响后面10道题的答题。
题目言简意赅,并没有过多的条件。求一个数的约数,可用的方法也不多,通常都是利用质因数分解,这是肯定会首先尝试的路径。要说这道题的难点,主要在于224-1这个数比较大,是一个八位数。我们可以合理猜测它的约数很多,那么要不遗漏地列举所有(两位数的)约数就有一定困难。
另外还有一个经常被忽略的考虑因素,就是解题时间。AMC12每道题的平均解答时间是3分钟,对于第15题这个位置的题目,解题时间通常要控制在5分钟以内。
综合来看,这道题虽然不需要复杂的分析,考的都是硬功夫,但有很多技术细节要处理。要在5分钟内完成解答,对学生的基本功和心理素质都是很大的考验。
下面具体说一下解答过程。由于要分解的数是以幂的形式表达,所以分解过程实际需要的是因式分解的方法。多次运用平方差公式可得
224-1=(23-1)(23+1)(26+1)(212+1).即
224-1=7×9×65×(212+1).现在还需要分解最后一项。根据立方和公式,
212+1=(24+1)(28-24+1)=17×241.因此,我们最终得到
224-1=32×5×7×13×17×241.
根据这个质因数分解式以及约数个数的计算公式可知224-1一共有96个约数。所幸我们只需要列出其中的两位数约数,关键在于不能遗漏。这就归结到计数方法了。
我们可以使用分类枚举的方式进行列举。由于241是三位数,所以我们只需考虑由3,5,7,13,17相乘得到的两位数约数。首先列举乘积中包含17的约数,一共有3个:
17, 17×3, 17×5.然后列举乘积中包含13(但不包含17)的约数,一共有4个:
13, 13×3, 13×5, 13×7.再列举乘积中包含7(但不包含13和17)的约数,一共有3个:
7×3,7×5,7×32.最后列举乘积中只包含3和5的约数,一共有2个:
3×5, 32×5.
所以224-1的两位数约数一共有12个。
最后总结一下。这道题不算难度很大的题目,考的都是硬基本功。题目本身是一个数论问题,但需要利用因式分解的方法得到质因数分解式,以及通过分类枚举的方式得到所有两位数的约数。也就是说,一道题目中融合了数论、代数和计数问题的知识点和方法。这类考察学生的综合能力的题目在数学竞赛中非常常见,但题目的设计也是很费心思的,优秀的题目不可多得。我认为这道题的设计就很精巧,值得我们多做回顾和思考。
顺着这道题的设计思路,我们很容易编出难度更大的题目,例如改一下需要分解的数的表达式、求三位数的约数等等。
最后,我再给一道与质因数分解有关的真题。题目如下:
对所有大于1的整数n,定义pow(n)为能整除n的最大质数的最大的幂。例如,pow(144)=pow(24×32)=32。使2010m整除下面的数的整数m最大是多少?
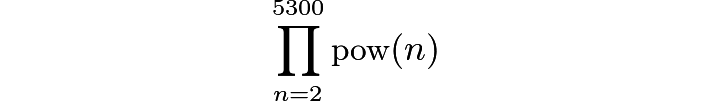
这道题出现在第25题的位置。几乎所有的第25题都很难,能在考试中做出第25题的学生可谓凤毛麟角。这道题看起来也确实吓人——虽然pow(n)的定义不算复杂(特别是题目中很贴心地举了个梨子),但要在短时间内并不容易“消化”透彻,因而也就不好做分析推理。
不过在我看来,这道题的难度应该介于第三档和第四档之间,换句话说,就是放在第三档题目中属于偏难的题目,而放在第四档题目中属于偏容易的题目。
话说回来,只要稍微有点难度的题目放到最后一题的位置上,都会对学生造成很大的压力。毕竟大脑已经高速运转了一个小时,剩下的时间都是以秒来计算,仍然能保持清醒冷静不慌乱的学生,必定都具备过人的能力。
暑假是开始备战AMC12的重要时段。因此,欧拉数学苑将在暑假期间安排一对一和小班的AMC12辅导课程。
其中,小班课程为3~4人规模,主要针对已经有参加AMC10的经验且AMC10的自测水平达到85分(考试成绩可以降低到75分)的学生,备考目标为AMC12的分数达到105~120的区间。
如果备考目标是120分以上,建议参加一对一的辅导课程。