有计划参加今年的AMC12的学生,从暑假开始就必须开始做备赛规划了。我近期将挑选几道AMC12真题做一些分析和点评,希望能对大家有所启发和思考。
我们在前三篇文章里分别选择了计数问题,数论问题以及多项式问题。本篇的题目如下:
设(a1, a2, …, a10)是从1到10这10个整数构成的一个序列,使得对任意2≤i≤10,ai+1和ai-1中至少有一个出现在ai前面的位置上。满足以上性质的序列一共有多少个?
在这个题目中,对序列的规则要求就只有一个,但这个规则的描述“有点绕”,我们很难迅速了解满足这个规则的序列应该呈现怎样的形式。
有少数题目的条件,如果直接按其当前的表述方式来使用是非常不方便的。此时,我们需要尝试换一种方便使用(且等价)的表述,或者把这个条件更深层次的本质挖掘出来,再运用到题目的解答之中。
无论是哪种做法,目的都是更深刻地理解题目的条件。达到这个目标的一个很重要的路径是“举例”,即构造几个满足条件的具体例子。
对这个题目,我们先假设取a1=1,则对照规则,a2只能取2。再进一步可知,a3只能取3。如此类推下去,每个位置上的取值都是唯一的,即以1开头的序列只有一个。
再假设取a1=3。此时a2可以取2或者4。如果取a2=4,a3可以取2或者5。如果取a2=2,a3可以取1或者4。
通过上面两个例子的构造过程,我们可以发现一个特点:每一项都是紧挨着前面已有的项(不一定是前一项)来取值,形成一个“不断(向左和向右)延伸”的取值模式。这个特性当然是由题目中设置的规则所决定的。
为了分析这个特性对于满足要求的序列的数量的影响,我们来分析a1=3的情形。3把其余的数“切割”成两组:{1, 2}, {4, 5, 6, 7, 8, 9, 10}。把这9个数安排在不同的位置上,使它们满足题目的规则要求。为此,我们要注意下面两个结论:
1. 同一组内的数有严格的前后位置关系。在前一组中,2的位置必须比1靠前;在后一组的所有数中,4的位置必须最靠前,5的位置必须比4的位置靠后,10的位置在整组中位于最后。
2. 不同组内的数的位置关系完全没有限制。比如2在前一组的数中位置最靠前,10在后一组的数中位置排在最后,但2在整个序列中的位置可以排在10后面,此时形成的具体序列是
3, 4, 5, 6, 7, 8, 9, 10, 2, 1.当然,我们还可以构造其他顺序的序列,例如
3, 4, 5, 2, 1, 6, 7, 8, 9, 10或
3, 4, 5, 2, 6, 7, 1, 8, 9, 10.
总之,就是把{2, 1}和{4, 5, 6, 7, 8, 9, 10}这两组数,在不破坏本组的排列顺序的情况下,组合成9项的序列。组合的不同方式数恰好是从9个对象中选择2个对象的组合数。
记从n个元素中取m个元素的不同方式的数量为C(n,m),则在本题中,以3开头的序列恰好有C(9,2)个。一般地,以k开头的序列恰好有C(9,k-1)个。例如,以1开头的序列有C(9,0)=1个。
因此,满足题目要求的所有序列按照排在第一位的数分类,从1到10共分成10类,每一类的数量依次为C(9,0), C(9,1), ..., C(9,9)。根据组合数的相关公式,这10个组合数的和恰好等于29,即512。
高中数学已经具有较高的抽象性,即使是一些基本概念和性质的理解,往往也需要借助简单和具体的例子才能理解得更透彻。数学表述虽然是严谨的,但我们只有了解清楚它所刻划的实际图景,才能知道怎样去使用相关的概念和性质。并且,通过对照数学表述和具体例子,也有助于我们更好地掌握数学语言的运用方法。
有举例子的意识,并且懂得举出有价值的例子,帮助自己更快更深刻地理解抽象的数学表述,是衡量数学能力的一个指标。下面再给另一道真题,供大家思考和练习:
设x和y是两个不相等的非零实数,且满足等式
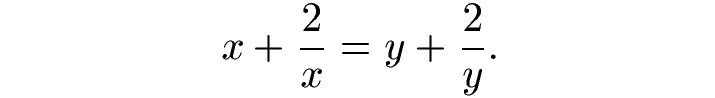
请问x和y的乘积是多少?
这道题跟方程有关,但不方便用常规的方程方法来解决。一方面,题目中只有一个等式,但有两个未知数;另一方面,题目并不要求确定每个未知数的值,而只需求它们的乘积。我们需要思考,怎样换一个角度来看待题目中的等式?