VCE中数（Math Methods）易错题目分析及高考答题建议

离2023 的VCE考试已经只剩不到3个月了，相信今年考试的同学们已经开始着手进行复习啦。今天我们就来看看VCE中数（Math Methods）一些比较容易扣分的“坑”，容易出错的题目和一些高考答题建议。

01、VCE 中数 - 函数和代数

函数和代数

VCE中数函数部分整个考试题目类型比较灵活，也属于难题比较多的，主要需要学生仔细分析隐藏的考点。比如，在考察二次方程的时候，一般不会直接问discriminant和roots的数量之间的关系，但可能会侧面的问“什么情况下这两个函数有两个交点/只有一个交点/不相交？” 所以需要注意，如果问到某个特征值数量相关的时候，优先考虑下判别。例如：

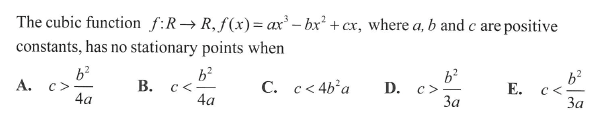
Solution：先求出导数后，利用f'（x）=0 的discriminant<0 可以得到选项D。

这部分一个特别常考但又很容易出错的考点是逆函数的定义域和值域 （域和反函数范围）。求逆函数本身并不复杂，很多学生习惯在求出反函数的表达式后，再根据表达式去计算它的值域和定义域，而这种方法是错误的 （可能偶尔会出现巧合刚好得到正确的答案）。正确的方法是利用

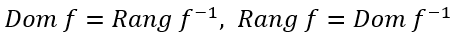
通过原函数的值域来确定。

另外一个经常会被忽略的易错点是三角函数方程求解（circular functions）。大家经常忽略三角函数的特点，很容易漏掉部分解。例如：

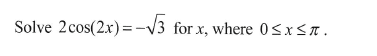
很多同学在计算时可以准确的到 cos（2x）=-/2，但忽略了这个值对应了 5/6 和7/6两个不同的值。利用单位圆可以知道除了 ±1，其他的正弦和余弦的值都会对应两个角度，同时在计算的时候，还要记住正弦/余弦函数是周期的，过程中最好带上2nπ，计算出最终答案后再根据定义域选择所有符合条件的。

02、VCE 中数 - 微积分

差异化和整合

这一部分首先特别需要注意的是答题的时候使用正确的数学符号，尤其是积分的时候不要忘记写末尾的“dx”。在计算不定积分（不定积分）的时候不要忘记在最后加上 “+c” （任意常量）。

在定积分（definite integral）部分，尤其是选择题中，一定要注意积分上下限。选项中经常会调换上下限来迷惑考生，这时候就需要利用

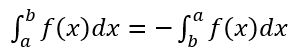
这部分比较容易出错的题目主要在积分的应用 – 计算面积。需要注意定积分（definite integral）算出来的是函数和x-axis之间的一个符号区域，也就是，这个计算出来的面积是带有符号的（如果函数在x轴以上是正，函数本身在x轴以下为负），在求两个不同函数之间的面积的时候也要注意一定是用上方的函数减去下方的（保证差值永远为正）。如果两个函数的大小关系发生变化就一定要分成不同区间进行计算。

比如17年中数的选择题，看似简单的套用公式，但实际错误率非常高，主要就是考生忽略了"面积"的符号以及积分上下限。考虑到signed area，B选项看似正确，但如果仔细观察，就会发现第二个积分应该是从b到c而非c到b，利用积分的性质化简我们会发现 D选项才是正确选项。

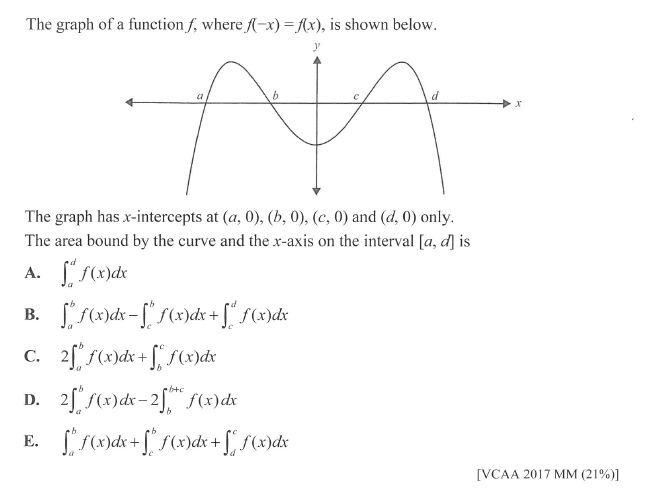
03、VCE 中数 - 概率 

discrete and continuous probability

概率部分比较考察学生的读题理解能力，通常题目比较长，需要学生能正确的把题目的信息转化为响应的数学表达，而这一个步骤通常是学生觉得比较困难的，通常后续的计算都可以套用公式比较简单。在答题过程中，注意如果使用了任何题目中没有出现的notation，一定要清楚明确的定义出来，比如“let A be the event that …”。在套用公式时也建议把对应的公式写出来再代入数字，以防过程中出现计算错误。

计算概率的题目中如果出现 P(X>a) 或者 P(Xa)的时候一定要注意到底是discrete还是continuous。在continuous的情况下，以上两个概率并没有区别，但如果是discrete，那么这两概率会不同 P(Xa)= P(X>a)+ P(X=a)。所以一定要注意审题，先确定好是discrete case 还是 continuous case。

Solution：题目中明确提到这是discrete rv，只可能为非负整数 （这也可以从probability function看出来：如果是continuous rv，那么Pr(X=k)一定为0，只有probability density function）。那么 Pr(X>1)=Pr(X2)=1-Pr(X=0)-Pr(X=1)，选项E 正确。

这部分另一个常考的易错点是关于density function 的性质，比如下图例题：

通过原函数的值域来确定。

Solution：从density function的性质可知 a+4b+0.2=0.8，同时

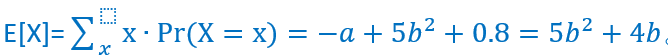
由于a，b都应该在0 和1之间，所以最大最小值分别是a=0 和b=0 的情况，选项E正确。

这类型题目中看起来题目中有未知的parameter，但实际上需要学生利用density function 积分为1 （continuous case）以及 求和为1（discrete case）的性质对题目中出现的参数先进行计算再加以利用。

在上述题目中，还有一个往往会被同学们忽略掉的隐藏条件 – 概率值一定在 [0, 1] 区间上，这也是经常可以帮助我们排除答案或者确定极值的重要条件。

这部分题目还需要特别注意题目问的到底是exact value还是approximation， 如果是approximated value一定要注意要求的精确度（d.p.），计算器上也要注意相应的设置。比如，如果题目要求精确值 （0.03125），但如果错误的设置成4dp，那么尽管可以除尽，计算器也会给出0.0313的“错误”答案。所以大家平时练习的时候需要熟悉计算器使用以及仔细读题。

04、答题习惯 

大家在平时练习的时候注意养成良好的答题习惯，注意以下几点：

1.  注意使用和题目一致的符号，比如题目要求  “f’(x) = “ ， 那么答案就不能写成 “ y= “

2.  对数函数（logarithm function）的表达中一定要清楚明确的写出底数（base）是多少，比如

3.  在求积分的题目中，牢记每一个积分符号最后都要有 “dx”；

4.  需要画图的题目，所有相关的重要的点都需要标记，比如 x-intercepts， y-intercepts，intersections，turning points， etc；

5.  书写工整清晰，包含必要的解题步骤 （试卷都是扫描阅卷，所以尽可能清晰整洁，字体大小适中）。

以上就是VCE中数里面，每年往往都有学生痛失宝贵分数的地方，希望大家通读的同时，在自己刷题的时候也要注意关注这些细节哦！