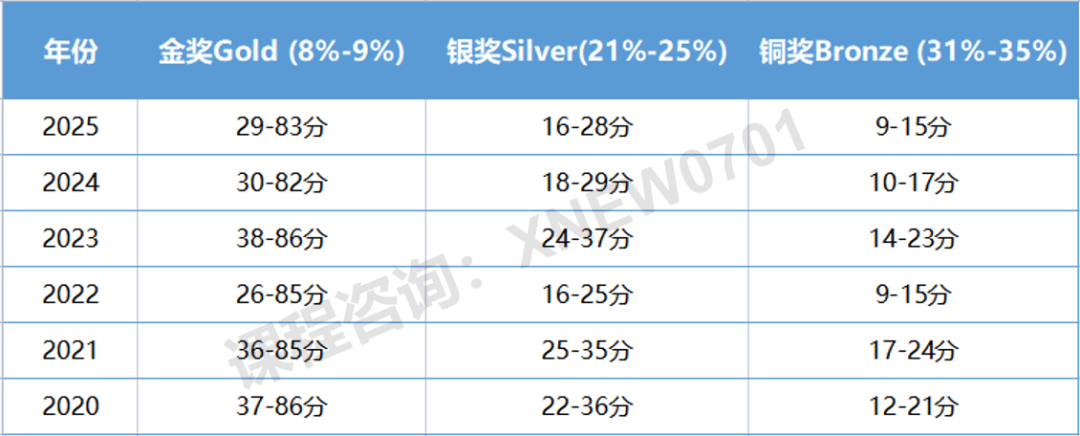
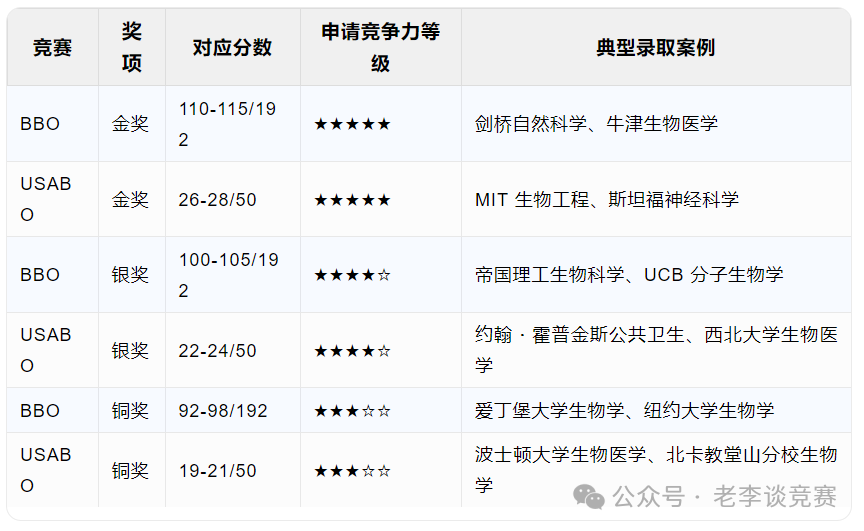
统计一词源于国情调查,一般来说包括三个含义:统计工作、统计资料和统计科学。其中统计工作是指的搜集、整理和分析客观事物总体数量方面的资料,统计资料则是由统计工作所获得的各项数字或文字资料,一般反映在图表、分析报告、统计年鉴里面,而统计科学则是指导统计工作的原理、原则和方法。
因此,在数学建模比赛中统计问题一定要有文献资源和数据资源的搜集,并且这一部分内容也要反映在论文中,而整理通常来说是将搜集到的资料以图表的形式呈现在论文中,最后分析自然就是数据预处理和统计算法建模求解。
1预测
预测,顾名思义,即根据先用数据规律推算接下来的数据。而预测按照算法可以分为四大类,一为回归分析,二为概率估计,三为时间序列,四为机器学习。
01回归分析
对于回归分析,该类算法适用于求解单一输出的问题,在某种程度上可以叫做函数拟合,即利用一种函数去逼近原有数据 。我们在高中阶段学习的线性回归就属于一种预测方法,下面给出几种函数类型:
多项式拟合: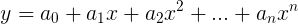
非线性拟合: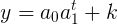
多元拟合: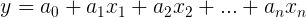
如下图所示,该图像是利用了非线性函数对原有数据进行了逼近,有了函数自然也就可以根据输入计算出接下来的数据,所以回归分析也只适用于单输出问题。而回归分析的关键问题就是对某一函数模型的参数进行求解,matlab中有专门的拟合工具箱polyfit和lsqcurvefit:
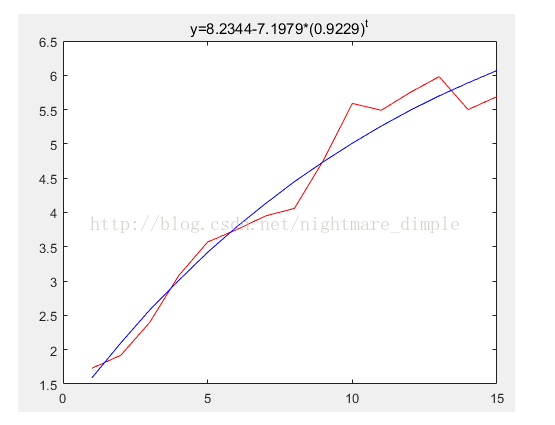
这里小编用MATLAB编了两种基础的回归分析程序。
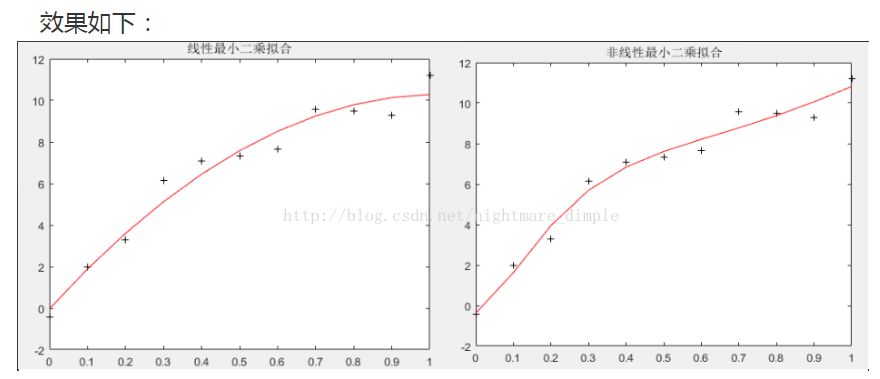
02、概率估计
而对于概率估计,其中的代表是马尔科夫链算法,即先给数据划分状态,然后将数据的分布规律用状态转移来解释。最后对于当时数据的状态,利用根据状态间的转移概率可以求得未来的状态概率分布,自然也能求得下一状态的预测值。
比方说,我只去A,B,C,D四个食堂吃饭,现在告诉你我吃饭的记录,现在就需要计算我在这四个食堂中的转移概率,如我去食堂A吃过后再去四个食堂吃饭的概率是多少?通过这些转移概率不断推算我下一个要去的食堂,再根据四个转移概率得到最大可能去的食堂。但是这只是离散问题的预测,对于连续问题,自然也就需要将连续数据划分为若干个离散的状态,在使用此方法。
此方法对于初学者来说掌握会比较困难,不过如果能成功使用会为论文添色不少,有兴趣的同学可以自行查找资料了解。(《数学建模算法与应用》一书上有讲解)
03、时间序列
第三类称其为时间序列,因为输入是按顺序的离散值,大多数情况下就是时间,针对此类问题,由于输入以稳定步长增长的,所以不用考虑输入,直接研究输出的变化规律,这一点类似于高中学的数列,比方说有名的斐波那契数组:1,1,2,3,5...,它的数据特征是f(n+2)=f(n)+f(n+1),现在我们要求后面的数就直接利用该数据特征就行了,当然也可以求出其通项公式,有兴趣的同学可以求着试试。
而时间序列方面的算法其实就是猜测数据前后存在着什么关系,比如说:一次移动平均算法就是猜测每一个数据 与最近的部分数据的均值存在着某种关系,指数平滑法就是猜测每个数据都跟之前的历史数据的加权平均存在着某种关系。这些算法都可以算作是时间序列算法,不过以上算法都是对数据特征简单的猜测,而对于更复杂的数据特征则可能会用到微分方程,利用微分方程,即可以直接预测,还能用于灰色系统,从而将无规则数据转化为有规律的生成序列。
04、机器学习
最后一个就是机器学习,即我们只需要搭好框架,数据特征则会由其自己挖掘,比较有名的有:支持向量机(SVM)、决策树、神经网络(深度学习)。这种算法的最终目的是模拟人脑的结构,它的好处就是在搭建好网络结构之后,通过对已有数据的学习,网络会自行提取数据特征,然后只要我们输入一个数据,网络将自行计算,然后输出它的预测值。这种方法的优点是方便,无需考虑数据规律和数据维度,而缺点则是要求数据量要大,少量样本的训练效果一般不具有适用性。
05、模型检验
预测问题中尤其还要注意的是对结果的检验,通常使用残差和后验误差等作为概率统计的检验,也可以用均方误差MSE检验。
残差值反映了预测值和原始数据的相对差距:
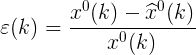
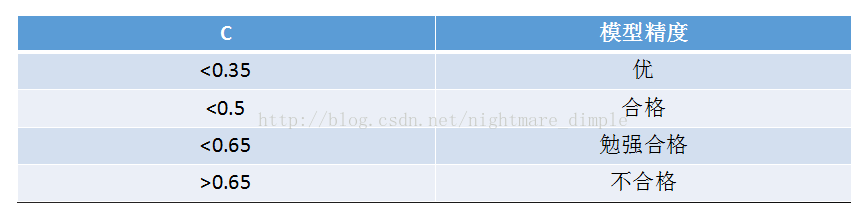
后验误差反映模型的精度:
![]()
![]()
然后依据下表判断模型精度:
均方误差则是一个简单的误差效果:
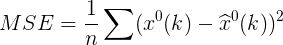
2、分类/聚类
首先要弄明白分类和聚类的区别:
分类(判别):数据包含数据特征部分和样本标签部分,分类的目的就是判别新的数据特征到其应有的样本标签(类别)中。
比方说,现在告诉大家一个教室里面其中一半人每个人的性别(男女),现在需要大家将另一半人中每个人的性别判断出来,因此大家首先要做的的找到区分性别的特征,然后应用到另一半人身上,将其归类。
聚类:数据中只有数据特征,需要根据某一标准将其划分到不同的类中。
同样的,现在一个教室里面所有人都没什么标签,现在需要你将整个教室的人分为两类,那么你可以从性别、体型、兴趣爱好、位置等等角度去分析。
可以看到,分类其实跟预测差不多,只不过输出是一维的,并且还是整数,所以可以用预测中的机器学习方法来解决分类问题。而聚类则不同,一般来说,聚类需要定义一种相似度或者距离,从而将相似或者距离近的样本归为一类,常见的有:kmeans算法、分层聚类、谱聚类等。
对于聚类来说,除了相似性的度量之外,还有一个比较重要的是终止条件,即需要聚成多少类,一般来说,基本都是在聚类之前就设定好需要聚成多少类,其中kmeans就是先设定几个类中心,然后将与类中心相近的数据归到那一类,然后不断更新类中心,直至所有数据聚类完毕,而分层聚类则是相反,先将所有数据各自为一类,然后将相似的类合并,直至达到k类为止...
当然,也可以将终止条件改为当最小的距离大于某一阈值时,不再合并类(适用于分层聚类),除了这些算法,还有机器学习方法,如:自组织竞争网络(SOM),可以自行了解。
接下来我们以分层聚类为例进行讲解,这一部分例子来自于《数学建模算法与应用》,用以辅助说明。通常来说,分层聚类有两类,一类是从上到下的分裂(即现将所有个体看做一个类,然后利用规则一步步的分裂成多个类),另一类是从下到上的合并(即先将每个个体看作一个类,然后依据规则一步步合并为一个类)。因此分层聚类最终可以得到一个金字塔结构,每一层都有不同的类别数量,我们可以选取需要的类别数量。
例子:设有5个销售员w1,w2,w3,w4,w5,他们的销售业绩由二维变量(v1,v2)描述:
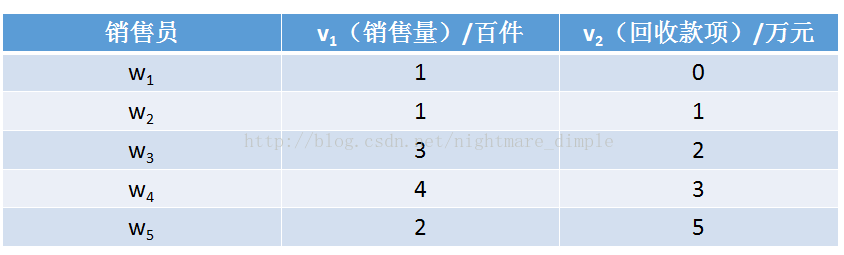
将5个人的两种数据看作他们的指标,首先,我们简单定义任意两组数据的距离为:
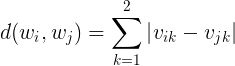
与此相对应的,当有样本归为一类后,我们要计算类间距离就又得需要一个计算方式,我们定义任意两类间的距离为两类中每组数据距离的最小值:
![]()
因此,可以得到任意两个销售员的数据距离矩阵:

Step1 首先,最相近的两组样本是w1和w2,他们的距离为1,所以先将其聚为一类;
Step2 然后,剩下的样本为{w1,w2},w3,w4,w5,我们发现除了距离1之外,最相似的是 w3,w4,他们的距离为2,所以将其聚为一类;
Step3 然后,剩下的样本为{w1,w2},{w3,w4},w5,我们发现除了距离1,2之外,最相似的 是{w1,w2}和{w3,w4},他们的距离以 w2和w3的距离为准,距离为3,所以将这两类聚为一类;
Step4 最后,剩下的样本为{w1,w2,w3,w4},w5,只剩最后两类了,所以最后一类为 {w1,w2,w3,w4,w5},类间距以w3/w4与w5的距离4为准。
用matlab编程结果如下:

转载自:CSDN