“水桶上方有一根水管,水流以一定速度流入水桶,同时水桶侧面有一小洞,水以另一速度流出水桶,请问装满水桶需要多长时间?”
小时候每当看到这种问题,我的第一反应总是想把这个桶掀翻,相信不少人应该会跟我有类似的反应。但当我们掀翻这个桶后,一个更令人沮丧的问题便会立刻浮出水面——我们为什么要学这个?这对我们的生活又有什么意义呢?
想到这里,可能不少生性敏感的同学已经陷入了焦虑的泥潭——因为我们可以逃避一个桶,但却不能逃避生活。当然你可以合理地怀疑这只不过是一些无聊的大人随意创造出来用来消耗学生过剩精力的题目,但不幸的事实是,长大之后我们依然会围绕着这个桶展开各种各样的研究。
我们不光需要关心水的流入流出速度,可能还需要考虑这个桶会不会裂,水的蒸发速度,以及会不会有人突然冲出来把桶踢翻,那时我们需要考虑的就不光是数学的问题,还需要考虑材料学,气象学以及犯罪心理学。
既然如此,这些不切实际的问题的现实意义又是什么呢?
面对这个棘手的问题,我们或许能从IBDP数学官方的指引(Mathematics: analysis and approaches guide )中得到些许启发。在指引中,批判性思考(critical thinking)无疑是被使用最多的关键词,字理行间无不透露着编者对学生能够具有批判思考能力这件事的渴望。
由此我们可以推断,锻炼批判性思考能力是学习数学的重要意义之一。
▍那么首先,批判性思考是什么呢?
相比于用冗长,令人乏味的文字去描述这个本来就具有多重含义的概念,不如来看看下面这个故事,或许我们能从中获得一些灵感。若干年前泰国的一则电视广告中,一个霸气外漏的老板娘在熙熙攘攘的菜市场中收租,过程中不断地对摊贩指指点点,甚至直接砸了其中一个摊贩的秤,而这一切都被路人拍了下来并发在了网上。
视频一出便被疯狂转载,一时舆论大哗,铺天盖地地开始讨伐这个女老板。画面一转,原来这个之前面露凶色的女老板一直在默默地帮助市场里的摊贩,砸了的秤其实是被摊主做了手脚的秤。
故事说到这里,相信大家已经对批判性思考的内涵、作用以及重要性有了初步的了解。类似的事情在我们每天的生活中无数次上演,如果我们可以多角度的看待问题,不被自己固有的意识所左右,就可以不被表面现象所迷惑,尽可能地接近事物的本质。
▍其次,如何提升批判性思考能力?
毕竟我们不能每天都靠泰国的公益广告来救济,不仅效率低,效果也不好。其实IBDP数学的指引中对这个问题也做了解答,我们可以参考以下图表:
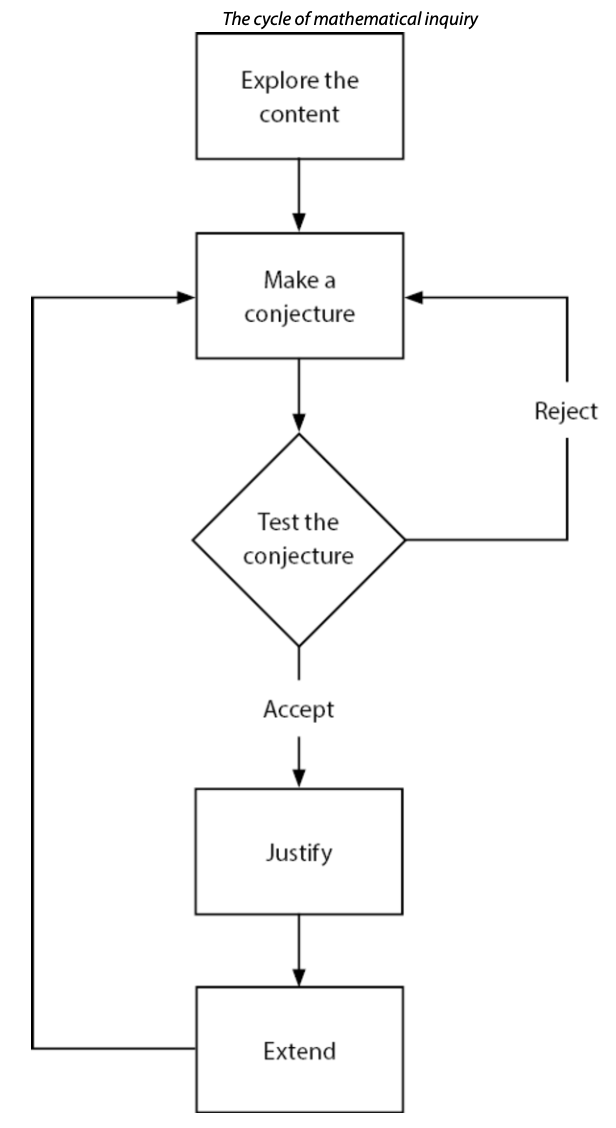
我们可以把它简单地总结为:大胆假设,小心求证,周而复始。
在这个图中,不断被提出来的假设和不断被扩充的知识形成了一个正向循环,知识的边界由此不断被扩大。数学能力和批判性思考能力亦如是,二者相辅相成,这也就解释了为什么那么多数学家都身兼数职,同时还是哲学家、思想家、科学家等等。
▍数学是其他学科的基础。就像好莱坞电影里外星人的通用语言总是英语一样,数学是其他学科的通用语言。
即便是对艺术类的学科,数学也有着其不可替代的作用。一方面,数学内在的可变性和所具有的创造性可以像永动机一样不断激发着人们的灵感,另一方面,不管是极具装饰性的巴洛克还是形式追随功能的包豪斯,其建筑设计、雕塑及各种衍生品都必须符合基本的数学物理原则,否则将无法实现,就像再骄傲的艺术家也不得不向地心引力妥协。
对其他自然科学和社会学科,数学的力量也被体现的淋漓尽致。例如不管是IBDP Math AA还是AI都会学到的微积分,我们可以用微积分来表示和研究事物的变化,不论是观测生物实验中菌群的增长速度,还是研究微观经济中某种产品的边际效益、边际成本,都可以用简单的微分公式被轻松得到。
▍此外,数学和其他科学的结合更是经常碰撞出让人啧啧称奇的发现,这些发现甚至经常让发现它们的科学家都感到不可思议。
发明平面直角坐标系的笛卡尔和费马,估计做梦也想不到这个沟通代数与几何联系的小东西,日后会对这个世界产生如此深远的影响。正是因为坐标系的发明,牛顿和莱布尼茨所才可以使微积分的观念逐渐成熟,使计算系统化,并把微积分地大面积使用到几何与物理中去。麦克斯韦就是依靠其深厚的微积分功底,把在实验中发现的定律转化为用微积分语言表述的方程,从而预测了电磁波的存在。
这一预测直接促使赫兹在1887年通过实验证明了电磁波的真实存在,十年后,特斯拉根据赫兹的实验结果建造了人类历史上第一个无线电通讯系统,五年后,马可尼发出了世界上第一封跨洋电报,至此,电视、手机等其他科学应用如雪片般纷至沓来。
这是人类在浩瀚宇宙中不断探索未知世界的一个缩影,当然在这一次又一次的波澜壮阔的探索中得到的成果,只靠数学自己是无法实现的,但是可以肯定的是,没有数学这个工具,这一切将不会发生。
▍最后回归到IB数学考试,多年的教学经验,我总结出最重要的一条原则:技术不能在凌驾于逻辑概念之上。
我们很多同学可以很快的求出微分、积分,但对这些所求得的微分积分的意义并没有完全理解,而这一点正是IBDP数学考试的重点。从往年的past paper中我们可以很清楚地看到,IBDP数学更多要求的是对概念逻辑的多角度,多层次理解,并不是怎么又快又好的解出一个复杂的函数。
对于这一点,需要我们在做题的时候不能依靠惯性,在做每一步的时候都想一下这么目的是什么,为什么要这么做,为了实现这个目的还有没有别的途径和方法,这些方法中哪个是最好的,这些方法之间本质的差别是什么。
对于更进阶的学生,我们甚至可以去思考一下假设题目中的问题和条件发生互换会发生什么情况,题目还可不可以做,如果不可以的话其原因又是什么。相信大家如果可以长期这样的训练自己,数学水平会有不小的进步。