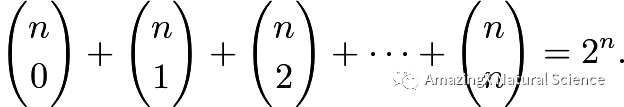作为AIME晋级赛之一,AMC10/12竞赛向来备受初高中考生关注。AMC10/12备赛倒计时只剩3个月不到,同学们要抓紧学起来!
AMC美国数学竞赛
AMC是由美国数学协会举办的美国数学竞赛。作为美国国家队的唯一选拔平台,每年仅北美地区就有超多30万次学生报名参加。
从小学到高中,全球有近几十个国家和3000所学校的学生角逐于这场竞赛。可以说无论是参赛人数、范围还是年龄,AMC比其他数学竞赛更具流行性和权威性。

AMC10适合学生:
针对10年级及以下且17.5岁以下学生的数学测试,建议8-10年级学生首选。
AMC12适合学生:
针对12年级及以下且19.5岁以下的学生的数学测验,建议10年级学生首选。
AMC10/12报名截止日期:
A卷:2023年10月30日9:00
B卷:2023年11月5日9:00
AMC10/12准考证下载:
A卷:2023年11月5日10:00至考试开始前
B卷:2023年11月11日10:00至考试开始前
AMC10/12赛事时间:
A卷:2023年11月9日
B卷:2023年11月15日
官方网站:https://www.maa.org/math-competitions
奖项设置:
全球个人奖项:
满分奖Perfect Score:获得满分150 分
全球卓越奖Distinction Honor Roll:全球成绩排名前1%
全球优秀奖Honor Roll:全球排名前5%
全球荣誉奖Achievement Roll:8 年级及以下年级在AMC10 中获得90 分以上
AMC必备公式
01、Geometry
Angles
Acute Angle: Angle measures less than 90 degrees
Right Angle: Angle measure that is 90 degrees
Obtuse Angle: Angle measure that is greater than 90 degrees
Straight Angle: Angle that is 180 degrees
Complementary Angles: Two angles that up to 90 degrees
Supplementary Angles: Two angles that add up to 180 degrees
Transversals and Parallel Lines with Angles
If there are two parallel lines, and they are cut by a transversal (just a line interesting both of the parallel lines), then the alternate interior angles are congruent.
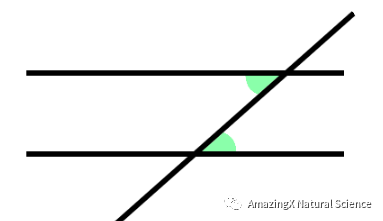
If two parallel lines are cut by a transversal, then corresponding angles are congruent.
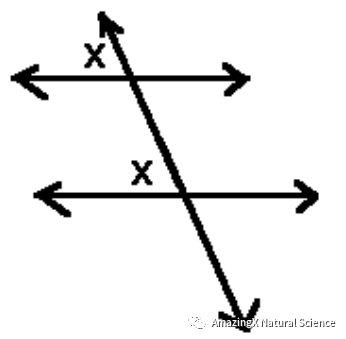
(In this diagram above, both of the angles that have X in them are congruent and have the same angle measure)
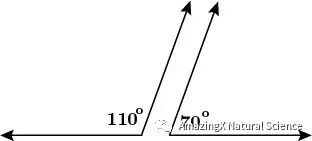
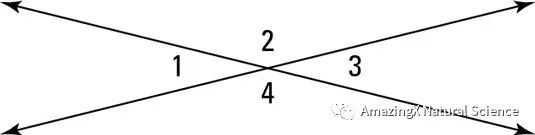
If two lines intersect, then vertical angles will be congruent.
In the diagram below, angle 1 is congruent to angle 3 while angle 2 is congruent to angle 4.
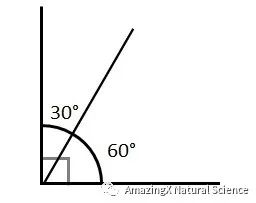
Special Right Triangles
30-60-90 Right Triangles
45-45-90 Right Triangles
Angles in ANY Polygon
The sum of the interior angles of any polygon is (n-2) x 180.
The sum of the exterior angles of ANY shape is 360 degrees. The formula to find the exterior angle of a REGULAR polygon is 360/n. (N represents the number of shapes.)
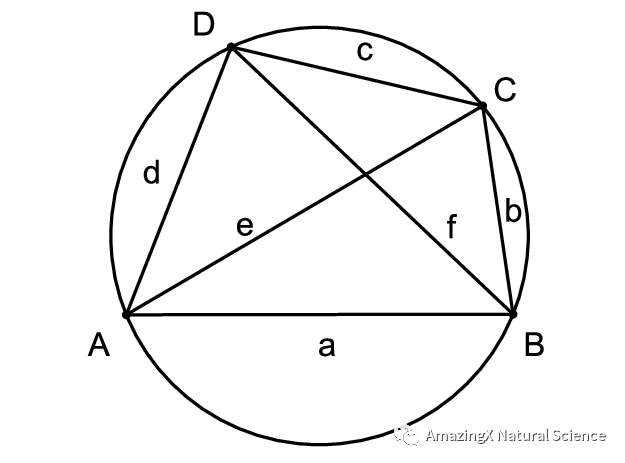
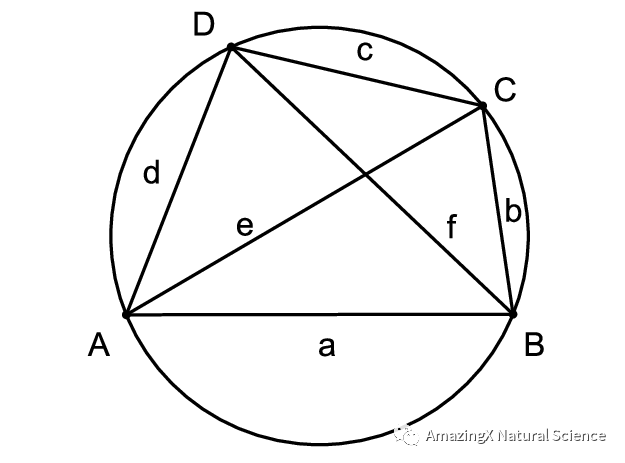
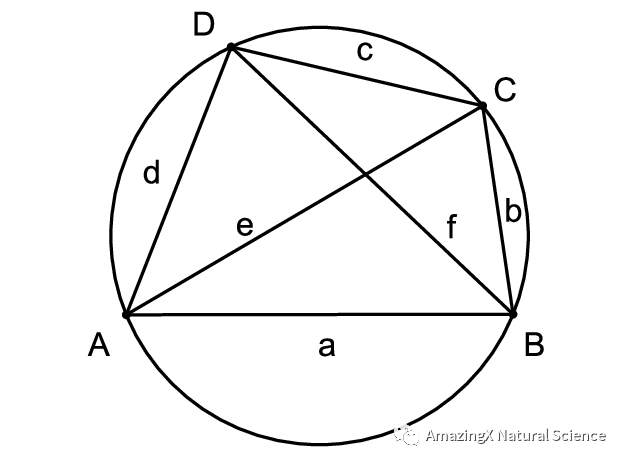
Ptolemy’s Theorem
Ptolemy’s Theorem states that if you multiply the diagonals, then that will be equivalent to the sum of the multiplication of the opposite sides. If you don’t understand what I mean, then the picture and example below should help you understand it.
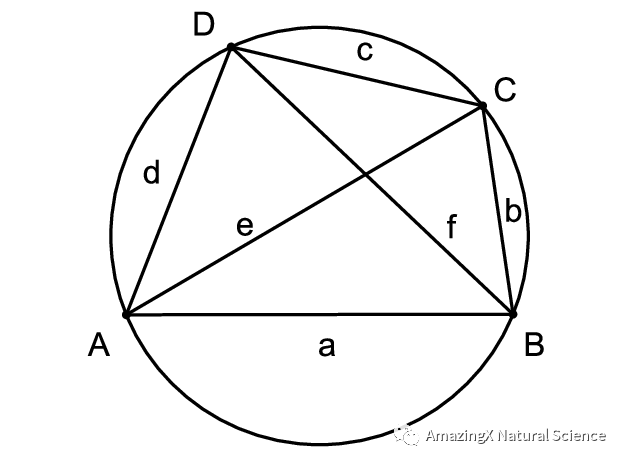
E x F = (C x A) + (B x D)
02、Ptolemy’s Theorem states that if you multiply the diagonals, then that will be equivalent to the sum of the multiplication of the opposite sides. If you don’t understand what I mean, then the picture and example below should help you understand it.
Algebra
Vieta’s Formula
Vietas is a great way to find the sum of the roots or the multiplication of it. In any polynomial that is in the form of ax2+bx+c, Vieta says that the sum of the roots is -b/a. The multiplication of the roots in this polynomial is just c/a. (Don’t forget that in vietas you don’t include the variables. You just use coefficients.)
Polynomial Remainder Theorem
If you have any polynomial f(x), and you’re dividing it by x-a, then the remainder can be found by replacing the variable x with the value of a throughout the entire polynomial. If that expression is equivalent to 0, then the polynomial is indeed divisible by x-a.
Conjugate Root Theorem
The AMC 10 kids can ignore this short section of conjugate roots if they want.
Theorem: If a polynomial p(x) that only has real number coefficients has a root of a+bi, then a-bi is also a root of that same polynomial. This can be extremely useful if you have a complex number root given in a polynomial.
Quadratics
The quadratic formula is usually used when you have an equation in the form ax2+bx+c.
The formula above can help you factoring a quadratic. However, remember that sometimes you might see quartic polynomials that might be in the form ax4+bx2+c. The clever way of factoring that is to substitute x2 with another variable. Pretend that variable is y. After you do so, you get ay2+bx2+c.
Geometric Sequences
A geometric sequence has a property that for any two consecutive terms, the ratios of the numbers will always be the same. An example is 2, 4, 8, 16, 32. As you can see, the numbers are multiplying by 2.
In a geometric sequence, if the first term is a and the common ratio is r, then the nth term of the sequence is arn-1.
If you have to use algebra in your geometric sequence, then a way to label the terms is a, ar, ar2, ar3, etc. On the left, a represents the first term while r represents the number you multiply by.
The sum of a geometric series is in the picture below.
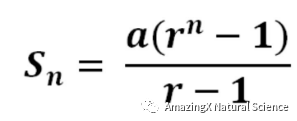
03
Number Theory
Euclidean Algorithm
If you’re asked to find the GCD (Greatest Common Divisor) or two numbers like 2 and 4, then you’re easily gonna say 2. However, what if the numbers are huge? That’s when this algorithm will help.
Pretend I have two numbers a and b in which a is less than b. THe GCD of (a, b) is equivalent to (a, b-a). You keep subtracting the numbers.
Pretend you want to find the GCD of 48 and 880. The Euclidean Algorithm states that the GCD of those two numbers is equivalent to (48, 880-48) which is equivalent to (48, 832). Instead of just subarcting this again and again, we can simply divide and use the remainder. If you divide 880 and 48, you get 18 with a remainder of 16. You disregard the 18 and only use the remainder. You then find the GCD of the remainder and the divisor which was 48 in this case. Now we need to find the GCD of 16 and 48 which is obviously 16.
Modular Arithmetic Basics
People sometimes get confused by the word mod, but it’s time to clear it up. When you say 8 is divisible by 4, you can simply say 8 = 0 (mod 4). All this means is that when 8 is divisible by 4, the remainder is 0. For example, 4, 8, 12, 16, 20, 24 are all 0 in mod 4. This means that when you divide all of those numbers by 4, you always get a remainder of 0. (The equal sign that i’m using actually has another line below it like in the picture below.)
Euler’s Totient Theorem
If we have a number a and we’re dividing it by n, and a and n are both relatively prime, then
a φ(n)1 (mod n). The φ(n)can be calculated using the euler totient function which is included in the handout.
04
Probability and Combinations
Formula for Permutations and Combinations

Pascal’s Identity

The image above is an important identity to know because it can help you in simplifying combinatorial expressions in a short amount of time.
Hockey Stick Identity

You should absolutely memorize this theorem because in some problems, you’ll have a lot of combinatorial expressions. Computing them will take a long time. Knowing this identity will make it super fast.
Vandermonde’s Identity
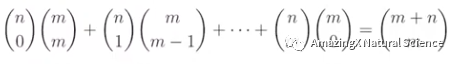
Sum of a Row in Pascal’s Triangle
This is something very important to remember since it can make your computation a lot easier.