你希望通过几种常见算法的实现,了解python在数学建模中的能力。
python除了丰富的原生数据结构外,拥有强大的第三方软件包支持,例如矩阵运算库Numpy,数据处理库Pandas、机器学习库Sklearn、深度学习库Tenserflow&Pytorch、科学计算库Scipy、图形绘制库matplotlib、网络算法库Networkx。此外几乎针对任何领域,都有第三方软件包的支持,这归功于python优秀的社区。使用者需要使用好pip这一软件包管理工具,发掘前人造好的轮子,尽量减少自己编程的难度。我们将在后面的问题讨论中介绍以下几种常用数学建模算法的python实现:
4.单源多宿最短路算法
我们的重点在于代码实现而非数学推导
1.数据拟合算法
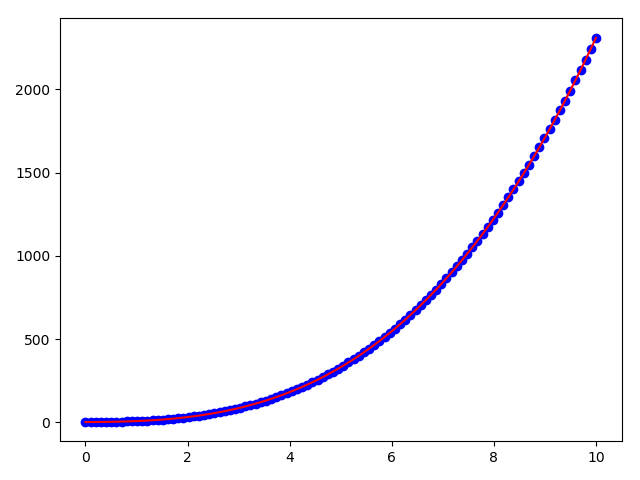
我们这里介绍通过最小二乘法拟合线性函数
-
#我们使用最小二乘法拟合一个三次函数,选取了5个参数 -
import numpy as np -
import matplotlib.pyplot as plt -
SAMPLE_NUM = 100 -
M = 5 -
x = np.arange(0, SAMPLE_NUM).reshape(SAMPLE_NUM, 1) / (SAMPLE_NUM - 1) * 10 -
y = 2*x3+3*x2+x+1 -
plt.plot(x, y, 'bo') -
X = x -
for i in range(2, M + 1): -
X = np.column_stack((X, pow(x, i))) -
X = np.insert(X, 0, [1], 1) -
W=np.linalg.inv((X.T.dot(X))).dot(X.T).dot(y) -
y_estimate = X.dot(W) -
plt.plot(x, y_estimate, 'r') -
plt.show()
-
import numpy as np -
from scipy import interpolate -
import pylab as pl -
x=np.linspace(0,10,11) -
y=2*x3+3*x2+x+1 -
xInset=np.linspace(0,10,101) -
pl.plot(x,y,"ro") -
for kind in["nearest","zero","slinear","quadratic","cubic"]: -
f=interpolate.interp1d(x,y,kind=kind) -
y_estimate=f(xInset) -
pl.plot(xInset,y_estimate,label=str(kind)) -
pl.legend(loc="lower right") -
pl.show()

-
import numpy as np -
from scipy.optimize import minimize -
def func(x): -
return(2*x[0]*x[1]+2*x[0]-x[0]2+2*x[1]2+np.sin(x[0])) -
cons=({"type":"eq","fun":lambda x:np.array([x[0]3-x[1]]),"jac":lambda x:np.array([3*(x[0]2),-1.0])},{"type":"ineq","fun":lambda x:np.array([x[1]-1]),"jac":lambda x:np.array([0,1])})#定义函数的多个约束条件 -
res=minimize(func,[-1.0,1.0],constraints=cons,method="SLSQP",options={"disp":True}) -
print(res)

-
classDisNode: -
def __init__(self,node,dis): -
self.node=node -
self.dis=dis -
def __lt__(self, other): -
return self.dis<other.dis -
classDisPath: -
def __init__(self,end): -
self.end=end -
self.path=[self.end] -
self.dis=0 -
def __str__(self): -
nodes=self.path.copy() -
return"->".join(list(map(str,nodes)))+" "+str(self.dis) -
classHeap: -
def __init__(self): -
self.size=0 -
self.maxsize=10000 -
self.elements=[0]*(self.maxsize+1) -
def isEmpty(self): -
return self.size==0 -
def insert(self,value): -
if self.isEmpty(): -
self.elements[1]=value -
else: -
index=self.size+1 -
while(index!=1and value<self.elements[index//2]): -
self.elements[index]=self.elements[index//2] -
index=index//2 -
self.elements[index]=value -
self.size+=1 -
def pop(self): -
deleteElement=self.elements[1] -
self.elements[1]=self.elements[self.size] -
self.size-=1 -
temp=self.elements[1] -
parent,child=1,2 -
while(child<=self.size): -
if child<self.size and self.elements[child]>self.elements[child+1]: -
child+=1 -
if temp<self.elements[child]: -
break -
else: -
self.elements[parent]=self.elements[child] -
parent=child -
child*=2 -
self.elements[parent]=temp -
return deleteElement -
defDijkstraWithHeap(nodes,start,GetNeighbors): -
dis=defaultdict(int) -
paths=defaultdict(DisPath) -
heap=Heap() -
visit=set() -
for node in nodes: -
dis[node]=sys.maxsize -
paths[node]=DisPath(node) -
dis[start]=0 -
heap.insert(DisNode(start,0)) -
while(not heap.isEmpty()): -
now=heap.pop().node -
if now in visit: -
continue -
visit.add(now) -
paths[now].dis=dis[now] -
for edge inGetNeighbors(now): -
end=edge.End -
if dis[now]+edge.value<dis[end]: -
dis[end]=dis[now]+edge.value -
paths[end].path=paths[now].path+[end] -
heap.insert(DisNode(end,dis[end])) -
return paths













